24.

Ako su kod dva trougla dve strane jednog jednake dvema stranama drugog, i to odgovarajućim, i ugao prvog, koji obrazuju strane jednake stranama drugog, veći od takvog ugla drugog trougla, onda je osnovica prvog veća od osnovice drugog.

Neka su ABG i DEZ dva trougla sa dve strane AB, AG, koje su jednake stranama DE i DZ, i to odgovarajućim, naime AB jednako DE i AG jednako DZ, a ugao kod A je veći od ugla kod D. Tvrdim da je osnovica BG veća od osnovice EZ.

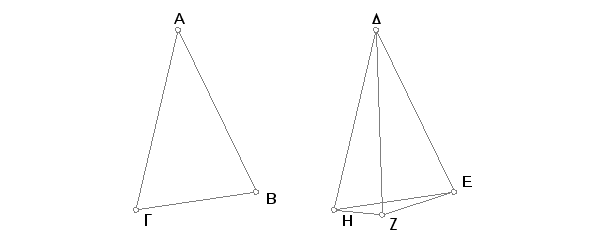
Pošto je ugao BAG veći od ugla EDZ, konstruiše se na pravoj DE u datoj tački D na njoj ugao EH jednak uglu BAG [I. 23] i prenese se DH jednako AG ili DZ, i povuku se EH i ZH.
Pošto je AB jednako DE, a AG jednako DH, a to znači da su dve strane BA, AG jednake dvema stranama ED, DH, i to odgovarajućim, i ugao BAG jednak uglu EDH, to je osnovica BG jednaka osnovici EH [I. 4]. S druge strane, pošto je DZ jednako DH, ugao DHZ jednak je uglu DZH [I. 5]. Stoga je ugao DZH veći od ugla EHZ, a tim pre ugao EZH veći od ugla EHZ. I pošto je u trouglu EZH ugao EZH veći od ugla EHZ, a spram većeg ugla nalazi se veća strana [I. 19], to će strana EH biti veća od EZ. Ali je EH jednako BG, pa će i BG biti veće od EZ.
Dakle, ako su kod dva trougla dve strane jednog jednake dvema stranama drugog, i to odgovarajućim, i ugao prvog, koji obrazuju strane jednake stranama drugog, veći od takvog ugla drugog trougla, onda je osnovica prvog veća od osnovice drugog. A to je trebalo dokazati.