21.

Ako se u unutrašnjosti trougla iz krajnjih tačaka jedne njegove strane povuku dve prave koje se seku, zbir povučenih pravih biće manji od dveju ostalih strana trougla, a ugao, koji one grade, veći.

U trouglu ABG su na jednoj strani BG iz njenih krajeva B, G povučene dve prave BD, DG, koje se seku. Tvrdim da je zbir BD i DG manji od zbira dveju ostalih strana trougla BA i AG, a ugao BDG je većo od ugla BAG.

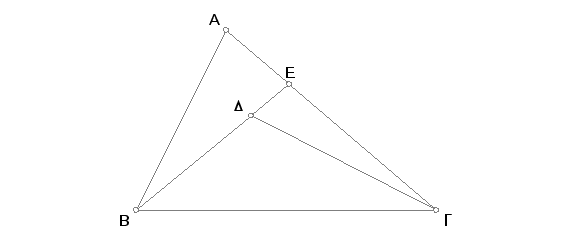
Produžimo BD do E. I pošto je u svakom trouglu zbir dveju strana veći od treće [I. 20], to je i u trouglu ABE zbir dveju strana AB i AE veći od treće. Ako se doda ista duž EG, zbir BA i AG biće veći od zbira BE i EG. S druge strane, pošto je u trouglu GED zbir dveju strana GE i ED veći od treće GD, to je, posle dodavanja iste dužine DB, zbir GE i EB veći od zbira GD i DB. A dokazano je da je zbir BA i AG veći od zbira BE i EG. Tim pre je zbir BA i AG veći od zbira BD i D G.
Dalje, pošto je u svakom trouglu spljašnji ugao veći od nesusednog unutrašnjeg [I. 16], to je i u trouglu GDE spoljašnji, ugao BDG veći od GED. Zbog toga je i u trouglu ABE spoljašnji ugao GEB veći od ugla BAG. Ali je dokazano da je ugao BDG veći od ugla GEB. Tim pre je ugao BDG veći od ugla BAG.
Dakle, ako se u unutrašnjosti trougla iz krajnjih tačaka jedne njegove strane povuku dve prave koje se seku, zbir povučenih pravih biće manji od dve ostale strane trougla, a ugao, koji one grade, je veći. A to je trebalo dokazati.