20.

U svakom trouglu zbir dveju strana, proizvoljno izabranih, veći je od treće strane.

Neka je ABG trougao. Tvrdim da je u trouglu ABG zbir dveju strana, proizvoljno izabranih, veći od treće, naime BA, AG od BG i AB, BG od AG i BG, GA od AB.

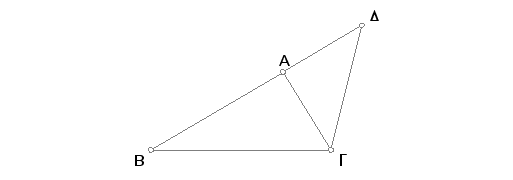
Neka se produži BA do tačke D, prenese se AD jednako GA i povuče se DG.
Pošto je DA jednako AG, ugao ADG je jednak uglu AGD [I. 5]. Tada je ugao BGD veći od ugla ADG [A. 5]; i pošto je DGB trougao, koji ima ugao BGD veći od ugla BDG, spram većeg ugla ležaće veća strana [I. 19], i zbog toga je DB veće od BG. Ali DA je jednako AG, pa prema tome su BA, AG veće od BG. Slično se dokazuje da su AB, BG veće od GA, a BG, GA od AB.
U svakom trouglu zbir dveju strana, proizvoljno izabranih, veće je od treće strane. A to je trebalo dokazati.