16.

U svakom trouglu je spoljašnji ugao, obrazovan produženjem jedne strane, veći od svakog od dva unutrašnja nesusedna ugla.

Neka je ABG trougao; produži se jedna njegova strana BG do D. Tvrdim da je spoljašnji ugao AGD veći od svakog od dva unutrašnja nesusedna ugla GBA i BAG.

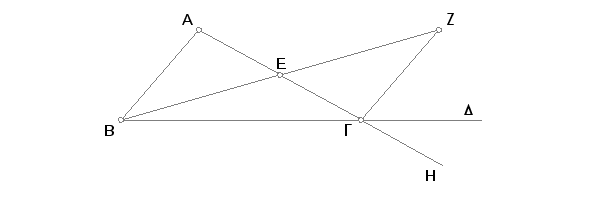
Prepolovi se AG tačkom E [I. 10], pa se povučena prava BE produži pravolinijski do Z, prenese se EZ jednako BE [I. 3], i povuče ZG [Post. 1], pa se produži AG do H [Post. 2].
Pošto je AE jednako EG, a BE jednako EZ, to su dve strane AE, EB jednake dvema stranama GE, EZ, i to odgovarajućim; i ugao AEB jednak uglu ZEG, kao unakrsni [I. 15]. Stoga je osnovica AB jednaka osnovici ZG, i trougao ABE jednak trouglu ZEG, i ostali uglovi su jednaki ostalim uglovima, i to odgovarajućim, koji su spram jednakih strana [I. 4]. Prema tome je ugao BAE jednak uglu EGZ.
Ali ugao EGD je veći od ugla EGZ [A. 5], te je i ugao AGD veći od ugla BAE. Slično se, polovljenjem BG, dokazuje da je ugao BGH, a to znači u ugao AGD [I. 15], veći od ugla ABG.
Dakle; u svakom trouglu je spoljašnji ugao, obrazovan produženjem jedne strane, veći od svakog od dva unutrašnja nesusedna ugla. A to je trebalo dokazati.