15.
Ako se dve prave seku, one obrazuju unakrsne uglove, koji su jednaki jedan drugome.
Neka se dve prave AB, GD seku u tački E. Tvrdim da je ugao AEG jednak uglu DEB i ugao GEB jednak uglu AED.
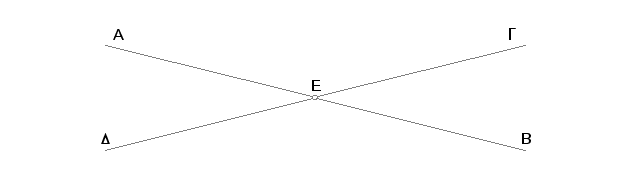
Pošto prava AE, podignuta nad pravom GD, gradi uglove GEA, AED, ti su uglovi zajedno jednaki dvama pravim uglovima [I. 13]. S druge strane, pošto prava DE podignuta nad pravom AB gradi uglove AED, DEB, ti su uglovi zajedno jednaki dvama pravim uglovima [I. 13]. Kako je ranije pokazano i uglovi GEA, AED su zajedno jednaki dvama pravim uglovima, pa su prema tome uglovi GEA, AEG jednaki uglovima AED, DEB [Post. 4, A. 1]. Kad se oduzme zajednički ugao AED, biće ostatak - ugao GEA - jednak ostatku - uglu BED [A. 3]. Na sličan način se dokazuje da su i uglovi GEB, DEA jednaki.
Tako, ako se dve prave seku, one obrazuju unakrsne uglove, koji su jednaki jedan drugome. A to je trebalo dokazati.
(Zaključak. Iz prethodnog je jasno da, ako se dve prave seku, one grade kod tačke preseka uglove, koji zajedno obrazuju četiri prava ugla.)