14.
Ako ma sa kojom pravom, u istoj tački na njoj, dve druge prave sa različitih strana prve prave grade susedne uglove, koji zajedno obrazuju dva prava ugla, te dve prave moraju se nalaziti u istoj pravoj.
Neka ma kod koje prave AB dve druge prave BG, BD, povučene iz iste tačke B, no ne sa iste strane prave AB, grade susedne uglove ABG, ABD koji zajedno obrazuju dva prava ugla. Tvrdim da su GB i BD u istoj pravoj.
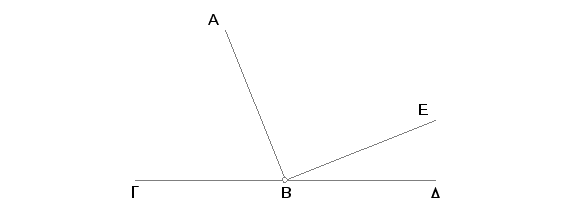
Ako se prava BD ne nalazi u pravoj BG, neka se prava BE nalazi u pravoj GB.
Pošto je tada prava AB podignuta nad pravom GBE, uglovi ABG, ABE obrazuju zajedno dva prava ugla [I. 13]; ali i uglovi ABG, ABD sačinjavaju dva prava ugla. Prema tome su uglovi GBA, ABE jednaki uglovima GBA, ABD [Post. 4, A. 1]. Ako se pak oduzme zajednički ugao GBA biće ostatak ABE jednak ostatku ABD [A. 3], manji - većem, a to je nemoguće. Dakle BE ne pripada pravoj GB. Slično se može dokazati da ne postoji nikakva druga prava sem BD. Prema tome su GB i BD u istoj pravoj.
Tako, ako ma kod koje prave, kod iste tačke na njoj, dve prave sa različitih strana prve prave grade susedne uglove, koji zajedno obrazuju dva prava ugla, onda se moraju te dve prave nalaziti u istoj pravoj. A to je trebalo dokazati.