12.

Povući pravu liniju normalno na datu beskrajnu pravu iz date tačke koja ne pripada datoj pravoj.

Neka je data beskrajna prava AB i data tačka G koja ne pripada toj pravoj; treba povući pravu liniju normalno na datu beskrajnu pravu AB iz date tačke G, koja ne pripada datoj pravoj.

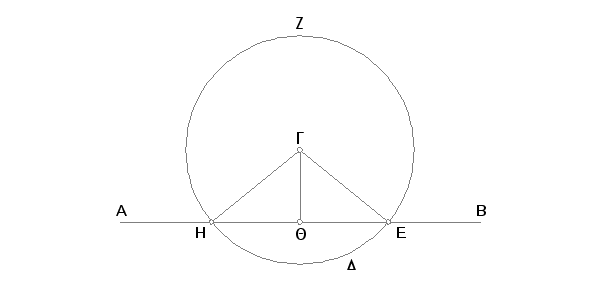
Uzme se sa druge strane prave AB proizvoljna tačka D, i sa središtem u G i rastojanjem GD nacrta krug EZH [Post. 3], pa se prepolovi duž EH tačkom Q [I. 10] i povuku prave GH, GQ, GE [Post. 1]. Tvrdim da je GQ normala na datoj beskrajnoj pravoj AB iz date tačke G, koja ne pripada njoj.
Pošto je HQ jednako QE, a QG je zajedničko, dve strane HQ, QG jednake stranama EQ, QG i to odgovarajućim, i osnovica GH jednaka osnovici GE; to je ugao GQH jednak uglu EQG [I. 8], i oni su pri tome uporedni. Pa ako prava podignuta na drugoj pravoj obrazuje sa njom međusobno jednake uporedne uglove, svaki od tih uglova je prav, a podignuta prava se zove normala na onoj na kojoj je podignuta [Def. 10].
Dakle prava GQ je normala na datoj beskrajnoj pravoj AB iz date tačke G, koja ne pripada datoj pravoj. A to je trebalo izvesti.