11.
Iz date tačke na datoj pravoj povući pravu pod pravim uglom prema datoj pravoj.
Neka je data prava linija AB i na njoj data tačka G. Treba iz tačke G povući pravu pod pravim uglom prema pravoj AB.
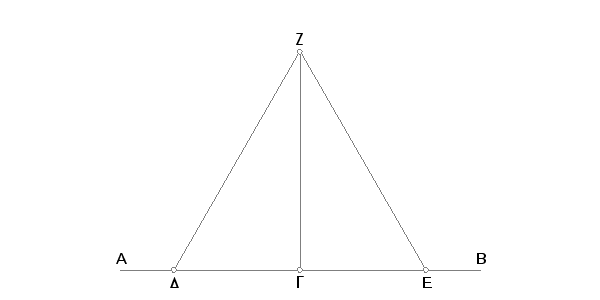
Uzima se na AG proizvoljna tačka D, pa se prenese GE jednako GD [I. 3] konstruiše se na DE jednakostran trougao ZDE [I. 1] i povuče se ZG. Tvrdim da je ZG prava linija, koja je pod pravim uglom prema datoj pravoj AB i prolazi kroz tačku G datu na njoj.
Pošto je DG jednako GE, a GZ je zajednička strana, to su dve strane DG, GZ jednake dvema stranama EG, GZ, i to odgovarajućim, i osnovica DZ jednaka je osnovici ZE, te je ugao DGZ jednak uglu EGZ [I. 8] i pri tome su oni uporedni. Ako pak prava, koja stoji na datoj pravoj tako da obrazuje uporedne uglove jednake jedan drugome, tada je svaki od njih prav [Def. 10]. Prema tome je prav svaki od uglova DGZ i ZGE.
Na ovaj način iz date tačke G na datoj pravoj AB povučena je prava pod pravim uglom prema datoj pravoj. A to je trebalo izvesti.