Пример језика за рад са функцијама

Поставка проблема
Парсер
Интерпретација
Синтаксно стабло
Додатак (shift и reduce акције)
- Разрешавање конфликата

У наставку ће бити представљен задатак какав се може наћи на испитним роковима. Циљ овог примера је да се покаже неколико кључних ствари које нису покривене у претходном разговору о синтаксним стаблима. То су:

рад са кориснички дефинисаним (непримитивним) типовима

истицање разлике између интерпретирања и формирања синтаксних стабала у акцијама у Bison-у (овде је она суптилнија него раније)

решавање нових shift/reduce конфликата у граматикама

Ради лакшег праћења, кодови се могу наћи на GitHub репозиторијуму.

Поставка проблема

Дат је програмски језик за рад са функцијама на следећи начин:

на располагању су константе функције, идентичка функција, sin, cos и све које се могу добити њиховом композицијом и основним аритметичким операцијама (изрази попут sin(x), cos(x), x, x + sin(x * x), cos(sin(x)) * cos(2 + x), приметимо да x представља идентичку функцију)
функције се могу чувати и доделити променљивама (наредбе попут f = sin(x), g = f(x * x))
могу да се рачунају вредности у тачки функција које су већ сачуване у променљивој (изрази попут f[0.5])
може да се рачуна извод функције (изрази попут f')
функције и променљиве се исписују на стандардни излаз (наредбе попут f, sin(g(x)), g'[-1])
наредбе се завршавају новим редовима

Дакле, дат је програмски језика за рад са функцијама које можемо да компонујемо, рачунамо њихов извод, као и вредност у тачки, док имамо само два типа наредби—испис и доделу. Пример програма:

f = sin(x)
f'

f[1]
g = 1 + f(x*x)
g
g[0.5]


g'
g'[0.5]

Задатак је да направимо:

интерпретер за овај језик
формирамо синтаксно стабло за њега које може да се исписује и интерпретира

Ово значи да је потребно да направимо два Bison пројекта, где ћемо у првом да вршимо интерпретацију, а у другом да формирамо синтаксно стабло.

Ово је тренутак где можете да покушате да урадите задатак самостално. Главна новина биће рад са непримитивним подацима, у овом случају, функцијама. Због тога је потребно направити одговарајући класни тип података који би их представљао.

Парсер

Као и свим задацима, почињемо од писања граматике језика и прављења парсера за језик који проверава само синтаксичку исправност улаза. Зато је потребно да направимо три фајла:

lexer.l (Flex фајл)
parser.ypp (Bison фајл)
Makefile

Граматика језика

Крећемо од граматике и језика које иницијално попуњавамо празним акцијама. Сегмент акција може да изледа овако:

parser.ypp

program
    : niz_naredbi {}
    ;

niz_naredbi
    : niz_naredbi naredba {}
    | naredba {}
    ;

naredba
    : ID '=' izraz '\n' {}
    | izraz '\n' {}
    | '\n' {}
    ;

izraz
    : izraz '+' izraz {}
    | izraz '-' izraz {}
    | izraz '*' izraz {}
    | izraz '/' izraz {}
    | '-' izraz %prec UMINUS {}
    | '(' izraz ')' {}
    | izraz '\'' {}
    | izraz '[' BROJ ']' {}
    | izraz '(' izraz ')' {}
    | SIN '(' izraz ')' {}
    | COS '(' izraz ')' {}
    | BROJ {}
    | ID {}
    | PROMENLJIVA {}
    ;

Наредбе се не раздвајају ; већ новим редовима (симболом \n). То за последицу има да ћемо у правилима за нетерминал naredba да додамо правило које одговара празној наредби. Ово је потребно у случају да имамо више узастопних празних редова.

У правилима за izraz имамо правило izraz -> PROMENLJIVA које одговара симболу x у дефинисању функција (тј. идентичкој функцији). Потребно је да га разликујемо јер је x у нашем језику резервирана реч.

Осим њега, поменимо да правило izraz -> izraz '(' izraz ')' одговара композицији функција, док су остала правила виђена у грађењу израза.

Када само написали правила граматике, потребно је да декларишемо све терминале (који нису једнокарактерски). Односно, у сегмент дефиниција додајемо:

parser.ypp

%token SIN COS PROMENLJIVA
%token ID
%token BROJ

Међутим, нисмо готови—потребно је да разрешимо вишезначност наше граматике.

Shift/reduce конфликти

Ако бисмо покушали да преведемо овакав Bison фајл, добили бисмо наредну поруку.

parser.ypp: warning: 35 shift/reduce conflicts [-Wconflicts-sr]
parser.ypp: note: rerun with option '-Wcounterexamples' to generate conflict counterexamples

Shift/reduce конфликти најчешће значе да имамо проблема са приоритетом и решаваћемо их тако што дефинишемо асоцијативност и приоритет токена. Од ових 35 конфликата сигурно су неки узроковани приоритетом основних аритметичких операција. Зато додајмо у сегмент дефиниција:

parser.ypp

%left '+' '-'
%left '*' '/'
%right UMINUS

И у правила граматике за унарни минус:

parser.ypp

izraz
    ...
    | '-' izraz %prec UMINUS {}
    ...

Поновним превођењем фајла parser.ypp добијамо нови испис.

parser.ypp: warning: 15 shift/reduce conflicts [-Wconflicts-sr]
parser.ypp: note: rerun with option '-Wcounterexamples' to generate conflict counterexamples

Дакле, нисмо решили све конфликте. У случају када нисмо сигурни где настају конфликти, односно, када не знамо којим токенима треба да доделимо приоритет, можемо да преведемо Bison фајл са опцијом -Wcounterexamples.

Излаз који добијамо при таквом покретању ће бити суштински низ контрапримера, од којих је сваки наредног облика:

parser.ypp: warning: shift/reduce conflict on token '\'' [-Wcounterexamples]
  Example: izraz '+' izraz • '\''
  Shift derivation
    izraz
    ↳ 7: izraz '+' izraz
                   ↳ 13: izraz • '\''
  Reduce derivation
    izraz
    ↳ 13: izraz                  '\''
          ↳ 7: izraz '+' izraz •

Овде ће нам бити најзначајније прве две линије. Прва нам говори на ком токену настаје конфликт, односно, ком то токену треба да доделимо приоритет да бисмо разрешили конфликт. Док друга линија, након Example:, исписује контрапример који нам може помоћи за дубље разумевање проблема.

Наиме, овде видимо да конфликт настаје на токену '\'' тј. треба да доделимо приоритет оператору извода. То заиста потврђује и генерисани пример на другој линији. Парсер не зна како да тумачи реч izraz '+' izraz '\'': да ли као

(izraz '+' izraz) '\'',
или као izraz '+' (izraz '\'')?

Зато треба да дефинишемо приоритет оператора за извод, тј. да додамо у сегмент дефиниција:

parser.ypp

%left '+' '-'
%left '*' '/'
%right UMINUS
%right '\''

Међутим, ово није све јер Bison пријављује још конфликата. Неки од њих су следећи:

parser.ypp: warning: shift/reduce conflict on token '[' [-Wcounterexamples]
  Example: izraz '+' izraz • '[' BROJ ']'

parser.ypp: warning: shift/reduce conflict on token '(' [-Wcounterexamples]
  Example: izraz '+' izraz • '(' izraz ')'

Дакле, имамо проблем код оператора рачунања вредности функције у тачки и оператора композиције. На пример, није јасно како израз izraz '+' izraz '[' BROJ ']' треба да се тумачи. Да ли као:

(izraz '+' izraz) '[' BROJ ']',
или као izraz '+' (izraz '[' BROJ ']')

Слично и код заграда () за композицију.

За разлику од претходних случајева, где је операторима одговарао само један токен (нпр. за сабирање, одузимање, извод и друге), овде оператор одређују два токена—одговарајућа отворена и затворена заграда. Из тог разлога, може бити нејасно како да одредимо приоритет у овом случају тј. ком од та два токена треба доделити приоритет?

Међутим, Bison нам даје одговор на то питање у првим редовима одговарајућих генерисаних контрапримера. Конфликти настају на токенима '[' и '(', и потребно је и довољно само њима доделити приоритет. Дакле, у ситуацијама сличним овим, потребно је доделити приоритет левој загради!

Коначно, треба да додамо у сегменту дефиниција следеће:

parser.ypp

%left '+' '-'
%left '*' '/'
%right UMINUS
%precedence '(' '['
%right '\''

Подсетимо се да су дозвољене декларације асоцијативности:

%left - лева асоцијативност

%right - десна асоцијативност

%nonassoc- неасоцијативан оператор (грешка при извршавању ако се јави потреба за разрешавањем асоцијативности)

%precedence - без навођења асоцијативности

Желимо да заграде буду међусобно истог приоритета, који је већи од приоритета аритметичких операција, али је мањи од извода. Осим тога, не додељујемо им никакву асоцијативност, већ само користимо директиву %precedence да бисмо могли да их наведемо на одговарајућем месту и спецификујемо им приоритет на тај начин (није неопходно користити %precedence овде, може се користити и нпр. %left али је дато ради комплетности).

Објашњење зашто је довољно доделити приоритете левим заградама, као и шта су заправо shift/reduce конфликти, се може наћи у додатку. Оно може бити од користи за разрешавање конфликата у случајевима који нису покривени овде, али и за дубље разумевање рада парсера у позадини.

Лексер

Сада је могуће написати и лексер јер знамо који су нам токени потребни.

lexer.l

%option noyywrap

%{
    #include <iostream>
    #include <cstdlib>
    #include "parser.tab.hpp"
%}

PRIR_BROJ 0|[1-9][0-9]*
REAL_BROJ [+-]?{PRIR_BROJ}(\.{PRIR_BROJ}([eE][+-]{PRIR_BROJ})?)?
IDENTIFIKATOR [_a-zA-Z][_a-zA-Z0-9]*

%%

x {
    return PROMENLJIVA;
}

sin {
    return SIN;
}

cos {
    return COS;
}

{IDENTIFIKATOR} {
    return ID;
}

{REAL_BROJ} {
    return BROJ;
}

[+\-*/()\[\]='\n] {
    return *yytext;
}

[ \t] {

}

. {
    std::cerr << "leksicka greska: " << yytext << std::endl;
    exit(EXIT_FAILURE);
}

%%

Приметимо да сада симбол за нови ред \n не игноришемо јер нам је он сепаратор наредби.

Повезивање

Направимо још и Make фајл зарад лакшег превођења. Он може да изледа овако:

Makefile

CC = g++
CFLAGS = -Wall -Wextra

parser: lex.yy.o parser.tab.o
	$(CC) $(CFLAGS) $^ -o $@

lex.yy.o: lex.yy.c
	$(CC) $(CFLAGS) -c $< -o $@

lex.yy.c: lexer.l parser.tab.hpp
	flex --nounput $<

parser.tab.o: parser.tab.cpp parser.tab.hpp
	$(CC) $(CFLAGS) -c $< -o $@

parser.tab.cpp parser.tab.hpp: parser.ypp
	bison --header $<

.PHONY: clean
clean:
	rm -f *.o parser lex.yy.c parser.tab.*

Превођењем и покретањем добијамо парсер за наш језик. Оно што је важно је да ћемо у оба наредна дела тј. и за интерпретер, и за синтаксно стабло, да користимо исту граматику. Дакле, само ће се разликовати акције у правилима граматике.

Интерпретација

Први део задатка је да направимо интерпретер за овај језик. То значи да треба да попунимо постојећа правила граматике одговарајућим акцијама које би извршавале наредбе програма.

Приметимо да наш програм треба да ради са функцијама—може да их чува, извршава основне аритметичке операције над њима, исписује их, компонује, рачуна извод и вредност у тачки. Дакле, радимо са сложеним типом података и пожељно је да направимо посебну класу која би представљала тај тип, док би сву логику ставили у одговарајуће методе те класе.

Зато правимо нову класу Funkcija и два нова фајла funkcija.hpp и funkcija.cpp у којима ћемо да имплементирамо ову класу.

Међутим, једна класа нам не може бити довољна да обухватимо целокупну логику функција које нам се појављују. Наиме, посматрајмо наредни програм:

f = sin(x)
f'

g = cos(x)
g'

h = f + g(f(x))
h'

Овде је функција f синусна функција, g косинусна, док је h добијена њиховим комбиновањем. Уколико бисмо имали само једну класу чијег типа би биле све ове функције, поставља се неколико питања. Како ћемо чувати функцију h која није елементарна функција? Како да рачунамо изводе свих поменутих функција које су очигледно доста другачије?

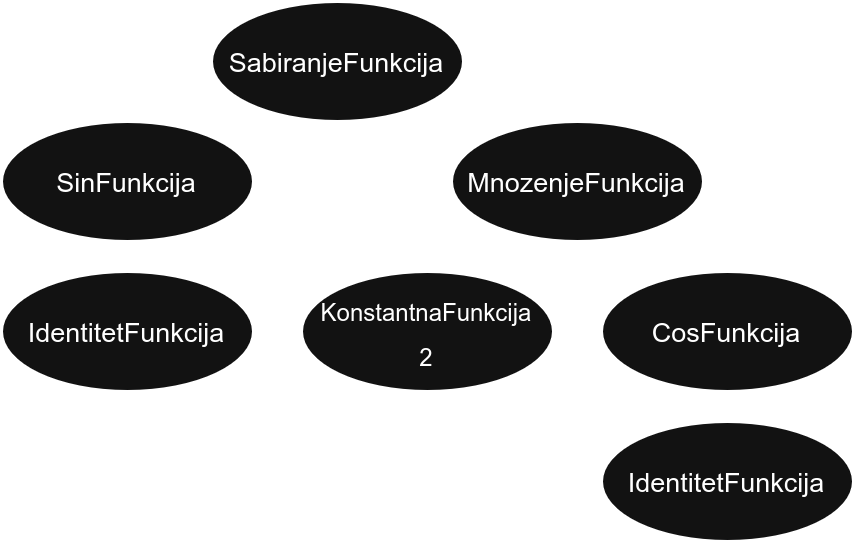
Решење које ћемо овде применити је да функције представљамо дрволиком структуром чији ће чворови бити елементарне функције (константна, идентичка, sin, cos, негација, сабирање, одузимање, множење и дељење) за које ћемо правити засебне класе.

На пример, функција f која је једнака sin(x) ће бити:

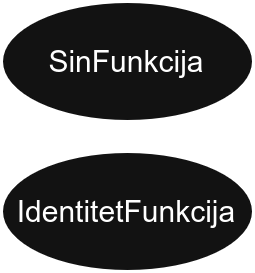
funkcije_sin

Слично, функција g = cos(x) ће бити:

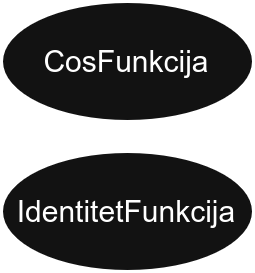
funkcije_cos

Док ће функција h која је једнака sin(x) + cos(sin(x)), бити чувана на следећи начин:

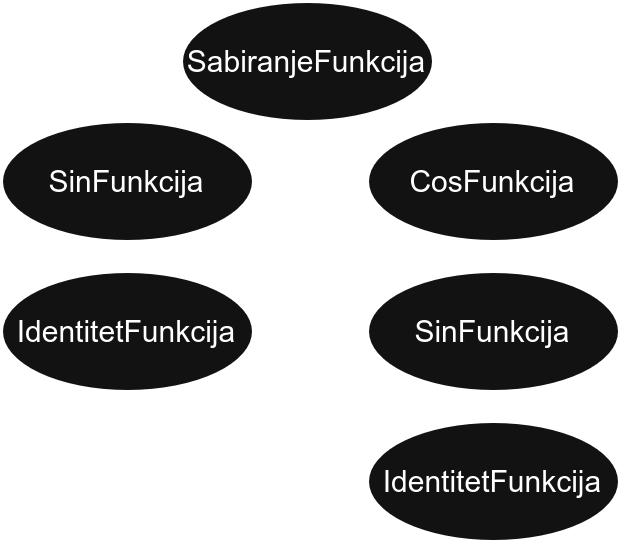
funkcije_kombinacija

Сваки чвор представља неку елементарну функцију, док деца представљају аргументе те функције. Зато неки чворови имају два детета (попут SabiranjeFunkcija), неки једно (попут SinFunkcija), а неки ниједно (као што је IdentitetFunkcija).

Да бисмо ово имплементирали, биће нам потребна апстрактна класа коју ће све функције наслеђивати, и то ће бити класа Funkcija. Остале класе ће поштовати следећу хијерархију:

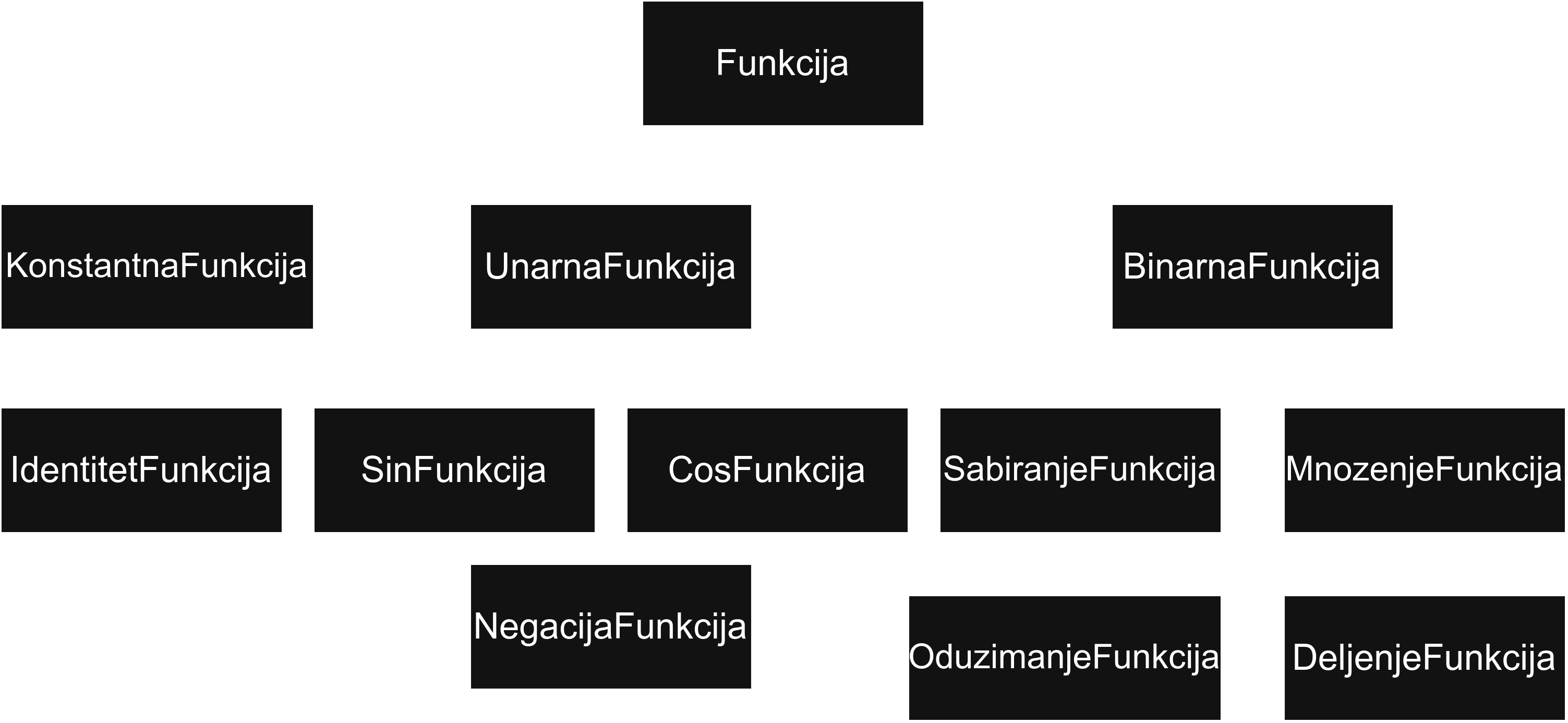
funkcije_hijerarhija

Приметимо да уводимо помоћне апрстрактне класе UnarnaFunkcija и BinarnaFunkcija које ће наслеђивати све функције са једним, односно два детета. На тај начин олакшавамо мало посао око писања свих класа, јер ће се сва заједничка логика за нпр. класе које представљају унарне функције налазити у тој апстрактној међукласи, чиме смањујемо дупликацију кода.

Напомена: Приметимо да ова хијерархија доста подсећа на хијерархију коју смо користили код синтаксних стабала. Међутим, ове класе нису класе које ћемо користити за чворове синтаксног стабла! Касније ће бити детаљније објашњење о разлици, али за сада треба да посматрамо да овде правимо само интерпретер који је потпуно независан од другог дела задатка (формирања синтаксног стабла). Из тог разлога имена свих класа имају суфикс Funkcija.

Ипак, пожељно је упознати се са хијерархијом синтаксног стабла из претходних лекција, и даље ће бити ће се користити имплементационе технике и идеје које су тамо покривене.

Класа `Funkcija`

Класа Funkcija је на врху хијерархије и представља апстрактну класу које ће све остале наслеђивати. Она треба да декларише и све методе које једна функција у нашем програму треба да имплементира. То су методе за испис функције, рачунање вредности функције у тачки, за извод и за композицију са другом функцијом.

Поред њих, како је ово апстрактна класа коју ће наслеђивати класе које чувају показиваче (правимо дрволику структуру), то ће бити потребно да декларишемо и виртуелни дестуктор у овој класи, али и методу kloniraj која ће служити за прављење копије функције.

Декларација може да изгледа овако:

funkcija.hpp

class Funkcija {
public:
    virtual ~Funkcija();
    virtual double izracunaj(double vrednost) const = 0;
    virtual void ispisi(std::ostream &os) const = 0;
    virtual Funkcija *izvod() const = 0;
    virtual Funkcija *komponuj(Funkcija *funkcija) const = 0;
    virtual Funkcija *kloniraj() const = 0;
};

std::ostream &operator<<(std::ostream &os, const Funkcija &funkcija);

Метода izracunaj прима реалан број и враћа реалан број који представља вредност функције у тој тачки.

Метода ispisi исписује функцију на std::ostream што користимо за преоптерећивање оператора <<.

Методе izvod и komponuj су замишљене да не мењају објекат функције над којим се позивају већ да направе нов објекат тј. нову функцију која је једнака изводу, односно нову функцију која одговара композицији, те зато враћају Funkcija * и обележене су кључном речи const.

Што се тиче funkcija.cpp фајла, ту је потребно само дефинисати деструктор (макар он био и празан, јер свака наткласа мора имати деструктор) и преоптеретити оператор <<.

funkcija.cpp

Funkcija::~Funkcija() {}

std::ostream &operator<<(std::ostream &os, const Funkcija &funkcija) {
    funkcija.ispisi(os);
    return os;
}

Класа `KonstantnaFunkcija`

Ова функција треба да чува један реалан број и зато, поред метода које наслеђује, треба још да имплементира одговарајући конструктор. Како чува само један податак који је примитивног типа, не треба да предефинише деструктор.

funkcija.hpp

class KonstantnaFunkcija : public Funkcija {
public:
    KonstantnaFunkcija(double vrednost);

    // metode iz natklase
    double izracunaj(double vrednost) const override;
    void ispisi(std::ostream &os) const override;
    Funkcija *izvod() const override;
    Funkcija *komponuj(Funkcija *funkcija) const override;
    Funkcija *kloniraj() const override;

private:
    double m_vrednost;
};

Одговарајуће имплементације могу да буду попут наредних:

funkcija.cpp

KonstantnaFunkcija::KonstantnaFunkcija(double vrednost)
    : m_vrednost(vrednost) {}


double KonstantnaFunkcija::izracunaj(double vrednost) const {
    return m_vrednost;
}

void KonstantnaFunkcija::ispisi(std::ostream &os) const {
    os << m_vrednost;
}

Funkcija *KonstantnaFunkcija::izvod() const {
    return new KonstantnaFunkcija(0);
}

Funkcija *KonstantnaFunkcija::komponuj(Funkcija *funkcija) const {
    return new KonstantnaFunkcija(*this);
}

Funkcija *KonstantnaFunkcija::kloniraj() const {
    return new KonstantnaFunkcija(*this);
}

Као што смо и напоменули, методе izvod и komponuj не мењају објекат над којим се позивају, већ креирају нови. Из тог разлога метода за извод враћа нову константну функцију која представља нулу, а композиција константне функције са било којом функцијом враћа баш ту константну функцију.

У овим методама позивамо подразумевани конструктор копије који нам је овде довољан јер класа чува само примитиван тип.

Класа `IdentitetFunkcija`

Ова класа представља идентичку функцију (коју у програму означавамо са x). Она не треба да чува никакав додатни податак, већ само да имплементира методе наткласе.

funkcija.hpp

class IdentitetFunkcija : public Funkcija {
public:
    // metode iz natklase
    double izracunaj(double vrednost) const override;
    void ispisi(std::ostream &os) const override;
    Funkcija *izvod() const override;
    Funkcija *komponuj(Funkcija *funkcija) const override;
    Funkcija *kloniraj() const override;
};

funkcija.cpp

double IdentitetFunkcija::izracunaj(double vrednost) const {
    return vrednost;
}

void IdentitetFunkcija::ispisi(std::ostream &os) const {
    os << "x";
}

Funkcija *IdentitetFunkcija::izvod() const {
    return new KonstantnaFunkcija(1);
}

Funkcija *IdentitetFunkcija::komponuj(Funkcija *funkcija) const {
    return funkcija->kloniraj(); // moramo da pravimo kopiju!
}

Funkcija *IdentitetFunkcija::kloniraj() const {
    return new IdentitetFunkcija(*this);
}

Овде је важно обратити пажњу да метода komponuj не може само да прослеђује аргумент funkcija. Тј. не може само да буде

Funkcija *IdentitetFunkcija::komponuj(Funkcija *funkcija) const {
    return funkcija;
}

већ је неопходно да прави копију аргумента. Разлог за то је што метода komponuj ради тако што рекурзивно обилази функцију и на листове надовезује функцију аргумент. Зато, уколико постоји више листова, желимо сваки пут да правимо нову копију функције.

Погледајмо на примеру. Нека је дата функција f = sin(x) + 2 * cos(x).

funkcije_komponuj_osnova

И желимо да је компонујемо са функцијом g = cos(x).

funkcije_cos

Њихова композиција f(g(x)) = sin(cos(x)) + 2 * cos(cos(x)) ће бити нова функција која изгледа овако:

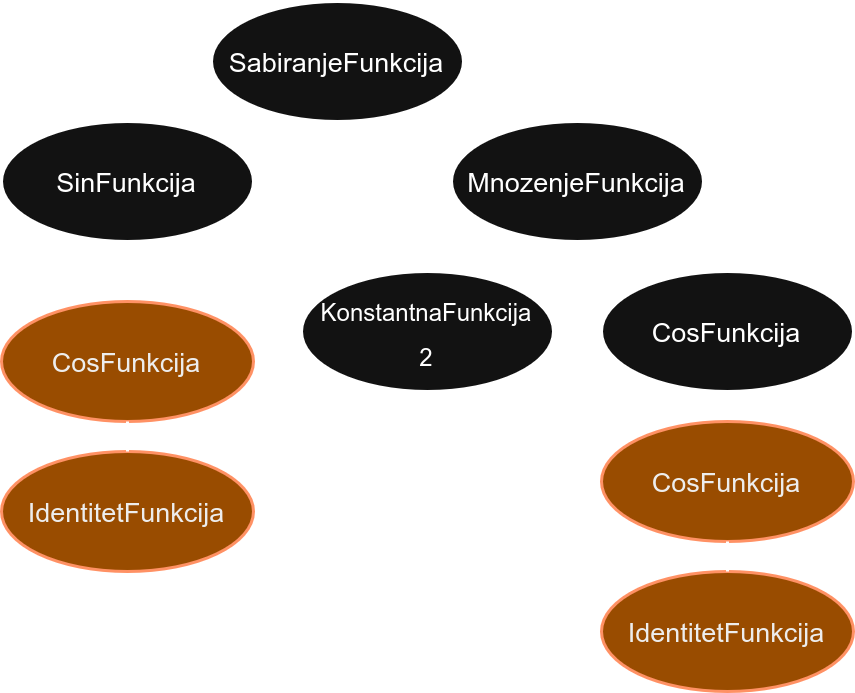
funkcije_komponuj_kompozicija

Позив методе f->komponuj(g) ће покренути позив методе komponuj над свим чворовима стабла функције f и прослеђиваће се све до листова где ће се (у зависноти од типа листа) надовезати функција g.

У овом примеру, листови функције f су два чвора типа IdentitetFunkcija и један KonstantnaFunkcija. Као што смо видели, константна функција не треба ништа да промени, док идентична функција треба да постави функцију g уместо себе.

Уколико бисмо у методи IdentitetFunkcija::komponuj само враћали аргумент, добили бисмо следеће стабло:

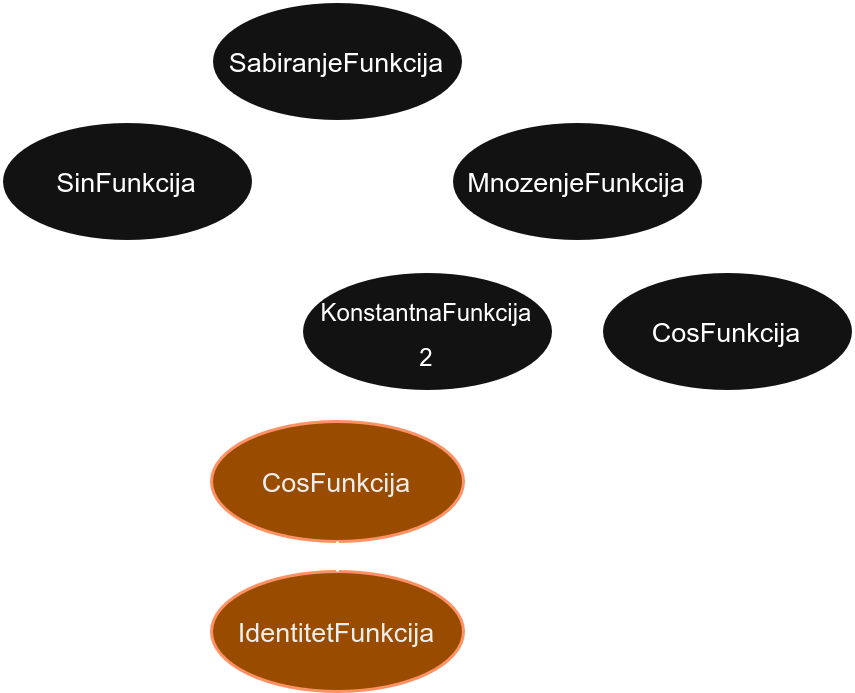
funkcije_komponuj_kompozicija_lose

Дакле, не бисмо правили посебне копије за сваки лист, већ бисмо само превезали показиваче. То није жељено понашање у овом случају (нпр. направиће проблем приликом позива деструктора), те је неопходно да правимо копију у имплементацији методе тј. треба да стоји

Funkcija *IdentitetFunkcija::komponuj(Funkcija *funkcija) const {
    return funkcija->kloniraj();
}

Класа `UnarnaFunkcija`

Ово је међукласа која обједињује заједничке делове свих класа које представљају функције са једним аргументом. Биће готово идентична класи UnarniCvor из лекције о синтаксним стаблима.

Чуваће један показивач на функцију који представља аргумент. Чим чувамо показиваче на динамички алоцирану меморију, потребно је да предефинишемо деструктор и конструктор копије (слично као раније, ни овде нећемо да предефинишемо оператор доделе).

funkcija.hpp

class UnarnaFunkcija : public Funkcija {
public:
    UnarnaFunkcija(Funkcija *funkcija);
    UnarnaFunkcija(const UnarnaFunkcija &druga);
    ~UnarnaFunkcija();

    // metode iz natklase
    virtual double izracunaj(double vrednost) const = 0;
    virtual void ispisi(std::ostream &os) const = 0;
    virtual Funkcija *izvod() const = 0;
    virtual Funkcija *komponuj(Funkcija *funkcija) const = 0;
    virtual Funkcija *kloniraj() const = 0;

protected:
    Funkcija *m_funkcija;
};

funkcija.cpp

UnarnaFunkcija::UnarnaFunkcija(Funkcija *funkcija)
    : m_funkcija(funkcija) {}

UnarnaFunkcija::UnarnaFunkcija(const UnarnaFunkcija &druga) {
    m_funkcija = druga.m_funkcija->kloniraj();
}

UnarnaFunkcija::~UnarnaFunkcija() {
    delete m_funkcija;
}

У наставку су дате класе које је наслеђују: NegacijaFunkcija, SinFunkcija и CosFunkcija.

Ниједна од њих неће имати нова поља, али ће бити неопходно да свака дефинише конструктор истог потписа као конструктор из наткласе UnarnaFunkcija. Поред тога, неће бити потребно предефинисати ни деструктор, ни конструктор копије јер ће се наследити одговарајући из наткласе.

Класа `NegacijaFunkcija`

funkcija.hpp

class NegacijaFunkcija : public UnarnaFunkcija {
public:
    NegacijaFunkcija(Funkcija *funkcija);

    // metode iz natklase
    double izracunaj(double vrednost) const override;
    void ispisi(std::ostream &os) const override;
    Funkcija *izvod() const override;
    Funkcija *komponuj(Funkcija *funkcija) const override;
    Funkcija *kloniraj() const override;
};

funkcija.cpp

NegacijaFunkcija::NegacijaFunkcija(Funkcija *funkcija)
    : UnarnaFunkcija(funkcija) {}

double NegacijaFunkcija::izracunaj(double vrednost) const {
    return - m_funkcija->izracunaj(vrednost);
}

void NegacijaFunkcija::ispisi(std::ostream &os) const {
    os << "- (" << *m_funkcija << ")";
}

Funkcija *NegacijaFunkcija::izvod() const {
    return new NegacijaFunkcija(m_funkcija->izvod());
}

Funkcija *NegacijaFunkcija::komponuj(Funkcija *funkcija) const {
    return new NegacijaFunkcija(m_funkcija->komponuj(funkcija));
}

Funkcija *NegacijaFunkcija::kloniraj() const {
    return new NegacijaFunkcija(*this);
}

Приметимо како се у методи komponuj прво врши композиција подфункције, а онда се прави нова функција. То се уклапа уз поменути опис да се композиција извршава тако што обилазимо функцију до листова, а затим у повратку формирамо нову коју враћамо као резултат.

Класа `SinFunkcija`

funkcija.hpp

class SinFunkcija : public UnarnaFunkcija {
public:
    SinFunkcija(Funkcija *funkcija);

    // metode iz natklase
    double izracunaj(double vrednost) const override;
    void ispisi(std::ostream &os) const override;
    Funkcija *izvod() const override;
    Funkcija *komponuj(Funkcija *funkcija) const override;
    Funkcija *kloniraj() const override;
};

funkcija.cpp

SinFunkcija::SinFunkcija(Funkcija *funkcija)
    : UnarnaFunkcija(funkcija) {}

double SinFunkcija::izracunaj(double vrednost) const {
    return sin(m_funkcija->izracunaj(vrednost));
}

void SinFunkcija::ispisi(std::ostream &os) const {
    os << "sin(" << *m_funkcija << ")";
}

Funkcija *SinFunkcija::izvod() const {
    return new MnozenjeFunkcija(
        new CosFunkcija(m_funkcija->kloniraj()),
        m_funkcija->izvod()
    );
}

Funkcija *SinFunkcija::komponuj(Funkcija *funkcija) const {
    return new SinFunkcija(m_funkcija->komponuj(funkcija));
}

Funkcija *SinFunkcija::kloniraj() const {
    return new SinFunkcija(*this);
}

Овде треба обратити пажњу на методу izvod. Наиме, важи следеће

(sin(m_funkcija))' = cos(m_funkcija) * m_funkcija'

Што је и записано у имплементацији ове методе. Међутим, приметимо да правимо копију функције m_funkcija. Разлог за то је што метода за извод треба да врати потпуно нови објекат, па желимо да копирамо све постојеће објекте, а не само да превежемо показиваче ка њима (сличан разлог као код методе komponuj у IdentitetFunkcija).

Класа `CosFunkcija`

funkcija.hpp

class CosFunkcija : public UnarnaFunkcija {
public:
    CosFunkcija(Funkcija *funkcija);

    // metode iz natklase
    double izracunaj(double vrednost) const override;
    void ispisi(std::ostream &os) const override;
    Funkcija *izvod() const override;
    Funkcija *komponuj(Funkcija *funkcija) const override;
    Funkcija *kloniraj() const override;
};

funkcija.cpp

CosFunkcija::CosFunkcija(Funkcija *funkcija)
    : UnarnaFunkcija(funkcija) {}

double CosFunkcija::izracunaj(double vrednost) const {
    return cos(m_funkcija->izracunaj(vrednost));
}

void CosFunkcija::ispisi(std::ostream &os) const {
    os << "cos(" << *m_funkcija << ")";
}

Funkcija *CosFunkcija::izvod() const {
    return new NegacijaFunkcija(
        new MnozenjeFunkcija(
            new SinFunkcija(m_funkcija->kloniraj()),
            m_funkcija->izvod()
        )
    );
}

Funkcija *CosFunkcija::komponuj(Funkcija *funkcija) const {
    return new CosFunkcija(m_funkcija->komponuj(funkcija));
}

Funkcija *CosFunkcija::kloniraj() const {
    return new CosFunkcija(*this);
}

Аналогно синусног функцији, овде за извод имамо наредно правило:

(cos(m_funkcija))' = - sin(m_funkcija) * m_funkcija'

Класа `BinarnaFunkcija`

Ово је апстрактна класа која треба да представља функције са два аргумента. Њена структура је слична структури класе UnarnaFunkcija са главном разликом да ће чувати два показивача уместо једног.

Због чувања показивача, потребно је да предефинишемо подразумевани деструктор и конструктор копије.

funkcija.hpp

class BinarnaFunkcija : public Funkcija {
public:
    BinarnaFunkcija(Funkcija *leva, Funkcija *desna);
    BinarnaFunkcija(const BinarnaFunkcija &druga);
    ~BinarnaFunkcija();

    // metode iz natklase
    virtual double izracunaj(double vrednost) const = 0;
    virtual void ispisi(std::ostream &os) const = 0;
    virtual Funkcija *izvod() const = 0;
    virtual Funkcija *komponuj(Funkcija *funkcija) const = 0;
    virtual Funkcija *kloniraj() const = 0;

protected:
    Funkcija *m_leva, *m_desna;
};

funkcija.cpp

BinarnaFunkcija::BinarnaFunkcija(Funkcija *leva, Funkcija *desna)
    : m_leva(leva), m_desna(desna) {}

BinarnaFunkcija::BinarnaFunkcija(const BinarnaFunkcija &druga) {
    m_leva = druga.m_leva->kloniraj();
    m_desna = druga.m_desna->kloniraj();
}

BinarnaFunkcija::~BinarnaFunkcija() {
    delete m_leva;
    delete m_desna;
}

Дакле, ово је апстрактна класа и све преостале методе треба да дефинишу класе које је наслеђују. У овом случају, то су класе SabiranjeFunkcija, OduzimanjeFunkcija, MnozenjeFunkcija и DeljenjeFunkcija.

Опет, зато што смо предефинисали деструктор и конструктор копије у наткласи, за ове класе биће довољно само да дефинишемо одговарајући конструктор. Имплементације су у наставку.

Класа `SabiranjeFunkcija`

funkcija.hpp

class SabiranjeFunkcija : public BinarnaFunkcija {
public:
    SabiranjeFunkcija(Funkcija *leva, Funkcija *desna);

    // metode iz natklase
    double izracunaj(double vrednost) const override;
    void ispisi(std::ostream &os) const override;
    Funkcija *izvod() const override;
    Funkcija *komponuj(Funkcija *funkcija) const override;
    Funkcija *kloniraj() const override;
};

funkcija.cpp

SabiranjeFunkcija::SabiranjeFunkcija(Funkcija *leva, Funkcija *desna)
    : BinarnaFunkcija(leva, desna) {}

double SabiranjeFunkcija::izracunaj(double vrednost) const {
    return m_leva->izracunaj(vrednost) + m_desna->izracunaj(vrednost);
}

void SabiranjeFunkcija::ispisi(std::ostream &os) const {
    os << "(" << *m_leva << ") + (" << *m_desna << ")";
}

Funkcija *SabiranjeFunkcija::izvod() const {
    return new SabiranjeFunkcija(
        m_leva->izvod(),
        m_desna->izvod()
    );
}

Funkcija *SabiranjeFunkcija::komponuj(Funkcija *funkcija) const {
    return new SabiranjeFunkcija(
        m_leva->komponuj(funkcija),
        m_desna->komponuj(funkcija)
    );
}

Funkcija *SabiranjeFunkcija::kloniraj() const {
    return new SabiranjeFunkcija(*this);
}

Класа `OduzimanjeFunkcija`

funkcija.hpp

class OduzimanjeFunkcija : public BinarnaFunkcija {
public:
    OduzimanjeFunkcija(Funkcija *leva, Funkcija *desna);

    // metode iz natklase
    double izracunaj(double vrednost) const override;
    void ispisi(std::ostream &os) const override;
    Funkcija *izvod() const override;
    Funkcija *komponuj(Funkcija *funkcija) const override;
    Funkcija *kloniraj() const override;
};

funkcija.cpp

OduzimanjeFunkcija::OduzimanjeFunkcija(Funkcija *leva, Funkcija *desna)
    : BinarnaFunkcija(leva, desna) {}

double OduzimanjeFunkcija::izracunaj(double vrednost) const {
    return m_leva->izracunaj(vrednost) - m_desna->izracunaj(vrednost);
}

void OduzimanjeFunkcija::ispisi(std::ostream &os) const {
    os << "(" << *m_leva << ") - (" << *m_desna << ")";
}

Funkcija *OduzimanjeFunkcija::izvod() const {
    return new OduzimanjeFunkcija(
        m_leva->izvod(),
        m_desna->izvod()
    );
}

Funkcija *OduzimanjeFunkcija::komponuj(Funkcija *funkcija) const {
    return new OduzimanjeFunkcija(
        m_leva->komponuj(funkcija),
        m_desna->komponuj(funkcija)
    );
}

Funkcija *OduzimanjeFunkcija::kloniraj() const {
    return new OduzimanjeFunkcija(*this);
}

Класа `MnozenjeFunkcija`

funkcija.hpp

class MnozenjeFunkcija : public BinarnaFunkcija {
public:
    MnozenjeFunkcija(Funkcija *leva, Funkcija *desna);

    // metode iz natklase
    double izracunaj(double vrednost) const override;
    void ispisi(std::ostream &os) const override;
    Funkcija *izvod() const override;
    Funkcija *komponuj(Funkcija *funkcija) const override;
    Funkcija *kloniraj() const override;
};

funkcija.cpp

MnozenjeFunkcija::MnozenjeFunkcija(Funkcija *leva, Funkcija *desna)
    : BinarnaFunkcija(leva, desna) {}

double MnozenjeFunkcija::izracunaj(double vrednost) const {
    return m_leva->izracunaj(vrednost) * m_desna->izracunaj(vrednost);
}

void MnozenjeFunkcija::ispisi(std::ostream &os) const {
    os << "(" << *m_leva << ") * (" << *m_desna << ")";
}

Funkcija *MnozenjeFunkcija::izvod() const {
    return new SabiranjeFunkcija(
        new MnozenjeFunkcija(
            m_leva->izvod(),
            m_desna->kloniraj()
        ),
        new MnozenjeFunkcija(
            m_leva->kloniraj(),
            m_desna->izvod()
        )
    );
}

Funkcija *MnozenjeFunkcija::komponuj(Funkcija *funkcija) const {
    return new MnozenjeFunkcija(
        m_leva->komponuj(funkcija),
        m_desna->komponuj(funkcija)
    );
}

Funkcija *MnozenjeFunkcija::kloniraj() const {
    return new MnozenjeFunkcija(*this);
}

Овде је једина новина рачунање извода. Наиме, важи

(f * g)' = f' * g + f * g'

при чему је важно да водимо рачуна (као и у претходним сличним ситуацијама) да правимо копије одговарајућих објеката.

Класа `DeljenjeFunkcija`

Овде за извод користимо једнакост

(f / g)' = (f' * g - f * g') / (g * g)

funkcija.hpp

class DeljenjeFunkcija : public BinarnaFunkcija {
public:
    DeljenjeFunkcija(Funkcija *leva, Funkcija *desna);

    // metode iz natklase
    double izracunaj(double vrednost) const override;
    void ispisi(std::ostream &os) const override;
    Funkcija *izvod() const override;
    Funkcija *komponuj(Funkcija *funkcija) const override;
    Funkcija *kloniraj() const override;
};

funkcija.cpp

DeljenjeFunkcija::DeljenjeFunkcija(Funkcija *leva, Funkcija *desna)
    : BinarnaFunkcija(leva, desna) {}

double DeljenjeFunkcija::izracunaj(double vrednost) const {
    return m_leva->izracunaj(vrednost) / m_desna->izracunaj(vrednost);
}

void DeljenjeFunkcija::ispisi(std::ostream &os) const {
    os << "(" << *m_leva << ") / (" << *m_desna << ")";
}

Funkcija *DeljenjeFunkcija::izvod() const {
    return new DeljenjeFunkcija(
        new OduzimanjeFunkcija(
            new MnozenjeFunkcija(
                m_leva->izvod(),
                m_desna->kloniraj()
            ),
            new MnozenjeFunkcija(
                m_leva->kloniraj(),
                m_desna->izvod()
            )
        ),
        new MnozenjeFunkcija(
            m_desna->kloniraj(),
            m_desna->kloniraj()
        )
    );
}

Funkcija *DeljenjeFunkcija::komponuj(Funkcija *funkcija) const {
    return new DeljenjeFunkcija(
        m_leva->komponuj(funkcija),
        m_desna->komponuj(funkcija)
    );
}

Funkcija *DeljenjeFunkcija::kloniraj() const {
    return new DeljenjeFunkcija(*this);
}

Акције у Bison-у

Да бисмо коначно извршили интерпретацију нашег програма, потребно је да попунимо акције граматике у Bison фајлу.

Како у нашем програмском језику дозвољавамо употребу променљивих, за извршавање ће бити потребно да обезбедимо механизам чувања променљивих и њихових вредности. То смо до сада радили тако што смо чували једну глобалну мапу типа std::map<std::string, tip_izraza> где је tip_izraza тип променљивих са којим радимо у програму (нпр. double ако су променљиве реални бројеви). То ћемо и овде урадити, али ћемо, налик претходним лекцијама, направити посебну омотач-класу око мапе таквог типа и сву логику ћемо енкапсулирати унутар ње. Зато правимо класу TabelaSimbola за те потребе.

Поред тога, класа TabelaSimbola ће нам бити потребна за други део задатка—формирање синтаксног стабла.

Класа `TabelaSimbola`

Ова класа је суштински иста као и она из лекције о синтаксним стаблима, међутим, постоји једна битна разлика. Овде су нам изрази сложеног типа Funkcija и променљиве треба да чувају вредности тог типа. Када је потребно да чувамо променљиве сложеног типа увек ћемо чувати показиваче на њих. У овом случају, то ће значити да ће мапа бити типа:

std::map<std::string, Funkcija *>

Поново, када год видимо показиваче (који показују на динамички алоцирану меморију), треба да размишљамо о њиховом ослобађању. Зато ће нам овде бити потребно да предефинишемо деструктор (конструктор копије и оператор доделе нам неће бити потребни).

tabela_simbola.hpp

#ifndef TABELA_SIMBOLA_HPP
#define TABELA_SIMBOLA_HPP

#include <map>
#include "funkcija.hpp"

class TabelaSimbola {
public:
    ~TabelaSimbola();

    void dodeli_vrednost(const std::string &promenljiva, Funkcija *vrednost);
    Funkcija *vrednost_promenljive(const std::string &promenljiva) const;

private:
    std::map<std::string, Funkcija *> m_tabela;
};

#endif

tabela_simbola.cpp

#include "tabela_simbola.hpp"

TabelaSimbola::~TabelaSimbola() {
    for (auto &p : m_tabela) {
        delete p.second;
    }
}

void TabelaSimbola::dodeli_vrednost(const std::string &promenljiva, Funkcija *vrednost) {
    auto it = m_tabela.find(promenljiva);
    if (it != m_tabela.end()) {
        delete it->second;
    }
    m_tabela[promenljiva] = vrednost;
}

Funkcija *TabelaSimbola::vrednost_promenljive(const std::string &promenjliva) const {
    auto it = m_tabela.find(promenjliva);
    if (it == m_tabela.end()) {
        std::cerr << "promenljiva " << promenjliva << " nije definisana" << std::endl;
        exit(EXIT_FAILURE);
    }
    return it->second;
}

Још једном напоменимо да у имплементацији методе vrednost_promenljive не можемо да урадимо само:

return m_tabela[promenljiva]; // greska!

јер она константна метода, већ морамо да користимо методу find.

Већ сада можемо да дефинишемо једну глобалну променљиву овог типа у parser.ypp фајлу коју ћемо користити у акцијама за рад са променљивама. Зато додајемо у сегменту дефиниција, у делу за C++ код следеће:

parser.ypp

%{
    #include "tabela_simbola.hpp"

    // ...

    TabelaSimbola tabela_simbola;
%}

Акције

Сада можемо да попуњавамо правила граматике одговарајућим акцијама. Главни део биће како интерпретирати правила за нетерминал izraz тј. како формирати изразе током парсирања. То радимо слично као и до сада (није лоше подсетити се како се извршавају акције у позадини).

Акције за основне аритметичке операције функција су следеће:

parser.ypp

izraz
    : izraz '+' izraz {
        $$ = new SabiranjeFunkcija($1, $3);
    }
    | izraz '-' izraz {
        $$ = new OduzimanjeFunkcija($1, $3);
    }
    | izraz '*' izraz {
        $$ = new MnozenjeFunkcija($1, $3);
    }
    | izraz '/' izraz {
        $$ = new DeljenjeFunkcija($1, $3);
    }
    | '-' izraz %prec UMINUS {
        $$ = new NegacijaFunkcija($2);
    }
    | '(' izraz ')' {
        $$ = $2;
    }
    | BROJ {
        $$ = new KonstantnaFunkcija($1);
    }

Дакле, приликом парсирања израза само креирамо одговарајуће функције. Ово значи да желимо да нам нетерминал izraz буде типа Funkcija * и то морамо да наведемо парсеру. Поред тога, биће потребно да наведемо да је токен BROJ типа double, и токен ID показивач на ниску. Зато додајемо у сегмент дефиниција:

parser.ypp

%union {
    double realan_broj;
    std::string *niska;
    Funkcija *funkcija;
}

%token SIN COS PROMENLJIVA
%token<niska> ID
%token<realan_broj> BROJ

%type<funkcija> izraz

Не заборавимо да додамо лексеру одговарајуће акције приликом препознавања бројева, односно идентификатора. Прецизније, треба да сачува вредности у одговарајуће поље променљиве yylval.

lexer.l

{IDENTIFIKATOR} {
    yylval.niska = new std::string(yytext);
    return ID;
}

{REAL_BROJ} {
    yylval.realan_broj = atof(yytext);
    return BROJ;
}

Сада можемо да наставимо са попуњавањем преосталих правила за изразе.

parser.ypp

izraz
    : ID {
        $$ = tabela_simbola.vrednost_promenljive(*$1)->kloniraj();
        delete $1;
    }

Дакле, када се приликом парсирања наиђе на идентификатор, оно што интерпретер треба да уради је да врати вредности променљиве коју тај идентификатор представља. Зато користимо претходно дефинисану променљиву tabela_simbola и над њом позивамо методу која враћа вредност променљиве. Међутим, овде је важно да враћени објекат копирамо (тј. позовемо методу kloniraj) јер не радимо са примитивним типовима, већ табела симбола чува показиваче на наш дефинисани тип. У супротном, при сваком парсирању конкретног идентификатора бисмо враћали увек исти објекат, што није семантика коју желимо (такво притко копирање ће нпр. изазвати проблем вишеструког ослобађања меморије).

Остају наредне акције за попунавање:

parser.ypp

izraz
    : izraz '\'' {
        $$ = $1->izvod();
        delete $1;
    }
    | izraz '[' BROJ ']' {
        $$ = new KonstantnaFunkcija($1->izracunaj($3));
        delete $1;
    }
    | izraz '(' izraz ')' {
        $$ = $1->komponuj($3);
        delete $1;
        delete $3;
    }
    | SIN '(' izraz ')' {
        $$ = new SinFunkcija($3);
    }
    | COS '(' izraz ')' {
        $$ = new CosFunkcija($3);
    }
    | PROMENLJIVA {
        $$ = new IdentitetFunkcija();
    }

Ове акције представљају једноставне позиве одговарајућих метода које смо већ имплементирали. Међутим, њихова тежина се огледа у правилном управљању меморијом, за које је потребно да разумемо шта нам тачно раде методе које позивамо.

На пример, погледајмо акцију за извод.

parser.ypp

izraz
    : izraz '\'' {
        $$ = $1->izvod();
        delete $1;
    }

Приликом дизајна класе Funkcija смо изабрали да метода izvod креира нови објекат типа Funkcija и враћа показивач на њега. То значи да ће након прве доделе у акцији, показивач $1 показивати на меморију која нам више није потребна, те је одмах ослобађамо. Слично и у осталим правилима водимо рачуна шта нам више није потребно и позивамо деструкторе над тим објектима.

Када смо формирали изразе, остају још наредбе.

parser.ypp

naredba
    : ID '=' izraz '\n' {
        tabela_simbola.dodeli_vrednost(*$1, $3);
        delete $1;
    }
    | izraz '\n' {
        std::cout << *$1 << std::endl;
        delete $1;
    }
    | '\n' {}
    ;

Чиме комплетирамо наш парсер. Сада остаје још да га преведемо и тестирамо. За то је потребно да у Makefile додамо правила за превођење класа за функције као и за табелу симбола.

Makefile

CC = g++
CFLAGS = -Wall -Wextra

parser: lex.yy.o parser.tab.o funkcija.o tabela_simbola.o
	$(CC) $(CFLAGS) $^ -o $@

lex.yy.o: lex.yy.c funkcija.hpp
	$(CC) $(CFLAGS) -c $< -o $@

lex.yy.c: lexer.l parser.tab.hpp
	flex --nounput $<

parser.tab.o: parser.tab.cpp parser.tab.hpp funkcija.hpp tabela_simbola.hpp
	$(CC) $(CFLAGS) -c $< -o $@

parser.tab.cpp parser.tab.hpp: parser.ypp
	bison --header $<

funkcija.o: funkcija.cpp funkcija.hpp
	$(CC) $(CFLAGS) -c $< -o $@

tabela_simbola.o: tabela_simbola.cpp tabela_simbola.hpp
	$(CC) $(CFLAGS) -c $< -o $@

.PHONY: clean
clean:
	rm -f *.o parser lex.yy.c parser.tab.*

Након превођења и покретања над примером:

f = sin(x)
f'

f[1]
g = 1 + f(x*x)
g
g[0.5]


g'
g'[0.5]

Добијамо наредни излаз:

(cos(x)) * (1)
0.841471
(1) + (sin((x) * (x)))
1.2474
(0) + ((cos((x) * (x))) * (((1) * (x)) + ((x) * (1))))
0.968912
prihvaceno

Што је очекивани излаз—интерпретер ради!

Можемо још да га тестирамо за цурење меморије помоћу Valgrind-а. Ако се позиционирамо у одговарајући директоријум као на GitHub репозиторијуму, то можемо да урадимо командом:

valgrind ./parser < ../test

Синтаксно стабло

У другом делу задатка од нас се захтева да формирамо синтаксно стабло које може да се исписује и интерпретира. Ово радимо тако што:

задржавамо идентичну граматику и лексер који смо до сада записали (практично крећемо од стања parser.ypp фајла као после писања чистог парсера, пре писања интерпретера)
зато што је потребно да интерпретирамо стабло, користићемо све класе које смо писали за интерпретер, дакле, задржавамо све додатне класе које смо писали за интерпретацију
додајемо нове класе које представљају чворове синтаксног стабла тј. правимо фајлове sintaksno_stablo.hpp и sintaksno_stablo.cpp
додајемо акције у правила граматике која формирају стабло

Укратко, задржавамо већину ствари које смо већ написали, а остаје да направимо класе које представљају чворове синтаксног стабла и да додамо одговарјуће акције у већ написаним правилима граматике.

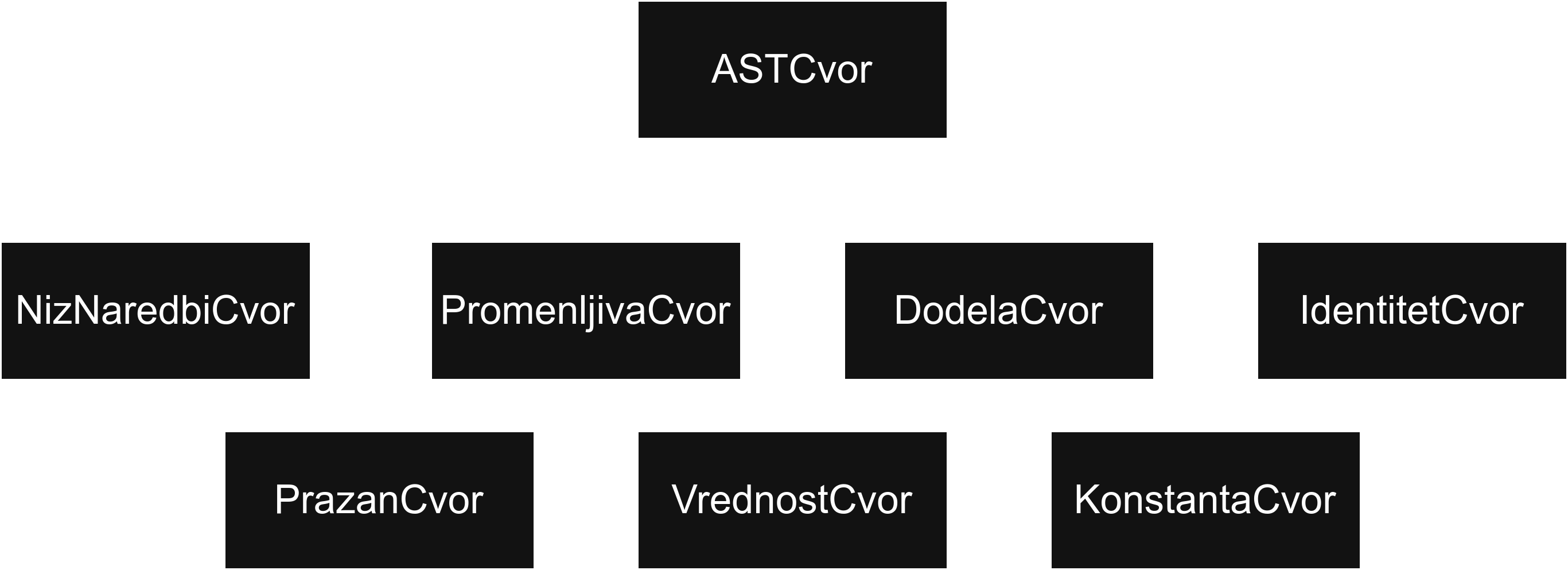
Крећемо са писањем класа чворова синтаксног стабла. Правимо сличну хијерархију као раније, на чијем се врху налази класа ASTCvor. Биће нам потребна по класа за сваки тип чвора, што ће практично бити по класа за свако правило у граматици. Поред тога, направићемо и апстрактне класе посреднике за чворове са тачно једним, односно тачно два детета (класе UnarniCvor и BinarniCvor).

Класе са тачно једним дететом ће бити следеће:

funkcije_sintaksno_stablo_unarnicvor

Са тачно два детета:

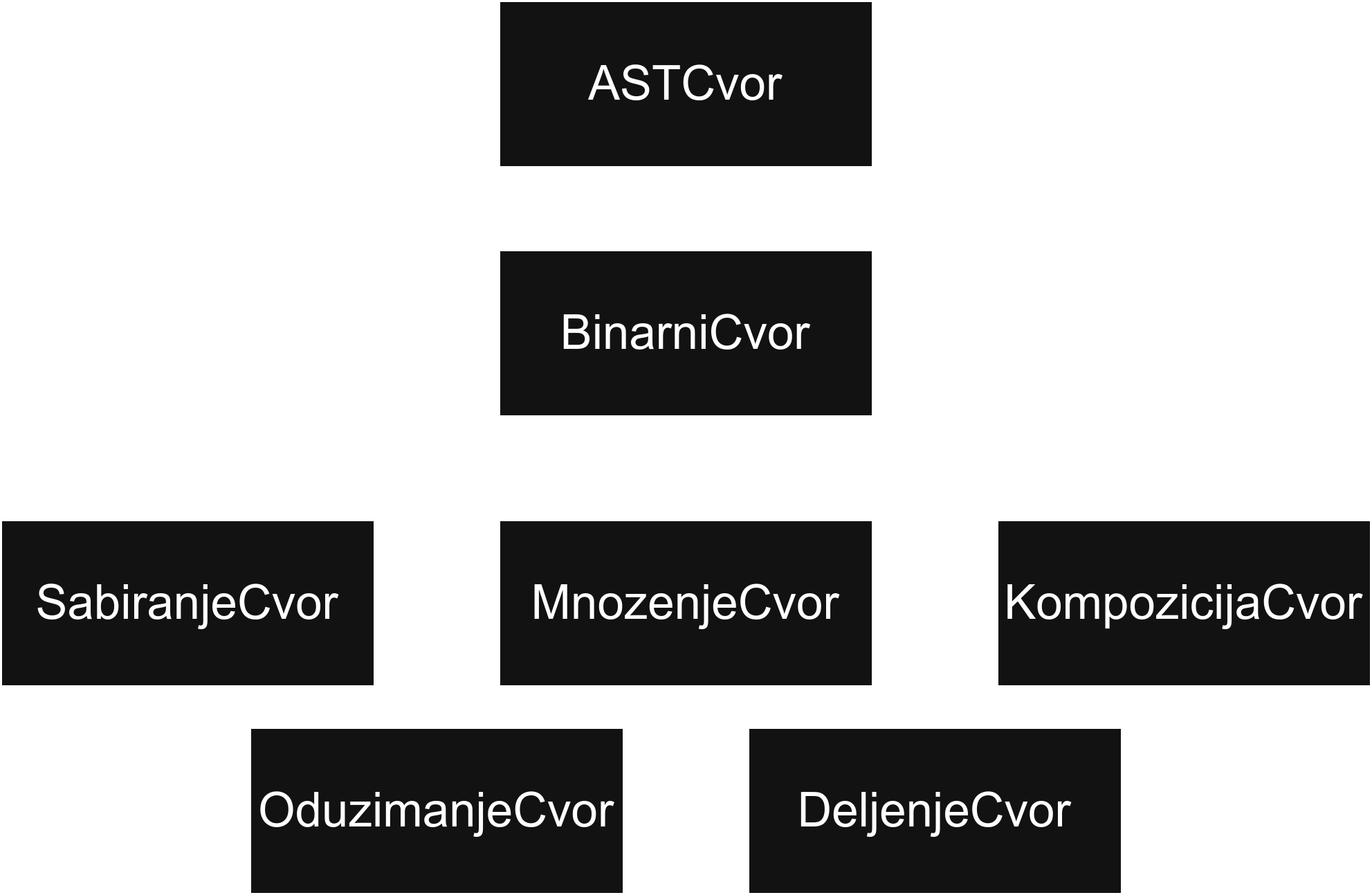
funkcije_sintaksno_stablo_binarnicvor

И преостале:

funkcija_sintaksno_stablo_01

У изради…

Додатак (shift и reduce акције)

Циљ овог додатка је да се детаљније опише процес парсирања у Bison-у. То је већ започето у поглављу како Bison извршава акције и пожељно је подсетити се тога пре читања даљег текста. Желимо да опишемо прецизније шта су то shift и reduce, као и како настају конфликти у граматици на (опет) површном нивоу, без улажења у детаље изгенерисаног потисног аутомата у позадини.

Нека нам је граматика језика иста као у остатку ове лекције и нека је, за почетак, на улазу реч

'(' izraz ')' '+' izraz

Поменули смо да се парсирање у позадини одвија навише, односно да парсер креће од речи са улаза и покушава да мења десне стране правила граматике левим. На мало детаљнијем нивоу, то се одвија приближно на следећи начин.

Парсер креће од речи и у чита је слева надесно. Из тог разлога, уведимо посебан симбол • (тачку) која ће означавати где је парсер стигао са читањем улаза (на пример, почетно стање би било представљено са • '(' izraz ')' '+' izraz). Поред тога, постојаће и један стек који ће се користити у позадини.

Током извршавања, парсер може да ради једну од две акције:

shift – чита наредни терминал/нетерминал са улаза (овим се помера тачка удесно, а прочитани симбол ставља на стек)
reduce – мења симболе са врха стека који чине десну страну неког правила граматике левом

Објаснимо то на примеру, симулацијом једног извршавања, које можемо да опишемо на следећи начин:

корак	стање	стек	акција
1.	`• '(' izraz ')' '+' izraz`		shift
2.	`'(' • izraz ')' '+' izraz`	`'('`	shift
3.	`'(' izraz • ')' '+' izraz`	`'(' izraz`	shift
4.	`'(' izraz ')' • '+' izraz`	`'(' izraz ')'`	reduce
5.	`'(' izraz ')' • '+' izraz`	`izraz`	shift
6.	`'(' izraz ')' '+' • izraz`	`izraz '+'`	shift
7.	`'(' izraz ')' '+' izraz •`	`izraz '+' izraz`	reduce
8.	`'(' izraz ')' '+' izraz •`	`izraz`	крај

На почетку, у првом кораку, нисмо још увек ништа прочитали, па је тачка скроз лево, а стек је празан. Једино што можемо да урадимо је да читамо даље, дакле, радимо shift.

У другом кораку, на стеку је '('. Међутим, то није десна страна ниједног правила, па не можемо да радимо reduce. Опет нам остаје само да читамо даље тј. да радимо shift.

У трећем кораку, на стеку имамо '(' izraz (стек читамо слева надесно и ово значи да је izraz на врху стека), што опет не представља десну страну неког правила. Можемо само да радимо shift.

Међутим, у 4. кораку на стеку се појављује '(' izraz ')' што јесте десна страна једног од правила. Зато у овом кораку можемо да радимо reduce. То значи да тачка остаје на истом месту, али се стек мења—сви симболи са врха који су чинили десну страну правила се склањају, а уместо њих, на врх стека, долази лева страна правила тј. на стеку ће се налазити izraz.

У 5. кораку на стеку немамо десну страну правила па радимо shift тј. додајемо на стек симбол '+'.

У 6. кораку на стеку имамо izraz '+', па само можемо да радимо shift чиме долазимо до краја улаза.

У 7. кораку нам се на стеку појавио izraz '+' izraz што можемо да мењамо, те радимо reduce.

Тиме добијамо на стеку аксиому, при чему је улаз прочитан до краја што је знак да смо завршили и да је реч прихваћена.

Приметимо да је ово само детаљнији опис који је већ виђен у делу са акцијама. Тамо смо рекли да се акције придружене правилима граматике у Bison-у извршавају када заменимо десне стране правила левим. Сада видимо да се оне заправо извршавају када парсер уради reduce. Заиста, читањем претходнох извођења уназад, и посматрањем само корака са reduce акцијама, можемо да формирамо стабло извођења које смо помињали раније.

Хајде да сада анализирамо пример који нам генерише Bison за конфликте у граматици (са опцијом -Wcounterexamples). Један од њих је:

parser.ypp: warning: shift/reduce conflict on token '\'' [-Wcounterexamples]
  Example: izraz '+' izraz • '\''
  Shift derivation
    izraz
    ↳ 7: izraz '+' izraz
                   ↳ 13: izraz • '\''
  Reduce derivation
    izraz
    ↳ 13: izraz                  '\''
          ↳ 7: izraz '+' izraz •

Већ смо поменули да су нам прве две линије најзначајније, јер нам говоре ком токену треба да доделимо приоритет и дају нам пример где конфликт настаје. Међутим, сада видимо и мало више. Bison при исписивању примера користи симбол • који има исто значење које смо и ми користили изнад—представља место до ког је парсер стигао са читањем улаза.

Анализирајмо ово извођење у претходном стилу.

корак	стање	стек	акција
1.	`• izraz '+' izraz '\''`		shift
2.	`izraz • '+' izraz '\''`	`izraz`	shift
3.	`izraz '+' • izraz '\''`	`izraz '+'`	shift
4.	`izraz '+' izraz • '\''`	`izraz '+' izraz`	?

Извршавање се одвија слично као и у претходном примеру, али овог пута када дођемо до 4. корака не знамо шта да радимо. Наиме, на врху стека се налази десна страна једног правила, али можемо и да читамо даље (тачка није дошла до краја улаза). Дакле, можемо да урадимо shift, али и reduce—имамо shift/reduce конфликт.

Ако се одлучимо за shift, извршавање се одвија овако:

4.	`izraz '+' izraz • '\''`	`izraz '+' izraz`	*shift*
5.	`izraz '+' izraz '\'' •`	`izraz '+' izraz '\''`	reduce
6.	`izraz '+' izraz '\'' •`	`izraz '+' izraz`	reduce
7.	`izraz '+' izraz '\'' •`	`izraz`	крај

У овом случају, настављамо даље читање и додајемо '\'' на стек. Када га додамо, онда на врху стека имамо izraz '\'' (приметимо да нам у овом тренутку није важан остатак стека) што је десна страна правила и радимо reduce. Тиме на стеку добијамо izraz '+' izraz и још једним reduce завршавамо парсирање.

Са друге стране, ако се у 4. кораку одлучимо за reduce, извођење изгледа овако:

4.	`izraz '+' izraz • '\''`	`izraz '+' izraz`	*reduce*
5.	`izraz '+' izraz • '\''`	`izraz`	shift
6.	`izraz '+' izraz '\'' •`	`izraz '\''`	reduce
7.	`izraz '+' izraz '\'' •`	`izraz`	крај

Зашто нисмо имали shift/reduce конфликт 4. кораку извођења у првом примеру? Шта би се догодило да је тада урађен shift? ¹

Дакле, парсирање може да се изврши на два различита начина, а тиме имамо и другачија стабла извођења. Ако бисмо пратили reduce кораке, првом (shift) извођењу одговара наредно стабло извођења:

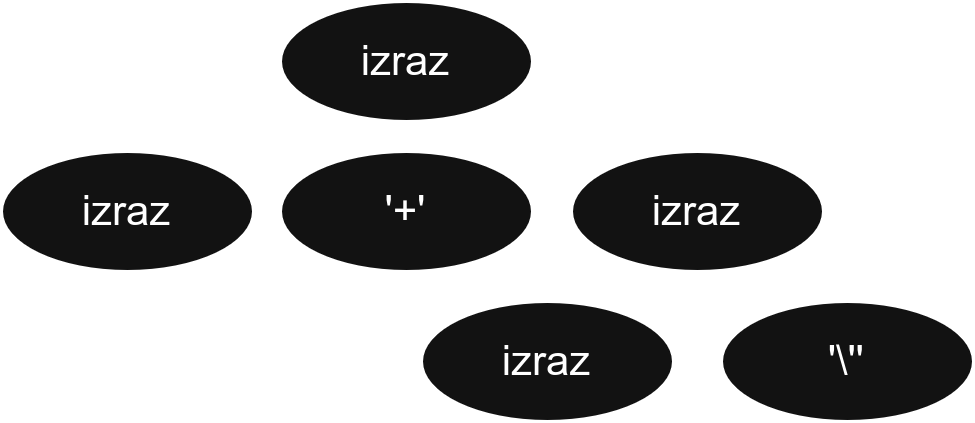
stablo_izvodjenja_shift

Док другом (reduce) извођењу одговара:

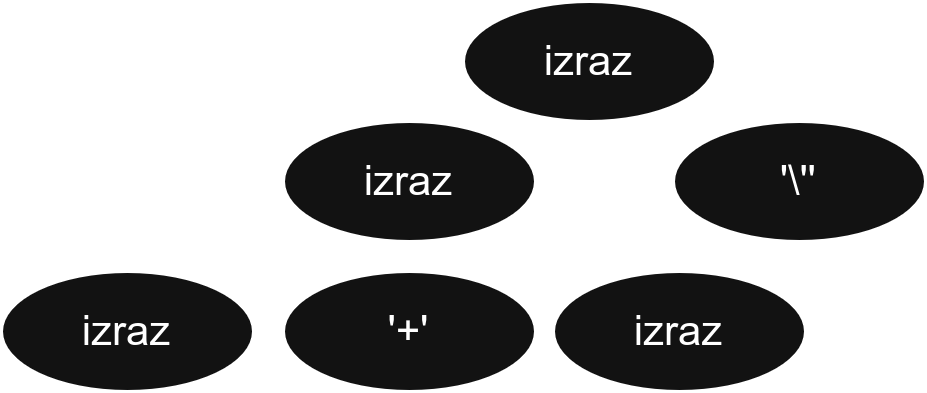
stablo_izvodjenja_reduce

Јасно видимо да ће од акције у 4. кораку извођења зависити приоритет оператора сабирања и извода.

Сада можемо и да протумачимо цео испис генератора контрапримера.

parser.ypp: warning: shift/reduce conflict on token '\'' [-Wcounterexamples]
  Example: izraz '+' izraz • '\''
  Shift derivation
    izraz
    ↳ 7: izraz '+' izraz
                   ↳ 13: izraz • '\''
  Reduce derivation
    izraz
    ↳ 13: izraz                  '\''
          ↳ 7: izraz '+' izraz •

Наиме, видимо за почетак да конфликт настаје када је тачка испред токена '\'', што смо и ми добили нашом анализом (у претходној терминологији, парсер је стигао до 4. корака). Поред тога исписана су нам и два могућа извођења: shift и reduce извођење и приказана стабла тих извођења.

Разрешавање конфликата

Да бисмо решили овај конфликт неопходно је да кажемо парсеру која акција има приоритет у случају конфликта. У овом случају желимо прво извођење, односно треба да означимо да shift има предност у односу на reduce.

Приоритет акција можемо да посматрамо на следећи начин²:

приоритет shift акције одређује приоритет токена који ће бити прочитан

(у овом случају, када се одради shift у 4. кораку, чита се токен '\'' тј. shift акција ће имати приоритет токена '\'')
приоритет reduce акције одређује приоритет правила које се користи приликом редуковања тј. правила чија се десна страна поклапа са врхом стека

(у овом случају, reduce у 4. кораку означава замену izraz '+' izraz са izraz тј. reduce акција ће имати приоритет правила izraz -> izraz '+' izraz)

При чему је приоритет правила једнак приоритету последњег токена који се у њему појављује (нпр. приоритет правила izraz -> izraz '+' izraz је једнак приоритету токена '+').

У овом конкретном примеру, желимо да се деси shift акција, чији је приоритет једнак приоритету одговарајућег токена који ће бити прочитан тј. токена '\'', у односу на reduce акцију чији је приоритет једнак приоритету правила izraz -> izraz '+' izraz тј. токена '+'.

Односно, потребно је да наведемо да токен '\'' има већи приоритет од токена '+', па у сегмент дефиниција додајемо:

parser.ypp

%left '+'
%right '\''

Што је управо што смо и радили у нашој граматици да разрешимо конфликте. Приметимо да се то поклапа са интуитивним схватањем да за разрешење приоритета између сабирања и извода, треба да дефинишемо приоритет токена '+' и '\''.

Међутим, интуиција није довољна у разешавању приоритета оператора [] и (), али претхода анализа једноставно објашњава како се тај проблем решава. Видели смо да Bison генерише следеће контрапримере.

parser.ypp: warning: shift/reduce conflict on token '[' [-Wcounterexamples]
  Example: izraz '+' izraz • '[' BROJ ']'

parser.ypp: warning: shift/reduce conflict on token '(' [-Wcounterexamples]
  Example: izraz '+' izraz • '(' izraz ')'

Дакле, парсер креће од • izraz '+' izraz '[' BROJ ']' и након три shift акције се налази у стању izraz '+' izraz • '[' BROJ ']' где на располагању има две могућности: да ради shift (чита токен '[') или да ради reduce (по правилу izraz -> izraz '+' izraz).

Сада знамо да бисмо разрешили конфликт тј. да бисмо дали предност оператору [], треба да дамо предност shift акцији у односу на reduce. Shift има приоритет који је једнак приоритету токена '[', док reduce има приоритет одговарајућег правила, дакле, последњег токена у том правилу, што је токен '+'.

Зато је за разрешавање довољно додати у сегменту дефиниција:

parser.ypp

%left '+'
%precedence '['

Што се поклапа са оним што смо урадили иницијално у парсер фајлу. Слично ситуација је код оператора ().

Попут shift/reduce конфликата, могу се јавити и reduce/reduce конфликти. Тада парсер може да ради reduce акцију по два различита правила и то је најчешће знак да нам граматика није добро написана и да је потребно преправити постојећа правила.

Да смо се одлучили за shift у 4. кораку извођења, на стек бисмо додали '+', а потом izraz и добили на крају '(' izraz ')' '+' izraz. Међутим, ни у једном тренутку се на врху стека не би нашла десна страна неког правила и дошли бисмо до краја улаза, али на стеку не би остала аксиома. Дакле, не бисмо могли да завршимо извођење. Овде се поставља још једно питање: како парсер зна да не може да уради на том месту shift, док у другом примеру види да може и shift и reduce? Одговор лежи у оном делу који овде прећутно прелазимо, а то је рад LALR парсера. ↩
Детаљи се могу пронаћи у званичној документацији Bison-а. Поред поменутог, у документацији се могу пронаћи и повезани чланци који употпуњују ову причу. ↩

Поставка проблема

Парсер

Граматика језика

Shift/reduce конфликти

Лексер

Повезивање

Интерпретација

Класа Funkcija

Класа KonstantnaFunkcija

Класа IdentitetFunkcija

Класа UnarnaFunkcija

Класа NegacijaFunkcija

Класа SinFunkcija

Класа CosFunkcija

Класа BinarnaFunkcija

Класа SabiranjeFunkcija

Класа OduzimanjeFunkcija

Класа MnozenjeFunkcija

Класа DeljenjeFunkcija

Акције у Bison-у

Класа TabelaSimbola

Акције

Синтаксно стабло

Додатак (shift и reduce акције)

Разрешавање конфликата

Класа `Funkcija`

Класа `KonstantnaFunkcija`

Класа `IdentitetFunkcija`

Класа `UnarnaFunkcija`

Класа `NegacijaFunkcija`

Класа `SinFunkcija`

Класа `CosFunkcija`

Класа `BinarnaFunkcija`

Класа `SabiranjeFunkcija`

Класа `OduzimanjeFunkcija`

Класа `MnozenjeFunkcija`

Класа `DeljenjeFunkcija`

Класа `TabelaSimbola`