U narednom apletu se prikazuje presek dva konveksna mnogougla. Pomeranjem temena mnogouglova, presek se automatski ažurira.
Direktno rešenje
Jedno moguće direktno rešenje se može zasnovati na različitim algoritmima koje smo do sada opisali. Presek dva konveksna mnogougla je konveksni mnogougao čiji se skup temena sastoji od:
- temena prvog mnogougla koje pripadaju unutrašnjosti drugog (zatvorenog) mnogougla,
- temena drugog mnogougla koje pripadaju unutrašnjosti prvog (zatvorenog) mnogougla,
- presečnih tačaka stranica mnogouglova.
Kada se odrede sva temena u ova tri skupa, potrebno ih je urediti, što se može uraditi, na primer, sortiranjem na osnovu ugla koji poluprava koja spaja težište rezultujućeg mnogougla sa trenutnim temenom zaklapa sa pozitivnim smerom \(x\)-ose (pošto su sva temena poznata, težište se lako izračunava izračunavanjem aritmetičke sredine njihovih koordinata).
Za svaku tačku mnogouglova možemo pokrenuti proveru pripadnosti drugom mnogouglu, čija je složenost, u slučaju konveksnih mnogouglova, logaritamska. Stoga je za određivanje prva dva skupa temena potrebno vreme \(O(m\log{n} + n\log{m})\). Da bi se odredili preseci stranica, možemo algoritam za određivanje preseka dve duži primeniti na sve parove stranica dva mnogougla, za šta je potrebno vreme \(O(mn)\). Broj parova duži koje se ispituju je moguće smanjiti tako što se ispituju samo duži čija su temena takva da jedno pripada, a drugo ne pripada mnogouglu. Ipak, u nastavku ćemo videti da postoji i algoritam linearne složenosti \(O(m+n)\) za određivanje preseka dva mnogougla, pa ovaj algoritam nećemo dalje razrađivati.
Efikasan algoritam
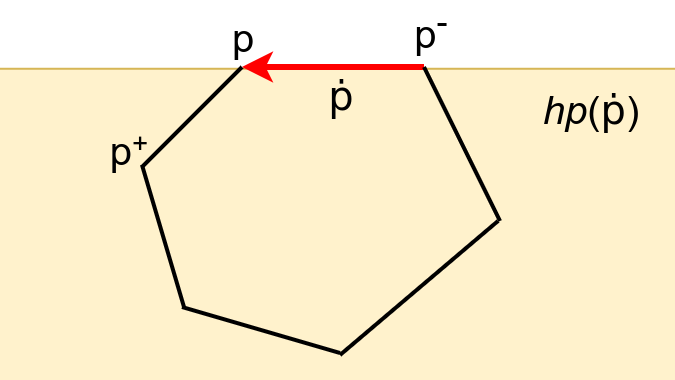
Jedan efikasan algoritam za određivanje preseka dva konveksna mnogougla su opisali O Rurk, Čin, Olson i Nador. Algoritam je zasnovan na tehnici dva pokazivača. Pokazivač \(p\) obilazi mnogougao \(P\) u pozitivnom matematičkom smeru, a pokazivač \(q\) obilazi mnogougao \(Q\) u pozitivnom smeru. Sa \(p^-\), \(p\) i \(p^+\) biće obeležene redom prethodna, tekuća i sledeća tačka mnogougla \(P\). Položajem pokazivača \(p\) određena je tekuća stranica mnogougla, tj. usmerena duž \(p^{-}p\) koja predstavlja tu tekuću stranicu, a koja je uvek usmerena u pozitivnom smeru tj. tako da joj se mnogougao nalazi sa leve strane (slika 1). Vrh te duži je tačka \(p\), dno joj je tačka \(p^{-}\), dok ćemo samu duž obeležiti sa \(\dot{p}\). Sa \(\mathit{hp}(\dot{p})\) ćemo obeležiti poluravan čija je ivica prava koja sadrži \(\dot{p}\), i koja sadrži mnogouao \(P\) (tj. nalazi se levo od \(\dot{p}\)). Proizvoljna tačka \(m\) pripada poluravni \(\mathit{hp}(\dot{p})\) ako i samo ako je \(\overrightarrow{p^-p}\times_{2d}\overrightarrow{p^-m} \geq 0\). Analogne oznake koristimo i za \(q\).
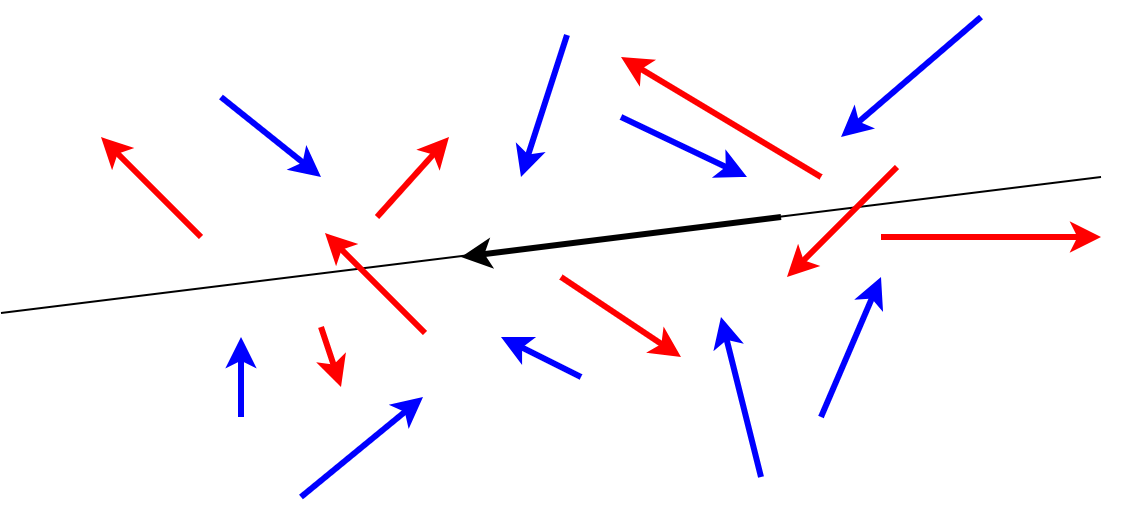
Intuitivno je jasno kada usmerena duž ukazuje ka pravoj, a kada ukazuje od nje (slika 2). Ovo se može i precizirati. Vektor \(\dot{p}\) ukazuje prema pravoj na kojoj leži \(\dot{q}\) ako i samo ako je \(p\in \mathit{hp}(\dot{q})\) i \(\dot{q}\times_{2d} \dot{p} < 0\) ili \(p\notin \mathit{hp}(\dot{q})\) i \(\dot{q}\times_{2d} \dot{p} \geq 0\) (ako je ta prava horizontalna, a duž \(q\) usmerena na levo, kao na slici, tada ovo znači da je duž \(\dot{p}\) usmerena na gore i vrh joj je u poluravni ispod prave ili je usmerena na dole i vrh joj je u poluravni iznad prave).
Pokazivači se pomeraju tako da se garantuje da će se tokom njihovog pomeranja pronaći svi preseci stranica. U svakom koraku algoritma se proverava da li se duži \(\dot{p}\) i \(\dot{q}\) seku i ako se seku, presečna tačka se dodaje rezultujućem mnogouglu. Nakon toga se pomera jedan od dva pokazivača. Razmotrimo razne mogućnosti za usmerene duži \(\dot{p}\) i \(\dot{q}\).
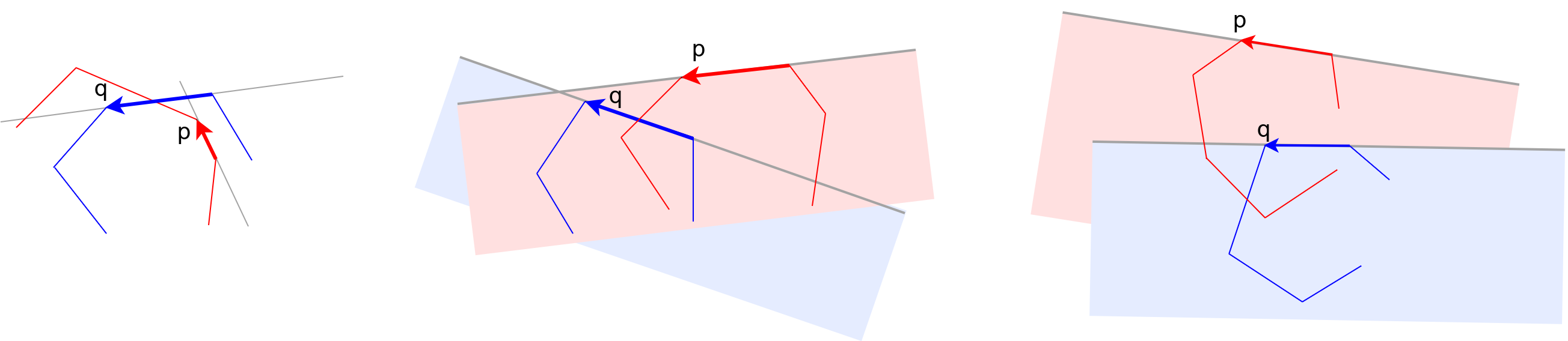
Moguće je da duž \(\dot{p}\) ukazuje ka pravoj na kojoj leži \(\dot{q}\), a da duž \(\dot{q}\) ne ukazuje ka pravoj na kojoj leži \(\dot{p}\) (slika 3, levo). U tom slučaju pomeramo pokazivač \(p\), u cilju da u nekom trenutku duž \(\dot{p}\) preseče pravu na kojoj leži \(\dot{q}\) (ivicu poluravni \(\mathit{hp}(\dot{q})\)) i dođe do poluravni \(\mathit{hp}(\dot{q})\) u kojoj leži mnogougao \(Q\), pa i svi preseci koje treba pronaći. Slučaj kada \(\dot{q}\) ukazuje ka pravoj na kojoj leži \(\dot{p}\), a \(\dot{p}\) ne ukazuje ka pravoj na kojoj leži \(\dot{q}\) se obrađuje analogno.
Moguće je da obe duži \(\dot{p}\) i \(\dot{q}\) ukazuju ka pravama na kojoj leži ona druga (slika 3, sredina). U tom slučaju, zbog konveksnosti mora da važi da tačno jedna od tačaka \(p\) ili \(q\) pripada poluravni kojoj je granica prava na kojoj leži druga duž i u kojoj se nalazi njoj odgovarajući mnogougao. U primeru na slici tačka \(p\) ne pripada poluravni \(\mathit{hp}(\dot{q})\), određenom pravom na kojoj je duž \(\dot{q}\) i u kojoj se nalazi mnogougao \(Q\), dok tačka \(q\) pripada poluravni \(\mathit{hp}(\dot{p})\) određenom pravom na kojoj je duž \(\dot{p}\) i u kojoj se nalazi mnogougao \(Q\). Da bi duž \(\dot{p}\) sekla neku stranicu mnogougla \(Q\), potrebno je da tačka \(p\) pripada unutrašnjosti mnogougla \(Q\), pa samim tim i poluravni \(\mathit{hp}(\dot{q})\). Analogno važi i za \(\dot{q}\) i \(P\). Zato se u ovom slučaju pomera onaj pokazivač koji odgovara tački koja ne pripada unutrašnjosti odgovarajuće poluravni.
Moguće je i da nijedna duž ne ukazuje ka pravoj na kojoj leži ona druga (slika 3, desno). I u tom slučaju zbog konveksnosti mora da važi da tačno jedna od tačaka \(p\) tj. \(q\) pripada unutrašnjosti mnogougla \(Q\) tj. \(P\) i ponovo je potrebno pomeriti onu koja ne pripada unutrašnjosti odgovarajuće poluravni.
Dakle, kada god tačno jedna od dve usmerene duži ukazuje ka pravoj na kojoj leži ona druga, nju pomeramo, dok u ostalim slučajevima pomeramo vrh one duži koji ne leži u unutrašnjosti poluravni sa leve strane prave određene drugom duži.
Algoritam se može zaustaviti kada se ceo presečni mnogougao kompletira tj. kada se poslednji pronađeni presek duži poklopi sa prvim pronađenim presekom (preseci će biti određeni redom, u pozitivnom smeru). Međutim, ako preseci stranica ne postoje, pokazivači će se neprestano pomerati. Dokazuje se da se nakon najviše \(2(|P|+|Q|)\) koraka pronalaze svi preseci stranica, tako da se algoritam može zaustaviti i ako se nakon \(2(|P|+|Q|)\) ne pronađe nijedna presečna tačka. U tom slučaju, ako \(p\) pripada unutrašnjosti \(Q\), presek je ceo mnogougao \(P\), ako \(q\) pripada unutrašnjosti \(P\), presek je ceo mnogougao \(Q\), dok se u suprotnom se mnogouglovi ne seku.
U narednom apletu se prikazuje kretanje dva pokazivača tokom izvršavanja algoritma.
U prethodnom opisu je pretpostavljeno da ne postoje degenerisani slučajevi, tj. da se temena mnogouglova ne poklapaju, da nijedno teme jednog ne pripada stranici drugog mnogougla niti da se stranice mnogouglova poklapaju. I ovi slučajevi se mogu ispravno obraditi ako se algoritam malo prilagodi. Prvo, za dve kolinearne duži (kada je \(\dot{p} \times \dot{q} = 0\)) se uvek smatra da se ne seku. Drugo, kriterijum zaustavljanja treba prilagoditi. Naime, kada stranica sadrži teme, može se dogoditi da se isti presek nađe i nakon pomeranja pokazivača. Zato se može desiti da se algoritam zaustavi jer će drugi pronađeni presek biti jednak prvom. Stoga se algoritam može zaustaviti kada je tekući presek jednak prvom pronađenom, ali pod uslovom da taj prvi presek nije pronađen u prethodnom koraku algoritma.
double uPoluravni(const Tacka& A, const Tacka& B, const Tacka& M) {
Vektor AB = vektor(A, B);
Vektor AM = vektor(A, M);
return vektorski_proizvod(AB, AM) >= 0;
}
vector<Tacka> presekMnouglova(const vector<Tacka>& P, const vector<Tacka>& Q) {
int m = P.size(), n = Q.size();
vector<Tacka> presek;
// dva pokazivaca
int pm = 0, p = 1;
int qm = 0, q = 1;
// ili P[p] pripada poluravni hp(Q[qm]Q[q])
// ili Q[q] pripada poluravni hp(P[pm]P[p])
// ovom promenljivom registrujemo za koju od tacaka p ili q je to vazilo
// prilikom pronalaska prethodnog preseka
char unutra = ' ';
// presecna tacka nadjena u prethodnom koraku (mozda i nije postojao presek)
Tacka prethodniPresek;
bool postojiPrethodniPresek = false;
for (int i = 0; i <= 2*(m + n); i++) {
Tacka M;
// proveravamo da li se duzi seku
if (presekDuzi(P[pm], P[p], Q[qm], Q[q], M)) {
if (presek.size() > 0) {
// vratili smo se na pocetnu tacku i zatvorili ceo presecni mnogougao
// presek nije pronadjen u prethodnom koraku
if (M == presek[0] && (!postojiPrethodniPresek || M != prethodniPresek))
return presek;
}
// nasli smo novu presecnu tacku i dodajemo je u presecni mnogougao
if (presek.empty() || M != presek.back())
presek.push_back(M);
// pripremamo se za naredni korak tako sto pamtimo tekuci presek
prethodniPresek = M;
postojiPrethodniPresek = true;
// pamtimo da li p pripada poluravni hp(q.) ili q pripada poluravni hp(p.)
if (uPoluravni(Q[qm], Q[q], P[p]))
unutra = 'P';
else
unutra = 'Q';
} else
// pripremamo se za naredni korak tako sto belezimo da nije bilo preseka
postojiPrethodniPresek = false;
// funkcija kojom se pomera pokazivac p
auto pomeriP =
[&](){
// ako je poslednji presek P[p] pripadao poluravni hp(Q[qm]Q[q]),
// onda je tekuce P[p] deo presecnog mnogougla
if (unutra == 'P' && (presek.empty() || P[p] != presek.back()))
presek.push_back(P[p]);
// pomeramo se na sledecu tacku mnogougla P
pm = p;
p = (p + 1) % m;
};
// funkcija kojom se pomera pokazivac q
auto pomeriQ =
[&](){
// ako je poslednji presek Q[q] pripadao poluravni hp(P[pm]P[p]),
// onda je tekuce Q[q] deo presecnog mnogougla
if (unutra == 'Q' && (presek.empty() || Q[q] != presek.back()))
presek.push_back(Q[q]);
// pomeramo se na sledecu tacku mnogougla Q
qm = q;
q = (q + 1) % m;
};
Vektor pdot = vektor(P[pm], P[p]);
Vektor qdot = vektor(Q[qm], Q[q]);
if (vektorski_proizvod(qdot, pdot) >= 0) {
if (uPoluravni(Q[qm], Q[q], P[p])) {
// pdot nije usmeren ka qdot i P[p] pripada poluravni hp(qdot)
// q treba pomeriti:
// i ako qdot jeste usmeren ka pdot (jer je jedini usmeren)
// i ako qdot nije usmeren ka pdot (jer se pomera tacka
// koja ne pripada poluravni, a to je Q[q])
pomeriQ();
} else {
// pdot je usmeren ka qdot i P[p] ne pripada poluravni hp(qdot)
// p treba pomeriti:
// i ako qdot nije usmeren ka pdot (jer je pdot jedini usmeren)
// i ako qdot jeste usmeren ka pdot (jer se pomera tacka
// koja ne pripada poluravni, a to je P[p])
pomeriP();
}
} else {
if (uPoluravni(P[pm], P[p], Q[q])) {
// qdot nije usmeren ka pdot i Q[q] pripada poluravni hp(pdot)
// p treba pomeriti
// i ako pdot jeste usmeren ka qdot (jer je pdot jedini usmeren)
// i ako pdot nije usmeren ka qdot (jer se pomera tacka
// koja ne pripada poluravni, a to je P[p])
pomeriP();
}
else {
// qdot jeste usmeren ka pdot i Q[q] ne pripada poluravni hp(pdot)
// q treba pomeriti
// i ako pdot nije usmeren ka qdot (jer je qdot jedini usmeren)
// i ako pdot jeste usmeren ka qdot (jer se pomera tacka
// koja ne pripada poluravni, a to je Q[q])
pomeriQ();
}
}
}
// ili je presek prazan, ili je P sadrzan u Q ili je Q sadrzan u P
if (uMnogouglu(Q[0], P))
// Q je sadrzan u P
presek = Q;
else if (uMnogouglu(P[0], Q))
// P je sadrzan u Q
presek = P;
return presek;
}#include <iostream>
#include <iomanip>
#include <vector>
using namespace std;
struct Tacka {
double x, y;
bool operator==(const Tacka& T) const{
return x == T.x && y == T.y;
}
bool operator!=(const Tacka& T) const{
return !(*this == T);
}
};
struct Vektor {
double x, y;
};
double vektorski_proizvod(const Vektor& a, const Vektor& b) {
return a.x * b.y - a.y * b.x;
}
Vektor vektor(const Tacka& A, const Tacka& B) {
Vektor v;
v.x = B.x - A.x;
v.y = B.y - A.y;
return v;
}
bool presekDuzi(const Tacka& A, const Tacka& B,
const Tacka& M, const Tacka& N,
Tacka& P) {
Vektor AB = vektor(A, B);
Vektor MN = vektor(M, N);
Vektor MA = vektor(M, A);
double ABMN = vektorski_proizvod(AB, MN);
// smatramo da se kolinearne duzi ne seku
if (ABMN == 0)
return false;
double k1 = vektorski_proizvod(AB, MA) / ABMN;
double k2 = -vektorski_proizvod(MA, MN) / ABMN;
if (0 <= k1 && k1 <= 1 && 0 <= k2 && k2 <= 1) {
P.x = M.x + k1 * MN.x;
P.y = M.y + k1 * MN.y;
return true;
} else
return false;
}
bool uMnogouglu(const Tacka& M, const vector<Tacka>& temena) {
int n = temena.size();
for (int i = 0; i < n; i++) {
const Tacka& P = temena[i];
const Tacka& Q = temena[(i + 1) % n];
const Tacka& R = temena[(i + 2) % n];
Vektor PQ = vektor(P, Q);
Vektor QR = vektor(Q, R);
Vektor QM = vektor(Q, M);
if (vektorski_proizvod(PQ, QR) * vektorski_proizvod(PQ, QM) < 0)
return false;
}
return true;
}
double uPoluravni(const Tacka& A, const Tacka& B, const Tacka& M) {
Vektor AB = vektor(A, B);
Vektor AM = vektor(A, M);
return vektorski_proizvod(AB, AM) >= 0;
}
vector<Tacka> presekMnouglova(const vector<Tacka>& P, const vector<Tacka>& Q) {
int m = P.size(), n = Q.size();
vector<Tacka> presek;
// dva pokazivaca
int pm = 0, p = 1;
int qm = 0, q = 1;
// ili P[p] pripada poluravni hp(Q[qm]Q[q])
// ili Q[q] pripada poluravni hp(P[pm]P[p])
// ovom promenljivom registrujemo za koju od tacaka p ili q je to vazilo
// prilikom pronalaska prethodnog preseka
char unutra = ' ';
// presecna tacka nadjena u prethodnom koraku (mozda i nije postojao presek)
Tacka prethodniPresek;
bool postojiPrethodniPresek = false;
for (int i = 0; i <= 2*(m + n); i++) {
Tacka M;
// proveravamo da li se duzi seku
if (presekDuzi(P[pm], P[p], Q[qm], Q[q], M)) {
if (presek.size() > 0) {
// vratili smo se na pocetnu tacku i zatvorili ceo presecni mnogougao
// presek nije pronadjen u prethodnom koraku
if (M == presek[0] && (!postojiPrethodniPresek || M != prethodniPresek))
return presek;
}
// nasli smo novu presecnu tacku i dodajemo je u presecni mnogougao
if (presek.empty() || M != presek.back())
presek.push_back(M);
// pripremamo se za naredni korak tako sto pamtimo tekuci presek
prethodniPresek = M;
postojiPrethodniPresek = true;
// pamtimo da li p pripada poluravni hp(q.) ili q pripada poluravni hp(p.)
if (uPoluravni(Q[qm], Q[q], P[p]))
unutra = 'P';
else
unutra = 'Q';
} else
// pripremamo se za naredni korak tako sto belezimo da nije bilo preseka
postojiPrethodniPresek = false;
// funkcija kojom se pomera pokazivac p
auto pomeriP =
[&](){
// ako je poslednji presek P[p] pripadao poluravni hp(Q[qm]Q[q]),
// onda je tekuce P[p] deo presecnog mnogougla
if (unutra == 'P' && (presek.empty() || P[p] != presek.back()))
presek.push_back(P[p]);
// pomeramo se na sledecu tacku mnogougla P
pm = p;
p = (p + 1) % m;
};
// funkcija kojom se pomera pokazivac q
auto pomeriQ =
[&](){
// ako je poslednji presek Q[q] pripadao poluravni hp(P[pm]P[p]),
// onda je tekuce Q[q] deo presecnog mnogougla
if (unutra == 'Q' && (presek.empty() || Q[q] != presek.back()))
presek.push_back(Q[q]);
// pomeramo se na sledecu tacku mnogougla Q
qm = q;
q = (q + 1) % m;
};
Vektor pdot = vektor(P[pm], P[p]);
Vektor qdot = vektor(Q[qm], Q[q]);
if (vektorski_proizvod(qdot, pdot) >= 0) {
if (uPoluravni(Q[qm], Q[q], P[p])) {
// pdot nije usmeren ka qdot i P[p] pripada poluravni hp(qdot)
// q treba pomeriti:
// i ako qdot jeste usmeren ka pdot (jer je jedini usmeren)
// i ako qdot nije usmeren ka pdot (jer se pomera tacka
// koja ne pripada poluravni, a to je Q[q])
pomeriQ();
} else {
// pdot je usmeren ka qdot i P[p] ne pripada poluravni hp(qdot)
// p treba pomeriti:
// i ako qdot nije usmeren ka pdot (jer je pdot jedini usmeren)
// i ako qdot jeste usmeren ka pdot (jer se pomera tacka
// koja ne pripada poluravni, a to je P[p])
pomeriP();
}
} else {
if (uPoluravni(P[pm], P[p], Q[q])) {
// qdot nije usmeren ka pdot i Q[q] pripada poluravni hp(pdot)
// p treba pomeriti
// i ako pdot jeste usmeren ka qdot (jer je pdot jedini usmeren)
// i ako pdot nije usmeren ka qdot (jer se pomera tacka
// koja ne pripada poluravni, a to je P[p])
pomeriP();
}
else {
// qdot jeste usmeren ka pdot i Q[q] ne pripada poluravni hp(pdot)
// q treba pomeriti
// i ako pdot nije usmeren ka qdot (jer je qdot jedini usmeren)
// i ako pdot jeste usmeren ka qdot (jer se pomera tacka
// koja ne pripada poluravni, a to je Q[q])
pomeriQ();
}
}
}
// ili je presek prazan, ili je P sadrzan u Q ili je Q sadrzan u P
if (uMnogouglu(Q[0], P))
// Q je sadrzan u P
presek = Q;
else if (uMnogouglu(P[0], Q))
// P je sadrzan u Q
presek = P;
return presek;
}
vector<Tacka> unesiMnogougao() {
int m;
cin >> m;
vector<Tacka> P(m);
for (int i = 0; i < m; i++)
cin >> P[i].x;
for (int i = 0; i < m; i++)
cin >> P[i].y;
return P;
}
void ispisiMnogougao(const vector<Tacka>& R) {
cout << R.size() << endl;
cout << fixed << showpoint << setprecision(5);
for (int i = 0; i < R.size(); i++)
cout << R[i].x << " ";
cout << endl;
for (int i = 0; i < R.size(); i++)
cout << R[i].y << " ";
cout << endl;
}
int main() {
vector<Tacka> P = unesiMnogougao();
vector<Tacka> Q = unesiMnogougao();
vector<Tacka> R = presekMnouglova(P, Q);
ispisiMnogougao(R);
return 0;
}