Korensko drvo

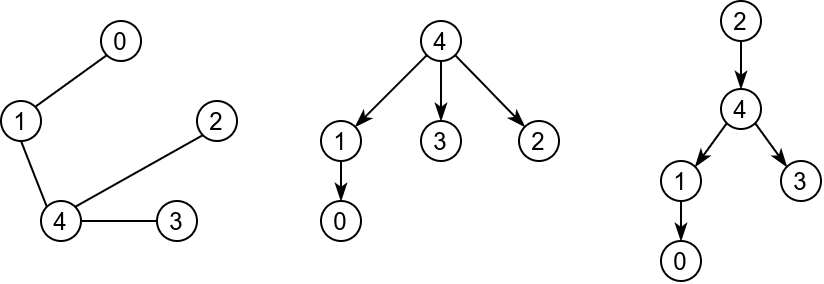
Povezan graf koji sadrži \(n\) čvorova i \(n-1\) grana se naziva drvo. Svaki čvor drveta može biti njegov koren. Napiši program koji za dato drvo i dati koren određuje smer svih grana u tom korenskom drvetu.

Opis ulaza

Sa standardnog ulaza se unosi broj čvorova \(n\) (\(1 \leq n \leq 10^5\)), a zatim i opis \(n-1\) grana drveta. Svaka grana je određena brojevima polaznog i završnog čvora (celi brojevi između \(0\) i \(n-1\)), pri čemu su oni zadati u proizvoljnom redosledu. U poslednjem redu se nalazi redni broj korena (broj između \(0\) i \(n-1\)).

Opis izlaza

Na standardni izlaz treba ispisati grane rezultujućeg korenskog drveta, pri čemu svaka grana treba da bude orijentisana u smeru od korena ka listovima. Niz svih grana (parova brojeva) treba da bude leksikografski sortiran (grane se porede prvo po prvom, a zatim po drugom čvoru).

Primer 1

Ulaz

5
1 0
2 4
3 4
4 1
4

Izlaz

1 0
4 1
4 2
4 3

Primer 2

Ulaz

5
1 0
2 4
3 4
4 1
2

Izlaz

1 0
2 4
4 1
4 3

Objašnjenje

Na slici je prikaza graf i dva korenska drveta koja odgovaraju primerima

Rešenje

Zadatak se može jednostavno rešiti tako što se pokrene algoritam pretrage u dubinu krenuvši od početnog čvora. Svaka pretraga u dubinu povezanog grafa implicitno generiše jedno korensko drvo (gde su grane određene prelazima sa čvora na njegove neposećene susede) i u našem zadatku to je upravo drvo koje je potrebno generisati.

#include <iostream>
#include <vector>
#include <utility>
#include <stack>
#include <algorithm>

using namespace std;

class Graph {
private:
  int number_of_nodes;
  vector<vector<int>> neighbours_list;
  vector<bool> visited;

public:
  Graph(int number_of_nodes) {
    this->number_of_nodes = number_of_nodes;
    visited.resize(number_of_nodes, false);
  }

  void add_edge(int u, int v) {
    neighbours_list[u].push_back(v);
    neighbours_list[v].push_back(u);
  }

  vector<pair<int, int>> create_tree(int root) {
    vector<pair<int, int>> edges;
    edges.reserve(number_of_nodes - 1);

    stack<int> s;
    s.push(root);
    visited[root] = true;

    int current;
    while (!s.empty()) {
      current = s.top();
      s.pop();

      for (int neighbour : neighbours_list[current])
        if (!visited[neighbour]) {
          s.push(neighbour);
          visited[neighbour] = true;
          edges.emplace_back(current, neighbour);
        }
    }

    sort(begin(edges), end(edges));
    return edges;
  }
};

int main() {

  int number_of_nodes;
  cin >> number_of_nodes;

  Graph *G = new Graph(number_of_nodes);

  int u, v;
  for (int i = 0; i < number_of_nodes - 1; i++) {
    cin >> u >> v;
    G->add_edge(u, v);
  }

  int root;
  cin >> root;

  vector<pair<int, int>> edges = G->create_tree(root);
  for (const auto &p : edges) {
    cout << p.first << " " << p.second << "\n";
  }

  delete G;
  return 0;
}