Opis naivnog rešenja
Za svaki pomeraj \((s, l) \in \{(i, j) : 1 \leq 1 \leq n - m + 1, 1 \leq j \leq n - m + 1\}\) proverimo da li \(P[1..m, 1..m] = T[s+1..s+m, l+1..s+m]\). Složenost jedne provere \(P[1..m, 1..m] = T[s+1..s+m, l+1..s+m]\) je \(O(m^2)\), a kako imamo ukupno \((n - m + 1)^2\) ovakvih provera, složenost algoritma je \(O((nm)^2)\).
#include <iostream>
#include <vector>
using namespace std;
bool check(const vector<vector<char>> &text,
const vector<vector<char>> &pattern,
const int s, const int l)
{
const int m = pattern.size();
for (int i = 0; i < m; i++) {
for (int j = 0; j < m; j++) {
if (text[s + i][l + j] != pattern[i][j]) {
return false;
}
}
}
return true;
}
bool naive_matcher(const vector<vector<char>> &text,
const vector<vector<char>> &pattern)
{
const int n = text.size();
const int m = pattern.size();
for (int s = 0; s < n - m + 1; s++) {
for (int l = 0; l < n - m + 1; l++) {
if (check(text, pattern, s, l)) {
return true;
}
}
}
return false;
}
int main(void)
{
int n, m;
std::cin >> n >> m;
vector<vector<char>> text(n, vector<char> (n));
vector<vector<char>> pattern(m, vector<char> (m));
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
cin >> text[i][j];
}
}
for (int i = 0; i < m; i++) {
for (int j = 0; j < m; j++) {
cin >> pattern[i][j];
}
}
if (naive_matcher(text, pattern)) {
cout << "da" << endl;
} else {
cout << "ne" << endl;
}
return 0;
}Opis glavnog rešenja
Bolje rešenje se dobija primenom generalizacije Rabin-Karpovog algoritma na dve dimenzije. U originalnom algoritmu, računamo heš vrednost niske i heš vrednosti segmenata teksta koje onda upoređujemo. U ovom zadatku, računaćemo haš vrednost \(p\) matrice \(P[1..m, 1..m]\) i heš vrednosti \(t_{s,l}\) segmenata \(T[s+1..s+m, l+1..l+m]\). Kao i u originalnom algortmu, ako \(p \neq t_{s, l}\), onda sigurno \(P[1..m, 1..m] \neq T[s+1..s+m, l+1..l+m]\), a ako \(p = t_{s, l}\), onda moramo proveriti da li \(P[1..m, 1..m] = T[s+1..s+m, l+1..l+m]\) (ovu proveru izvršavamo kao i u naivnom algorimu i ona je složenosti \(O(m^2)\)).
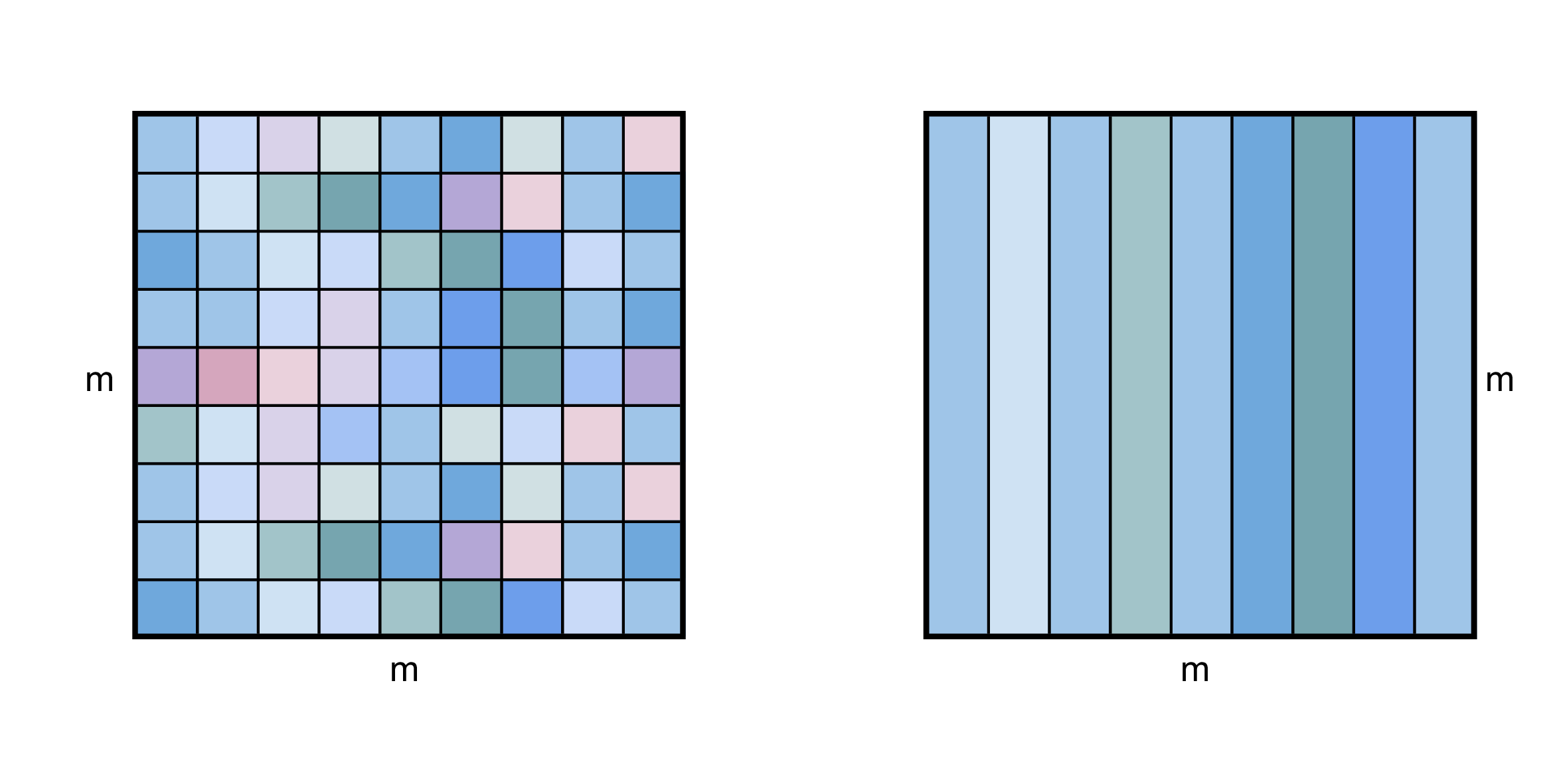
Dalje, diskutujemo o tome kako izračunati haš vrednosti \(p\) i \(t_{s, 0}\), kao i način na koji možemo izračunati \(t_{s, l+1}\) ukoliko znamo \(t_{s, l}\). Heš vrednost \(p\) možemo dobiti tako što najpre izračunamo heš vrednosti kolona matrice \(P[1..m, 1..m]\), a zatim računamo heš vrednost tih heš vrednosti.
#include <iostream>
#include <vector>
using namespace std;
long long q = 257;
long long d = 256;
// 0 <= a mod n <= n - 1
long long mod(const long long a, const long long n)
{
if (a > 0) return a % n;
return (a % n + n) % n;
}
// a^b mod n
long long pow_mod(long long a, long long b, const long long n)
{
int d = 1;
a = mod(a, n);
while (b > 0) {
if (b & 1) {
d = mod(d * a, n);
}
b >>= 1;
a = mod(a * a, n);
}
return d;
}
bool check(const vector<vector<char>> &text,
const vector<vector<char>> &pattern,
int s, int l)
{
const int m = pattern.size();
for (int i = 0; i < m; i++) {
for (int j = 0; j < m; j++) {
if (text[i + s][j + l] != pattern[i][j]) {
return false;
}
}
}
return true;
}
vector<long long> hash_strips(const vector<vector<char>> &map, const int m)
{
const int n = map.size();
vector<long long> h (n, 0);
for (int j = 0; j < n; j++) {
for (int i = 0; i < m; i++) {
h[j] = mod(mod(d * h[j], q) + map[i][j], q);
}
}
return h;
}
long long hash_value(const vector<long long> hash, const int m)
{
long long val = 0;
for (int j = 0; j < m; j++) {
val = mod(d * val + hash[j], q);
}
return val;
}
bool rabin_karp(const vector<vector<char>> &text,
const vector<vector<char>> &pattern)
{
const long long n = text.size();
const long long m = pattern.size();
const long long h = pow_mod(d, m - 1, q);
auto t_hash = hash_strips(text, m);
auto p_hash = hash_strips(pattern, m);
long long p_val = hash_value(p_hash, m);
for (int s = 0; s < n - m + 1; s++) {
long long t_val = hash_value(t_hash, m);
for (int l = 0; l < n - m + 1; l++) {
if (p_val == t_val && check(text, pattern, s, l)) {
return true;
}
if (l < n - m) { // horizontal roll
t_val = mod(d * (t_val - h * t_hash[l]) + t_hash[l + m], q);
}
}
if (s < n - m) { // vertical roll
for (int j = 0; j < n; j++) {
t_hash[j] = mod(d * (t_hash[j] - h * text[s][j]) + text[s + m][j], q);
}
}
}
return false;
}
int main(void)
{
int n, m;
cin >> n >> m;
vector<vector<char>> text(n, vector<char> (n));
vector<vector<char>> pattern(m, vector<char> (m));
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
cin >> text[i][j];
}
}
for (int i = 0; i < m; i++) {
for (int j = 0; j < m; j++) {
cin >> pattern[i][j];
}
}
if (rabin_karp(text, pattern)) {
cout << "da" << endl;
} else {
cout << "ne" << endl;
}
return 0;
}