Torta

Jovana zna da će joj na rođendan doći ili \(m\) ili \(n\) osoba. Želi da iseče rođendansku tortu na što manji broj parčića (ne obavezno iste veličine) tako da se kombinovanjem tih parčića u oba slučaja može postići da svaki gost dobije istu količinu torte. Koji je najmanji broj potrebnih parčića?

Opis ulaza

Sa standardnog ulaza se unose brojevi \(m\) i \(n\) (manji od \(10^9\)), svaki u posebnom redu.

Opis izlaza

Na standardni izlaz ispisati najanji broj potrebnih parčića.

Primer

Ulaz

2
3

Izlaz

4

Objašnjenje

Jovana može da iseče tortu na dva parčeta veličine \(\frac{1}{3}\) i dva parčeta veličine \(\frac{1}{6}\). U slučaju da dođu dve osobe, svaka će dobiti \(\frac{1}{6}+\frac{1}{3} = \frac{1}{2}\). U slučaju da dođu tri osobe, prve dve će uzeti parčiće od \(\frac{1}{3}\), a treća dva parčeta dimenzije \(\frac{1}{6}\).

Rešenje

Zamislimo tortu kružnog oblika kao sat. Ako tortu sečemo za \(m\) osoba krenuvši prvi rez od 12 sati, rez ćemo praviti na svakih \(\frac{360^\circ}{m}\). Ako tortu sečemo za \(n\) osoba krenuvši prvi rez od 12 sati, rez ćemo praviti na svakih \(\frac{360^\circ}{n}\). Prvi rez, napravljen na 12 sati će se siguro poklopiti, a možda će biti poklapanja i nekih drugih rezova. Broj rezova koji će se poklopiti je \(\mathit{nzd}(m, n)\).

Zaista, rez se poklapa ako važi \(i \cdot \frac{360^\circ}{m} = j \cdot \frac{360^\circ}{n}\), neke \(0 \leq i < m\) i \(0 \leq j < n\). Tada je \(n\cdot i = m \cdot j\). Ako je \(p = \mathit{nzd}(m, n)\), tada je \(m = p\cdot m'\) i \(n = p\cdot n'\), za neke uzajamno proste vrednosti \(m'\) i \(n'\) i važi da je \(n' \cdot i = m' \cdot j\). Pošto su brojevi \(m'\) i \(n'\) uzajamno prosti, mora da važi da je \(j = n'\cdot j'\) i \(i = m'\cdot i'\) za neke \(i'\) i \(j'\). Dakle, \(m' \cdot n' \cdot j' = n' \cdot m'\cdot i'\), pa je \(i' = j'\). Pitanje je koliko ima takvih vrednosti koje zadovoljavaju uslove zadatka. Iz \(0 \leq i < m\), uvrštavanjem vrednosti \(i = m'\cdot i'\) i \(m = p\cdot m'\), sledi \(0 \leq m'\cdot i' < m' \cdot p\) tj. \(0 \leq i' < p\). Analogno, na osnovu \(0 \leq j < n\), važi i \(0\leq j' < p\). Dakle, svaka vrednost \(i'=j'\) od \(0\) do \(p-1\) daje neki par \((i, j)\) koji daju zajednički rez. Takvih vrednosti ima tačno \(p\).

Ukupan broj različitih rezova je dakle \(m+n-\mathit{nzd}(m, n)\), što je ujedno i broj isečenih parčića.

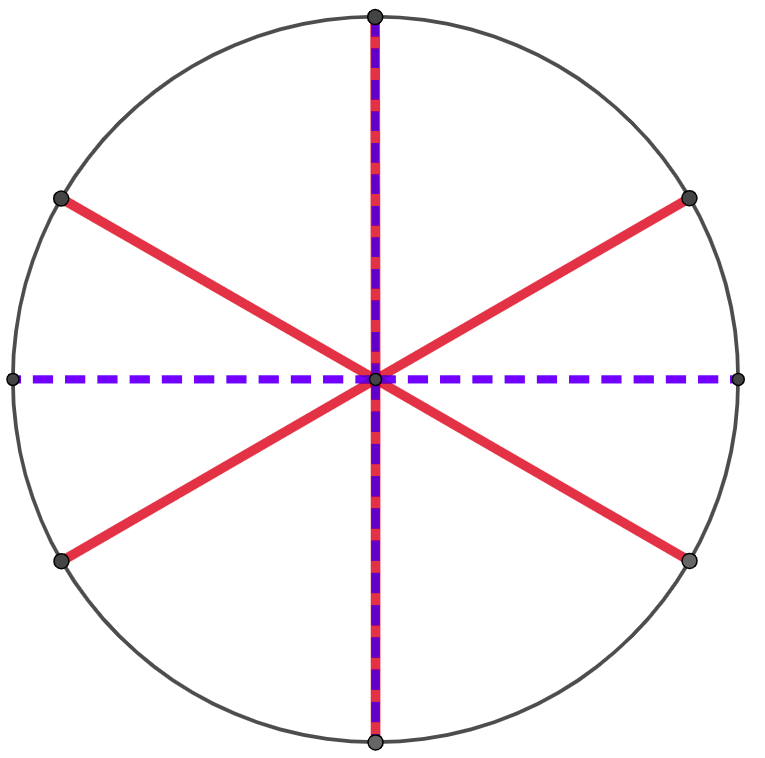
Na slici je prikazano sečenje torte na 6 i na 4 parčeta. Primećuje se poklapanje 2 reza. Ukupan broj parčića je \(6+4-2 = 8\).

Sečenje torte na 6 delova i na 4 dela 
#include <iostream>

using namespace std;

int nzd(int a, int b) {
  if (b == 0)
    return a;
  return nzd(b, a % b);
}

int main() {
  int m, n;
  cin >> m >> n;
  cout << m + n - nzd(m, n) << endl;
  return 0;
}