Bilijarski sto je pravougaonog oblika dimenzije \(m\times n\) i ima četiri rupe u ćoškovima. Posmatrajmo crtež stola, takav da mu je širina \(m\), a visina \(n\). Loptica se udara iz donjeg levog ugla (polja sa koordinatama \((0, 0)\)) duž linije koja je pod uglom od 45 stepeni u odnosu na ivice stola. Ako pretpostavimo da loptica ne usporava svoje kretanje, da se od svake se ivice odbija pod uglom od \(45^\circ\), da je veoma mala i da u rupu upada samo ako su joj koordinate centra jednake koordinati rupe, napiši program koji određuje u koju rupu će posle nekog vremena upasti, kao i koliko će se puta pre toga odbiti o ivice stola.
Sa standardnog ulaza se unose dva cela broja \(m\) i \(n\) (\(1 \leq m, n \leq 10^9\)) koji predstavljaju dimenzije stola.
Na standradni izlaz u prvom redu ispisati koordinate rupe u koju će loptica upasti, a u drugom broj odbijanja o ivice stola pre nego što se to desi.
4 3
4 0 5
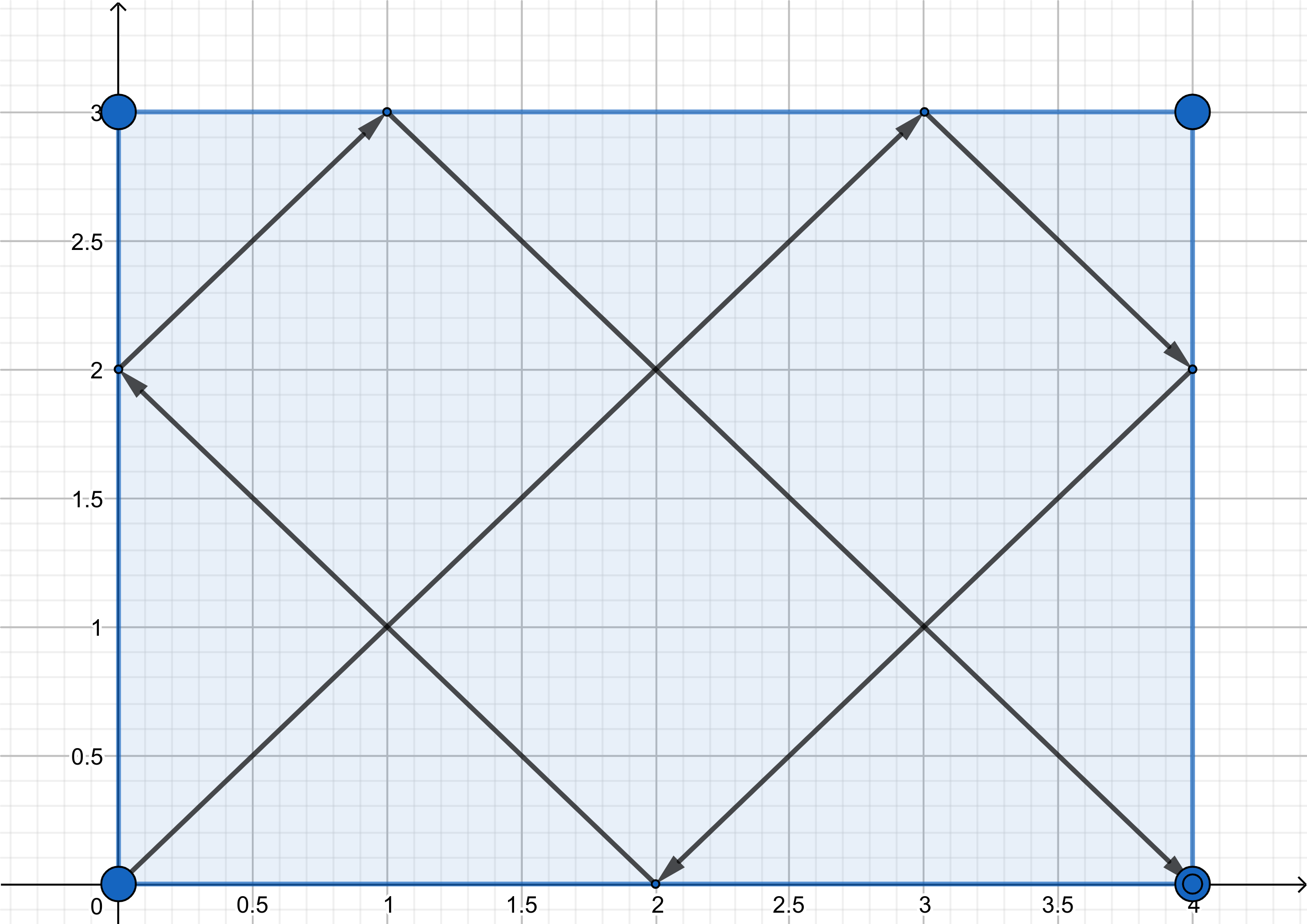
Kretanje loptice je prikazano na slici.

Da bi se loptica našla u nekoj rupi ona krećući se horizontalno treba da pređe rastojanje (dužinu pređenog puta) koje predstavlja neki umnožak širine stola i krećući se vertikalno treba da pređe rastojanje koje predstavlja neki umnožak visine stola. Pošto je intenzitet njene brzine i u horizontalnom i u vertikalnom pravcu isti (jer se stalno kreće pod uglom od 45 stepeni u odnosu na neku ivicu stola), rastojanje pređeno u horizontalnom i u vertikalnom smeru je uvek isto. Dakle, loptica upada u rupu u trenutku kada je pređeno rastojanje prvi put neki umnožak brojeva \(m\) i \(n\). Najmanji broj koji je deljiv i sa \(m\) i sa \(n\) je njihov najmanji zajednički sadržalac \(nzs(m, n)\).
Broj puta \(n_x\) koji je loptica horizontalno prebrisala celu širinu stola jednak je količniku \(nzs(m, n)\) i broja \(m\), a broj \(n_y\) puta koji je loptica vertikalno prebrisala celu visinu stola jednak je količniku \(nzs(m, n)\) i broja \(n\). Ako je broj \(n_x\) neparan, loptica se nalazi u nekoj rupi na desnoj, a ako je paran, nalazi se u nekoj rupi na levoj ivici stola, pa \(x\) koordinatu rupe lako određujemo analizom parnosti broja \(n_x\). Analogno, analizom parnosti broja \(n_y\) određujemo koordinatu \(y\) rupe.
Ako je loptica horizontalnu širinu prešla \(n_x\) puta, ona se o neku levu i desnu ivicu odbila tačno \(n_x - 1\) puta. Slično, ako je vertikalnu širinu prešla \(n_y\) puta, o gornju i donju ivicu se odbila tačno \(n_y - 1\) puta. Ukupan broj odbijanja je, dakle, \((n_x - 1) + (n_y - 1)\).
NZS dva broja možemo izračunati Euklidovim algoritmom, ali moramo voditi računa da zbog velikih ulaznih parametara može nastupiti prekoračenje i moramo koristiti adekvatne tipove podatka.
#include <iostream>
using namespace std;
int nzd(int a, int b)
{
while (b > 0) {
int ost = a % b;
a = b;
b = ost;
}
return a;
}
long long nzs(int a, int b)
{
return ((long long) a / nzd(a, b)) * b;
}
int main()
{
int m, n;
cin >> m >> n;
long long S = nzs(m, n);
int nx = S / m, ny = S / n;
int x = nx % 2 == 0 ? 0 : m;
int y = ny % 2 == 0 ? 0 : n;
cout << x << " " << y << endl;
cout << (nx - 1) + (ny - 1) << endl;
return 0;
}Računanje NZS možemo izbeći. Za rešenje nama je potrebno da znamo vrednosti \(n_x = nzs(m, n) / m\) i \(n_y = nzs(m, n) / n\). Pošto je \(nzs(m, n) = (mn) / nzd(m, m)\), važi da je \(n_x = n / nzd(m, n)\) dok je \(n_y = m / nzd(m, n)\). Time izbegavamo potrebu za radom sa velikim brojevima i izbegavamo mogućnost nastanka prekoračenja.
#include <iostream>
using namespace std;
int nzd(int a, int b)
{
while (b > 0) {
int r = a % b;
a = b;
b = r;
}
return a;
}
int main()
{
int m, n;
cin >> m >> n;
int N = nzd(m, n);
int nx = n / N, ny = m / N;
int x = nx % 2 == 0 ? 0 : m;
int y = ny % 2 == 0 ? 0 : n;
cout << x << " " << y << endl;
cout << (nx - 1) + (ny - 1) << endl;
return 0;
}