Opis glavnog rešenja
Naivno zadatak možemo rešiti tako što za svaki raspon dužine \(k\) računamo medijanu tog raspona. Naivno računanje medijane zahteva sortiranje, dok za bolje rešenje možemo iskoristiti QuickSelect algoritam.
Zadatak se može bolje rešiti na više načina, ali kako znamo da je \(t_i \in (0, 100)\), pogodno je iskoristiti Fenvikova drveta. Ideja algoritma se zasniva na tehnici pokretnog prozora raspona \(k\). Inicijalno, prozor obuhvata prvih \(k\) temperatura. U svakom koraku \(i = 0, \ldots, n - k - 1\) u prozor se dodaje temperatura \(t_{i + k}\) i iz prozora se izbacuje temperatura \(t_i\). Dodatno u svakom koraku \(i = 0, \ldots, n - k\) se računa i ispisuje medijana trenutnog prozora. Razmotrimo, dalje, detalje algoritma.
Neka je \(f\) niz dužine \(N = 100\) (jer \(t_i \in (0, 100)\)), u kome će se održavati broj pojavljivanja temperatura određene vrednosti koje upadaju u prozoru dužine \(k\). Npr. ukoliko se, trenutno, u prozoru nalazi \(5\) temperatura čija je vrednost \(23\), onda \(f_{23} = 5\). Zbog toga, trenutno stanje niza \(f\) predstavlja trenutno stanje prozora. Inicijalno, niz \(f\) sadrži nule. Za prvih \(k\) temperatura, ažuriramo niz \(f\) tako što \(f_{t_i}\) uvećamo za jedan za svako \(i = 0, \ldots, k - 1\). Dalje, u svakom koraku \(i = 0, \ldots, n - k - 1\) ažuriramo niz \(f\) tako što \(f_{t_i}\) smanjimo za jedan i \(f_{t_{i + k}}\) uvećamo za jedan. Pri tome, treba iskoristiti \(f\) i izračunati medijanu u svakom koraku \(i = 0, \ldots, n - k\). Niz \(f\) nam omogućava da medijanu izračunamo binarnom pretragom, tj. tražimo poziciju \(p\) čija će prefiksna suma biti donja granica za \(\lceil k / 2 \rceil\). Preciznije, kriterijum binarne pretrage je:
\[\left(\sum_{t = 1}^p f_t\right) \geq \lceil k/2 \rceil \land \left(\sum_{j = 1}^{p-1} f_j\right) < \lceil k / 2 \rceil.\]
Kako kriterijum binarne pretrage uključuje računanje prefiksnih suma, radi bolje efikasnosti, zgodno je da je \(f\) bude implementirano preko Fenvikovog stabla. Tada će ukupna složenost algoritma biti \(O(k \log N + (n - k + 1) \log^2 N)\). Ovu složenost možemo, dalje, smanjiti na \(O(n \log N)\) korišćenjem specijalizovane pretrage donje granice za Fenvikovo stablo. U daljem tekstu će biti opisana ta procedura.
Želimo da nađemo poziciju \(p\) čija će prefiksna suma biti donja granica za neku vrednost \(v\). Zbog strukture Fenvikovog stabla, dovoljno je razmatrati pozicije koje su stepen dvojke. Inicijalno, poziciju \(p\) i trenutnu prefiksnu sumu \(s\) postavimo na nulu. U svakom koraku \(i = \lfloor \log N \rfloor, \ldots, 0\), posmatraćemo poziciju \(p + 2^i\). Ukoliko je pozicija validna, tj. \(p + 2^i < N\), razmatramo da je moguće bolje oceniti donju granicu. Preciznije, ako je \(s + f_{p + 2^i} < v\), onda \(s \gets s + f_{p + 2^i}\) i \(p \gets p + 2^i\).
Za bolje razumevanje razmotrimo jedan primer: Neka je dat niz \(a = \langle 1, 0, 2, 1, 1, 3, 0, 4, 2, 5, 2, 2, 3, 1, 0, 2 \rangle\). Pretpostavimo da je tražena vrednost \(v=27\). Na sledećoj slici je prikazano Fenvikovo stablo za niz \(a\), zajedno sa procedurom pretrage.
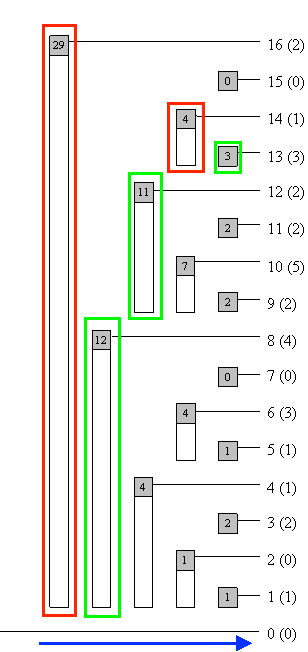
Plava strelica prikazuje smer u kome se pretraga obavlja. Crvenom su prikazane pozicije u kojima nije moguće bolje oceniti donju granicu, dok su zelenom prikazane pozicije u kojima je ažurirana donja granica.
U sledećoj tabeli je prikazan postupak algoritma kroz dati primer.
| \(i\) | \(p\) | \(s\) | \(f_{p + 2^i}\) | \(s + f_{p + 2^i}\) | \(s + f_{p + 2^i} < v\) |
|---|---|---|---|---|---|
| 0 | 0 | ||||
| 4 | 0 | 0 | 29 | 29 | ne |
| 3 | 0 | 0 | 12 | 12 | da |
| 2 | 8 | 12 | 11 | 23 | da |
| 1 | 12 | 23 | 4 | 27 | ne |
| 0 | 12 | 23 | 3 | 26 | da |
| 13 | 26 |
#include <iostream>
#include <vector>
#include <cmath>
using namespace std;
int BIT_sum(const vector<int> &bit, int k)
{
int sum = 0;
while (k > 0) {
sum += bit[k];
k -= k & -k; // k = f(k)
}
return sum;
}
void BIT_update(vector<int> &bit, int k, const int x)
{
while (k <= bit.size()) {
bit[k] += x;
k += k & -k;
}
}
// O(log^2 n)
int BIT_binary_search(const vector<int> &bit, int val)
{
int l = 1, r = bit.size();
while (l != r) {
int m = (l + r) / 2;
if (BIT_sum(bit, m) < val) {
l = m + 1;
} else {
r = m;
}
}
return l;
}
// O(log n)
int BIT_search(const vector<int> &bit, const int val)
{
int sum = 0, pos = 0;
for (int i = log2(bit.size()); i >= 0; i--) {
if (pos + (1 << i) < bit.size() && sum + bit[pos + (1 << i)] < val) {
sum += bit[pos + (1 << i)];
pos += (1 << i);
}
}
return pos + 1;
}
int main(void)
{
int n, k; cin >> n >> k;
vector<int> t(n);
for (int i = 0; i < n; i++) {
cin >> t[i];
}
vector<int> f(100);
for (int i = 0; i < k; i++) {
BIT_update(f, t[i], 1);
}
for (int i = 0; i < n - k + 1; i++) {
double median = 0;
if (k % 2 == 1) {
median = BIT_search(f, (k + 1) / 2);
} else {
median = (BIT_search(f, k / 2) + BIT_search(f, k / 2 + 1)) / 2;
}
cout << median << endl;
if (i < n - k) {
BIT_update(f, t[i], -1);
BIT_update(f, t[i + k], 1);
}
}
return 0;
}