Osvoji region

Data je binarna matrica \(\mathbf{M}_{n \times m} = (m_{ij})\) na kojoj je prikazana teritorija plavog i crvenog tima. Ukoliko je element \(m_{ij}\)

Ukoliko je neki region koji okupira plavi tim u potpunosti okružen poljima crvenog tima, onda taj region biva osvojen i njegova polja dodeljujemo crvenom timu. Drugim rečima, ukoliko region koji okupira plavi tim nema izlaz van granica matrice, onda on postaje crven.

Potrebno je promeniti i ispisati novu podelu teritorije.

Napomena: Povezanost polja posmatramo samo u četiri pravca (gore, dole, levo, i desno).

Opis ulaza

Sa standardnog ulaza se učitava dimenzija matrice \(n\) i \(m\), a nakon toga i elementi matrice \(\mathbf{M}_{n \times m}\).

Opis izlaza

Na standardni izlaz ispisati stanje matrice \(\mathbf{M}_{n \times m}\) nakon što crveni tim osvoji sve moguće regione.

Primer

Ulaz

5 5
0 1 1 1 0
1 0 0 1 0
1 0 1 1 1
1 1 1 0 1
0 0 0 1 1

Izlaz

0 1 1 1 0
1 1 1 1 0
1 1 1 1 1
1 1 1 1 1
0 0 0 1 1

Rešenje

Opis glavnog rešenja

Zadatak možemo rešiti primenom tehnike pretrage u dubinu ili širinu. Ali prikažimo i još jedan način korišćenjem strukture disjunktnih skupova. Ideja algoritma je da grupišemo regione nula u disjunktne skupove i da sve one regione nula koji su ograničeni jedinicama pretvorimo u jedinice. Razradimo sada algoritam detaljnije.

Na početku algoritma, svaki element matrice postaje jedinični skup. Pri tome, dodajemo još jedan jedinični skup koji će sadržati dummy element. Prolaskom kroz matricu za svaku poziciju \((i, j)\) proverimo da li se na njoj nalazi nula. Ukoliko je to slučaj, proveravamo da li je pozicija \((i, j)\) pripada prvoj ili poslednjoj koloni, odnosno prvoj ili poslednjoj vrsti. Ukoliko pozicija \((i, j)\) pripada prvoj ili poslednjoj koloni, odnosno prvoj ili poslednjoj vrsti, onda vršimo uniju skupa kome pripada element na poziciji \((i, j)\) sa skupom kome pripada dummy element. Inače, vršimo uniju skupa kome pripada element na poziciji \((i, j)\) sa skupovima kojima pripadaju elementi na pozicijama \((i-1, j)\), \((i+1, j)\), \((i, j-1)\), i \((i, j+1)\) samo ako se na njima nalazi nula i ne pripadaju prvoj ili poslednjoj koloni, odnosno prvoj ili poslednjoj vrsti.

Na kraju ovog postupka, regioni nula koji su ograničeni jedinicama postaju zasebni disjunktni skupovi, dok će regioni nula koji nisu ograničenima jedinicama pripadati skupu kome pripada i dummy element. Na slici, ispod, prikazani su različitim bojama disjunktni skupovi, dobijeni ovim postupkom, za dati primer. Naravno, svaka jedinica ostaje u svom jediničnom skupu.

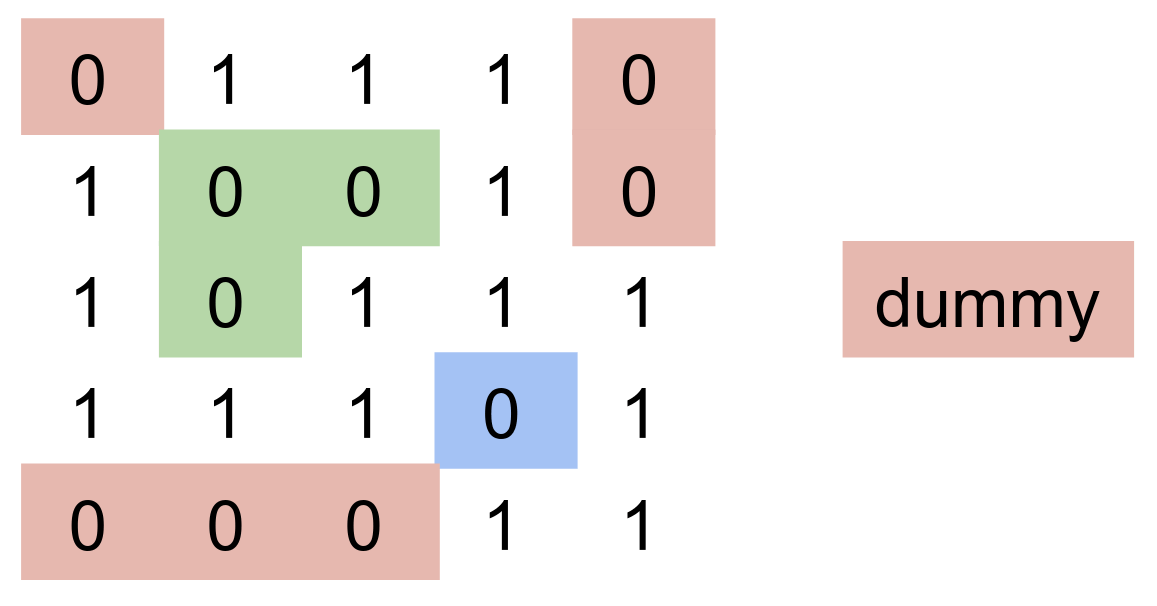
Potrebno je još proći kroz elemente matrice, i sve nule koje nisu u istom skupu, kao i dummy element, prepisati jedinicom.

Složenost inicijalizacije \(n \cdot m + 1\) disjunktnih podskupova je \(O(n \cdot m)\). Ako pretpostavimo da je složenost unije i pronalaska predstavnika skupa konstantne složenosti i kako se za svaku poziciju \((i, j)\) može izvršiti najviše \(4\) operacije unije, onda je složenost postupka unije svih pozicija \(O(n \cdot m)\). Složenost zamene regiona nula sa jedinicama je, takođe, \(O(n \cdot m)\), kako za svaku poziciju \((i, j)\) izvršavamo najviše \(2\) operacije pronalaska predstavnika skupa. Ukupna složenost algoritma je \(O(n \cdot m)\).

#include <iostream>
#include <string>
#include <vector>

using namespace std;

vector<int> parent;
vector<int> rang;

void UF_init(int n) 
{
    parent.resize(n);
    rang.resize(n);

    for (int i = 0; i < n; i++) {
        parent[i] = i;
        rang[i] = 0;
    }
}

int UF_find(int x) 
{
    while (x != parent[x]) {
        parent[x] = parent[parent[x]];
        x = parent[x];
    }

    return x;
}

void UF_union(int x, int y) 
{
    int fx = UF_find(x);
    int fy = UF_find(y);

    if (fx == fy) return;

    if (rang[fx] < rang[fy]) {
        parent[fx] = fy;
    } else if (rang[fy] < rang[fx]) {
        parent[fy] = fx;
    } else {
        parent[fx] = fy;
        rang[fy]++;
    }
}

int code(int i, int j, int m)
{
    return i * m + j;
}

int main() 
{
    int n, m; cin >> n >> m;

    vector<vector<int>> board(n, vector<int>(m));
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < m; j++) {
            cin >> board[i][j];
        }
    }

    UF_init(n * m + 1);

    const int dummy = n * m;

    for (int i = 0; i < n; i++) {
        for (int j = 0; j < m; j++) {
            if (board[i][j] == 0) {
                if (i == 0 || j == 0 || i == n - 1 || j == m - 1) {
                    UF_union(dummy, code(i, j, m));
                } else {
                    if (i > 0 && board[i - 1][j] == 0) {
                        UF_union(code(i, j, m), code(i - 1, j, m));
                    }
                    if (i < n - 1 && board[i + 1][j] == 0) {
                        UF_union(code(i, j, m), code(i + 1, j, m));
                    }
                    if (j > 0 && board[i][j - 1] == 0) {
                        UF_union(code(i, j, m), code(i, j - 1, m));
                    }
                    if (j < m - 1 && board[i][j + 1] == 0) {
                        UF_union(code(i, j, m), code(i, j + 1, m));
                    }
                }
            }
        }
    }

    for (int i = 0; i < n; i++) {
        for (int j = 0; j < m; j++) {
            if (board[i][j] == 0 && UF_find(dummy) != UF_find(code(i, j, m))) {
                board[i][j] = 1;
            }
        }
    }

    for (int i = 0; i < n; i++) {
        for (int j = 0; j < m; j++) {
            cout << board[i][j] << " ";
        }
        cout << endl;
    }

    return 0;
}