Postavka problema

U ravni je dat skup paralelnih pravih, pri čemu je rastojanje između bilo koje dve susedne prave d (d > 0). Na ravan se baca igla dužine l (l < d). Potrebno je odrediti verovatnoću da igla seče neku od pravih.

Model problema

Modelovonje problema podelićemo u pet koraka:

     1.  Prepoznavanje slučajnih veličina koje su nam od interesa.

     2.  Definisanje prostora svih ishoda za prethodno uočene slučajne veličine.

     3.  Definisanje prostora povoljnih ishoda (ishodi u kojima se eksperiment realizovao).

     4.  Određivanje zajedničke raspodele verovatnoća na prethodno definisanom prostoru ishoda.

     5.  Rešavanje problema u prethodno postavljenim okvirima.

1. Slučajne veličine. Bilo koji ishod eksperimenta je u potpunosti određen položajem igle u ravni. Zbog početnog uslova (l < d) igla ne može da seče više od jedne prave, pa je dovoljno posmatrati položaj u odnosu na najbližu pravu. U odnosu na ovu pravu položaj igle je u potpunosti odeređen dvema slučajnim veličinama:
   
   X - ugao igle u odnosu na pravu meren u smeru suprotnom od smera kretanja kazaljke na satu
   
   Y - rastojanje središta igle od prave Za slučajne veličine definisane na ovaj način važi: 0 ≤ X ≤ π, 0 ≤ Y ≤ d/2.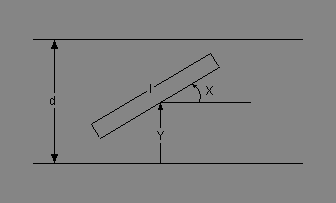
   
   
   
   
2. Prostor svih ishoda. Prostor svih ishoda (X,Y) odgovara pravougaoniku:
   
   ∏ = (X,Y) = {(x, y): 0 ≤ x ≤ π , 0 ≤ y ≤ d/2}
   
   
   
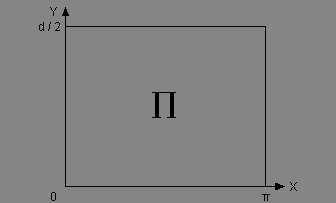
   gde x, y predstavljaju realizovane vrednosti slučajnih veličina X i Y, respektivno.
   
   
   
   
3. Prostor povoljnih ishoda. Da bi odredili prostor povoljnih ishoda moramo da prepoznamo one tačke prostora svih ishoda u kojima igla seče neku od pravih (tačke u kojima se eksperiment realizovao). Neformalno, igla seče pravu ukoliko je rastojanje središta igle od te prave dovoljno malo za neku fiksiranu ugaonu poziciju igle. Što znači da ako koordinatu donjeg kraja igle napišemo u obliku y - (l/2)sin(x), zaklučujemo da se presek javlja ukoliko je ova vrednost negativna, tj. ako važi:
   
   y ≤ (l/2)sin(x)
   
   
   
   
   
   
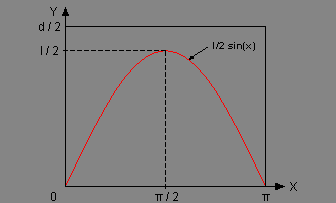
4. Zajednička raspodela verovatnoća. Zajednička raspodela verovatnoća slučajnih veličina X i Y je određena njihovom zajedničkom funkcijom gustine f_(X,Y)(x,y). Da bi odredili zajedničku gutinu moramo prvo utvrditi način na koji se eksperiment izvodi. Kako se igla baca na slučajan način, možemo uzeti da je raspodela slučajne veličine X uniformna na intervalu [0,π], tako da je njena marginalna gustina raspodele verovatnoća:
   
   f_X(x) = 1 / π     0 ≤ x ≤ π
   
   Analogno, možemo smatrati da slučajna veličina Y ima uniformnu raspodelu na intervalu [0,d/2], tako da je njena marginalna gustina raspodele verovatnoća data na sledeći način:
   
   
   f_Y(y) = 2 / d     0 ≤ y ≤ d/2
   
   Uočimo da poznavanje ugaone pozicije igle ne može da utiče na njeno rastojanje od prave i obratno. Stoga, slučajne veličine X i Y možemo smatrati nezavisnim, pa je njihova zajednička funkcija gustine raspodele verovatnoća jednaka proizvodu njima odgovarajućih marginalnih:
   
   
   f_(X,Y)(x,y) = 2 / πd      0 ≤ x ≤ π      0 ≤ y ≤ d/2
   
   
   
   
5. Rešavanje problema. Da bi odredili verovatnoću preseka igle sa nekom od pravih moramo da integralimo prethodno utvrđenu zajedničku gustinu na prostoru povoljnih ishoda:
   
   
   

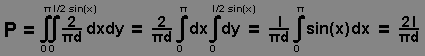
Posledica

Bifonov eksperiment nam daje mogućnost procene broja π. Naime, ako se igla baca veliki broj puta (n) na ravan podeljenu paralelnim pravama i ako m puta preseče neku pravu, tada se, prema statističkoj definiciji verovatnoće (posledica zakona velikih brojeva koji kaže da relativna frekvencija nekog događaja u eksperimentu koji se ponavlja, konvergira skoro svuda ka stvarnoj vrednosti verovatnoće tog događaja), može uzeti da je verovatnoća preseka igle sa nekom pravom približno jednaka m/n. Tako da na osnovu prethodno dobijenog rezultata koji daje tačnu vrednost ove verovatnoće zaključujemo da važi:

Zaključak

Bifonov eksperiment nije efikasan metod aproksimacije broja π. Za procenu broja π na četiri decimale potrebno je oko 100 miliona bacanja.