ALGORITMI ZA FORMIRANJE KONVEKSNOG OMOTAČA U 2D

Uvod

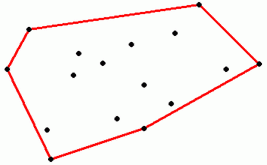
2D-konveksni omotač skupa tačaka definišemo kao najmanji konveksni poligon koji obuhvata sve tačke. "Najmanji" se odnosi kako na površinu, tako i na obim poligona.

Algoritam za konveksni omotač korisiti se u robotici, obradi digitalnih slika i prepoznavanju oblika, ali je značajanu primenu našao kao neophodni deo drugih algoritama, kao što su:

određivanje da li tačka leži "između" skupa drugih tačaka
određivanje da li se dva skupa tačaka "preklapaju"
nalaženje najmanjeg pravougaonika koji obuhvata skup tačaka
određivanje "grubog" oblika definisanog skupom tačaka

Algoritmi za nalaženje konveksnog omotača

Naziv algoritma	Opis/komentari	Vremenska složenost
Ivične/Unutrašnje tačke	Tačke su ivične akko se nalaze izvan svakog trougla definisanog sa bilo koje druge tri tačke tog skupa. (Moramo uporediti sve tačke (O(n)) sa svim mogućim trouglovima (O(n³)))	O(n⁴)
Ivične duži (spori algoritam)	Duž se nalazi u konveksnom omotaču kada sve tačke leže na ili sa iste strane prave definisane dvema tačkama iz skupa. (Moramo uporediti sve tačke (O(n)) sa svim mogućim pravama određenim parovima tačaka (O(n²)))	O(n³)
Pakovanje poklona	Počinje od ivične tačke i linija se "uvija" oko skupa tačaka. (Algoritam je takođe poznat pod nazivom Jarvis March algoritam)	O(n²) ili O(nh) (h = ivice omotača)
Brzi	Pomalo podseća na quicksort algoritam.	prosečno O(n log n) najgori slučaj O(n²)
Graham-ov algoritam	Optimalne kompleksnosti.	O(n log n)

Ivične/Unutrašnje tačke

Ideja

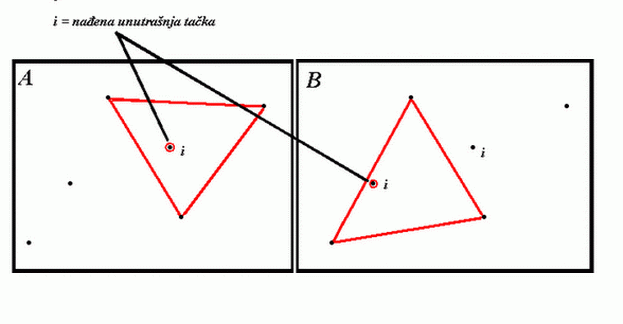
Tačke su unutrašnje ako i samo ako su unutar svakog trougla određenog bilo kojim trima drugim tačkama tog skupa. Na sledećoj slici prikazan je razulat takva dva testa. U koracima A i B identifikovane su dve različite unutrašnje tačke.

Kada pronađemo sve unutrašnje tačke konveksni omotač se kontstruiše na osnovu skupa ivičnih tačaka.

Vremenska složenost

Opšti slučaj: Moramo uporediti sve tačke (O(n)) sa svim mogućim trouglovima (O(n³)), pa je algoritam složenosti O(n⁴).
Najgori slučaj: Nema specijalnih slučajeva. Algoritam je uvek složenosti O(n⁴) jer postoje četiri for ciklusa.
Najbolji slučaj: Nema specijalnih slučajeva. Algoritam je uvek složenosti O(n⁴) .

Pseudokod

for each i do
    for each j != i do
        for each k != i != j do
            for each l != i != j != k do
                if p(l) je levo ili na ( p(i),p(j) ) i
                                      ( p(j),p(k) ) i
                                      ( p(k),p(l) )
                then p(i) nije ivična/ekstremna
Konstruisati omotač od ivičnih tačaka

...povratak

Ivične duži (spori algoritam)

Ideja

Duž je ivična ako sve tačke leže na ili sa iste strane prave određene dvema tačkama tog skupa. Sledeća slika prikazuje dva takva testa. U prvom slučaju (slika A), duž je ivična jer su sve tačke skupa sa njene leve strane. Na slici B je suprotan slučaj - tačke se nalaze sa obe strane linije, pa duž nije u omotaču.

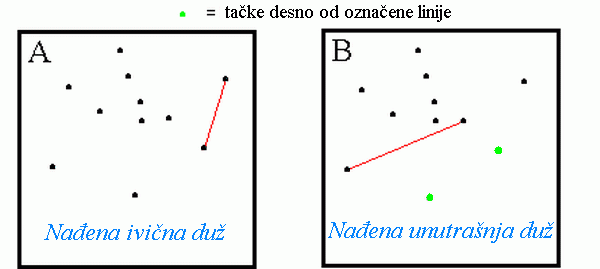
Nakon što se obradi svaka linija, nađene su sve ivice i konveksni omotač može biti konstruisan.

Vremenska složenost

Opšti slučaj: Moramo uporediti sve tačke (O(n)) sa svim mogućim linijama određenim parovima tačaka skupa (O(n²)), pa je algoritam složenosti O(n³).
Najgori slučaj: Nema specijalnih slučajeva. Algoritam je uvek složenosti O(n³).
Najbolji slučaj: Nema specijalnih slučajeva. Algoritam je uvek složenosti O(n³).

Pseudokod

for each i do
    for each j != i do
        for each k != i != j
            if p(k) nije levo ili na ( p(i), p(j) )
                then ( p(i), p(j) ) nije ekstremna
Konstruisati omotač od ekstremnih ivica

...povratak

Pakovanje poklona ili Jarvis March algoritam

Ideja

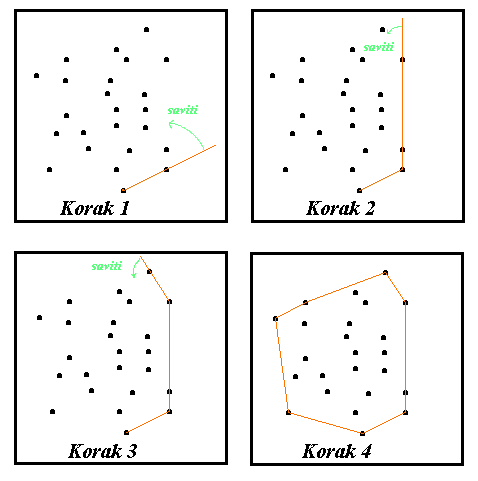
Algoritam počinje od najniže (krajnje desne) tačke, a zatim nalazi tačku koja zaklapa najmanji ugao (u odnosu na x-osu) sa ovom tačkom. Ivica omotača mora da spaja ove dve tačke (korak 1). Dalje, nalazimo tačku koja zaklapa najmanji ugao sa ovom formiranom ivicom. U stvari, linija kojoj pripada ivica omotača se "savija" u smeru suprotnom od kretanja kazaljke na satu sve dok ne obuhvati drugu tačku. Ako su nađene dve tačke koje imaju isti ugao, tada se uzima tačka koja je najudaljenija od pivot tačke (korak 2). Proces "pakovanja" linije oko skupa tačaka se nastavlja (korak 3) dok se ne dođe do početne tačke (korak 4) i tada je konveksni omotač formiran.

Vremenska složenost

Opšti slučaj: Očigledno je da je za svaku otkrivenu tačka ivice omotača (O(n) ili preciznije O(h), gde je h broj tačaka omotača) treba naći sledeću tačku omotača. Ovo se postiže upoređivanjem sa svakom tačkom, pa je ukupna vremenska složenost O(n²), ili tačnije O(nh).
Najgori slučaj: Kada su sve tačke na konveksnom omotaču i nema kolinearnih tačaka, složenost algoritma je O(n²).
Najbolji slučaj: Najbolji slučaj za ovaj algoritam je da ima što više tačaka u unutrašnjosti konveksnog omotača. Do ove situacije dolazi kada sve tačke leže unutar nekog trougla i tada vremenska složenost postaje O(n).

Pseudokod

Naći najnižu (krajnje desnu) tačku
Neka je i(0) indeks i stavimo i=i(0)
repeat
    for each j != i do
        Izračunati ugao u skk smeru od prethodne ivice omotača
    Neka je k = indeks tačke sa najmanjim uglom
    Output (p(i),p(k)) = ivica omotača
    i = k
until i = i(0)

...povratak

Brzi algoritam

Ideja

Izložen algoritam je verzija koju je predložio O'Rourke.

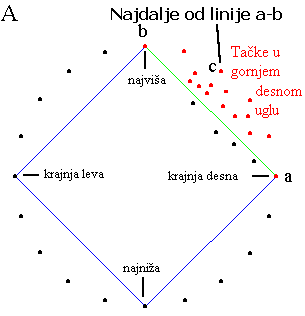
Brzi algoritam započinje generisanjem četvorougla koji spaja ivične tačke orijentisan kao kompas (slika A). Samo one tačke koje se nalaze izvan četvorougla mogu biti na omotaču i biće razmatrane u daljem računu. Svaka od četiri oblasti izvan četvorougla će biti naizmenično razmatrana i svaka će biti rekurzivno obrađivana korišćenjem QuickHull funkcije. Procedura primenjena na gornji desni ugao prikazana je na sledećoj slici.

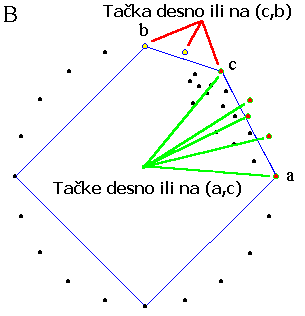
Slika A prikazuje četiri ekstremne tačke, koje formiraju ivice četvorougla, i odabir tačaka u krajnjem desnom uglu. Konačno, slika A ističe tačku c najudaljeniju od linije a-b. Sledeći korak procedure je definisanje dva skupa tačaka - one sa desne strane ili na duži (a,c) i one sa desne strane ili na duži (c,b) (slika B). Za ove skupove tačaka dva puta pozivamo funkciju QuickHull.

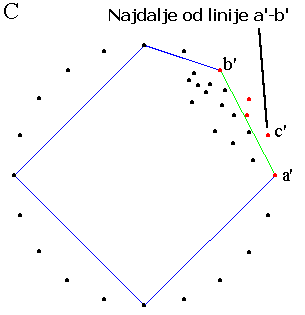
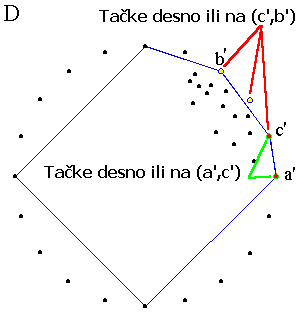
Na slici ispod prvi od novih skupova tretiramo kao u prethodnom slučaju, tj. nalazimo tačku najudaljeniju od duži (a',b') i označavamo је sa c' (slika C), a zatim razmatramo nove skupove tačaka desno ili na (a',c') i (c',b') (slika D)...

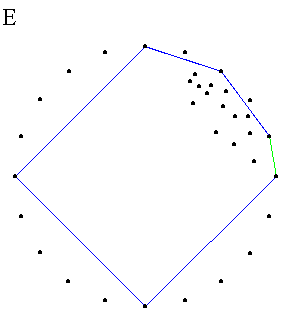
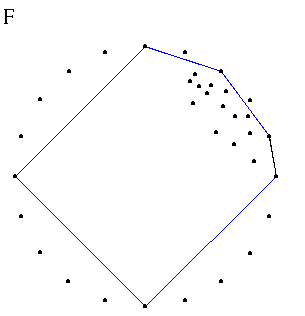
Algoritam nastavlja sa još jednim pozivom QuickHull funkcije za nova dva sukpa. Slike E i F prikazuju rezultat ovog poziva za prvi skup. U tom slučaju, samo su dve tačke u skupu i rekurzija se završava vraćajući dve tačke omotača koje čine ivicu (na slici F crna linija označava ivicu omotača).

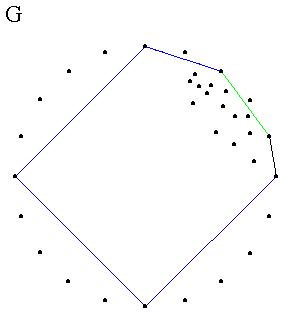
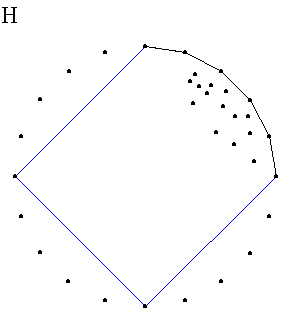
Sada razmatramo drugi skup (slika G). Primenjujemo prethodni postupak na skupove tačaka sve dok se ne izvrše sve rekurzije za gornji desni ugao i ne formira konveksni omotač za ovu oblast (slika H).

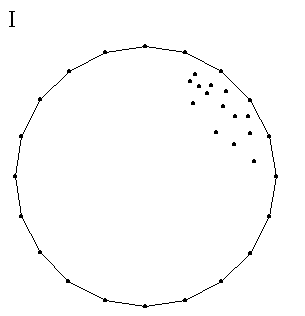
Kada primenimo prethodno izloženu proceduru na gornji levi, donji levi i donji desni ugao, formirali smo konveksni omotač
(slika I).

Vremenska složenost

Opšti slučaj: Kao u slučaju quicksort funkcije, tačke će biti podeljene u dva jednaka skupa, pa je dubina rekurzije log n. Na svakom nivou rekurzije izvršava se O(n) operacija, stoga je ukupna složenost O(n log n).
Najgori slučaj: Slično slučaju quicksort algoritma, postoje specijalni skupovi koji se ne dele na povoljan način tokom rekurzivnih poziva. Ovo dovodi do O(n) rekurzija, pa je ukupna složenost O(n²).
Najbolji slučaj: Ako se sve tačke mogu eliminisati pri identifikovanju četiri ekstremne tačke (O(n) operacija), tada je dalja obrada nepotrebna i ukupna složenost postaje O(n).

Pseudokod

Locirati krajnje levu, krajnje desnu, najnižu i najvišu tačku
Povezati te tačke u četvorougao
POzvati QuickHull za četiri trougaone oblasti izvan četvorougla
function QuickHull(a,b,S)
    if S={a,b} then return(a,b)
    else
        c = indeks tačke najdalje od (a,b)
        A = tačke desno od (a,c)
        B = tačke desno od (c,b)
        return QuickHull(a,c,A) + QuickHull(c,b,B)

Varijacije brzog algoritma

Wenger je objavio randomized QuickHull algoritam sa vremenskom složenošću O(n log h), gde je h broj tačaka u konveksnom omotaču.

...povratak

Graham-ov algoritam

Ideja

Graham je 1972. godine objavio rad u kome je predstavio relativno jednostavan algoritam za računanje konveksnog omotača konačnog skupa tačaka u ravni sa vremenskom složenošću O(n log n) u najgorem slučaju.

U nastavku je izložena verzija algoritma koju je predložio O'Rourke i koja se malo razlikuje od originalnog Graham Scan algoritma.

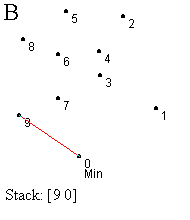
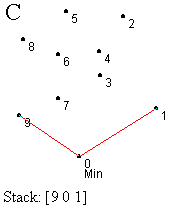
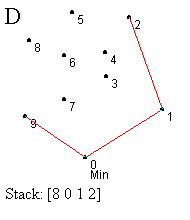
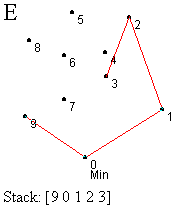
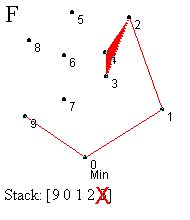
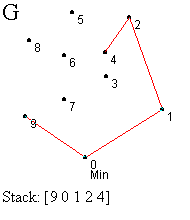
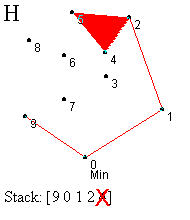
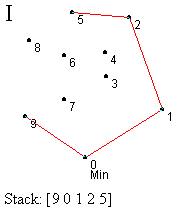
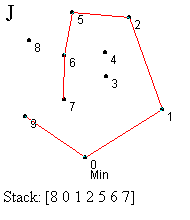
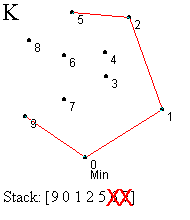
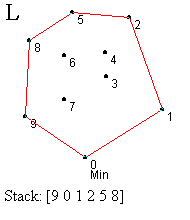
Prvi korak je identifikacija najniže (krajnje desne) tačke - označimo je sa 0. Ova tačka se mora nalaziti na omotaču (korak A). Sledeći zadatak je sortiranje svih tačaka prema uglu koji zaklapaju sa početnom tačkom, merenom u smeru suprotnom od kretanja kazaljke na satu u odnosu na x-osu (korak B). Tačka koja gradi najveći ugao se gura na stek ispred tačke 0 (korak B). Zatim redom obrađujemo tačke počev od one sa najmanjim uglom (tačka 1), dok ne dođemo do krajnje tačke (tačka 9). Ovaj proces uključuje test za strogo levo skretanje od tačke sa vrha steka ka testiranoj tački. Ako je nađeno skretanje u levo, ta tačka se gura na stek i prelazi se na obradu naredne tačke. Ako nije nađeno skretanje u levo, tada se uklanja tačka sa vrha steka i ista tačka se ponovo proverava. Ovaj proces ilustrovan je koracima C-L.

U koraku C testiramo da li je tačka 1 levo od linije određene tačkama 0 i 9. U ovom slučaju jeste, pa je guramo na stek. Slično, tačke 2 i 3 su gurnute na stek (koraci D i E). Kada testiramo tačku 4, vidimo da je ona desno od linije definisane sa 2 i 3, pa uklanjamo tačku 3 sa vrha steka (korak F). U narednom koraku nalazimo da je tačka 4 levo od tačaka 1,2 i guramo je na stek (korak G). Ipak, kada proverimo tačku 5 u odnosu na 2 i 4, otkrivamo skretanje u desno, te uklanjamo 4 sa vrha steka. Ponovnom proverom tačke 5, zaključujemo da skreće levo od tačaka 1 i 2, pa je ona novi vrh steka. Nastavljamo proces, prvo postavljajući tačku 6, a zatim i 7, na vrh steka (korak J). Naredni test pokazuje da je 8 sa desne strane obe ove tačke, pa ih uklanjamo sa steka (korak K). Daljim razmatranjem dolazimo da toga da 8 treba da bude na steku i konačno stižemo do tačke 9 i završavamo proces (korak L). Konveksni omotač je formiran.

Pseudokod

Naći najnižu (krajnje desnu) tačku
Označiti je sa p(0)
Sortirati ostale tačke prema uglu sa p(0)
    ( u grupi sa istim uglom, sortirati ih prema rastojanju od p(0) )
    Označiti ih sa p(1),...,p(n-1)
    Stack S=(p(n-1),p(0))=(p(t-1),p(i)); t = indeks vrha
    i = 1
    while i < n do
        if p(i) strogo levo od ( p(t-1),p(t) )
        then Push(S,i); i = i + 1
        else Pop(S)

Vremenska složenost

Može biti najviše n guranja i n uklanjanja sa steka, te je složenost ovog dela algoritma O(n). Složenošću dominira sortiranje, a za njega je poznata donja granica O(n log n)

Opšti slučaj: O(n log n).
Najgori slučaj: O(n log n).
Najbolji slučaj: O(n log n).

...povratak