|
|
Circle l and point H in its plane are given. Inscribe a triangle ABC in circle l such that
its orthocenter is point H, and side BC is congruent to segment a, where a is given.
|
Lemma |
|
Segment determined by center O of the circumscribed circle around a triangle ABC and the
foot of the perpendicular from point O on side BC of the triangle (point D) is congruent to
|AH|/2, where H is the orthocenter of the triangle ABC.
|
| Proof |
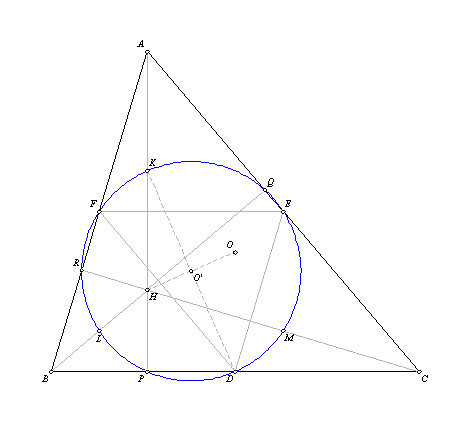
To prove the Lemma we are going to use the Euler circle of the triangle ABC. As we already
know the midpoints of the sides, the feet of the perpendiculars and midpoints of the segments which
connect the orthocenter with the vertices belong to one circle - Euler circle.
Let us denote:
a=BC, b=CA, c=AB,
ha, hb, hc - altitudes corresponding to vertices A, B, C, respectively,
D, E, F - midpoints of BC, CA, AB, respectively,
P, Q, R - feet of altitudes ha, hb, hc, respectively,
H - orthocenter of ABC,
O - the center of the circumscribed circle, O' - the center of the Euler circle,
K, L, M - midpoints of AH, BH, CH, respectively.
Being that KE is the medial line of the triangle AHC, KE || CH holds. Also, DE is
medial line of the triangle ABC, so DE || AB holds. Being that CH is perpendicular on AB, it
follows that KE is perpendicular on DE, so angle DEK is right. Being that Euler circle is
circumscribed around right triangle DEK, the center of the Euler circle is the midpoint
of hypotenuse of the triangle DEK, so KD is diameter and KO'=O'D and B(K, O', D) holds.
Point O' is the intersection of bisectors of segments PD and QE. These bisectors contain
bimedians of right trapeziums DOHP and EQHO, so point O' is the midpoint of their
common side HO. Being that KO' is the medial line of the triangle AOH, KO’ || AO holds,
so KD || AO and KD=AO hold. Also, AK || OD (they are both perpendicular on BC), so
quadrilateral AKDO is a parallelogram, it follows AK=OD (AK=1/2AH holds), so finally AH=2OD
holds. QED
|
Analysis |
|
Let us suppose that the triangle ABC fulfills the conditions of the problem. Let H be the
orthocenter of this triangle. Let D be the foot of the perpendicular from vertex O on BC.
On the basis Lemma, AH=2OD holds.
|
Construction |
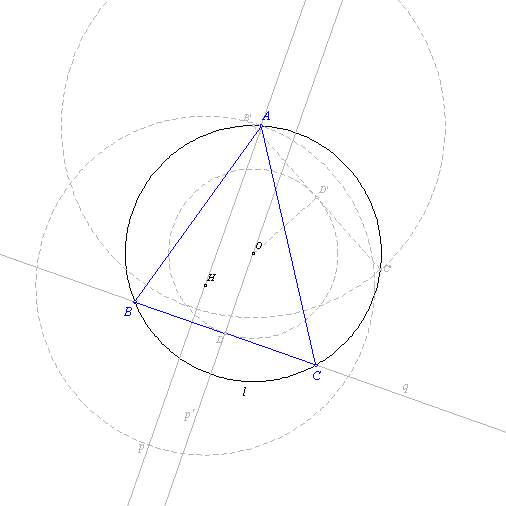
Let us select a random point of the circle l and denote it by B'.
Let us denote by C'
the point of the circle l such that B'C'=a holds.
Let us construct the perpendicular
from the center O of the given circle to the line B'C' at the point D'.
Let us denote
by A the point of the circle l such that AH=2OD' holds. Let us construct a line containing
point O which is parallel to AH.
Let us denote by D the point such that OD=OD' holds.
Let us construct a perpendicular on OD, containing D.
Let us denote by B and C the
intersection points of that perpendicular and the circle l.
Proof
The triangle BCO is congruent to the triangle B'C'O (the triangles BOD, COD, B'OD' and C'OD'
are congruent among themselves (OD=OD' holds on the basis of the construction, they all have
right angle at the vertex D or D' on the basis of the construction, and OB=OC=OB'=OC'=R,
where R is the radius of the circle l)), so BC=B'C' holds and B'C'=a holds on the basis of
the construction, therefore it follows that BC=a. On the basis of the construction point O
is the center of the circle l, AH || OD and OD is perpendicular on BC, so it follows that AH
is perpendicular on BC, and so H belongs to the altitude ha. Being that AH=2OD holds on
the basis of the construction, using the Lemma, it follows that the point A lies on the
circle l and H is the orthocenter. Points B and C lie on the circle l on the basis of the
construction. It follows that the triangle ABC with the orthocenter H is inscribed in
circle l. Therefore, the constructed triangle ABC fulfills the conditions of the problem.
|
|
|
|
Discussion |
|
The solution exists if and only if the segment a is smaller than the diameter of the
given circle l. Also, |R-OH|<=2OD<=R+OH must hold.
|
 |
In order to see the solution of this problem using GCLC, download .gcl code or look
at the html page with the same code:
|
|
|
|
|
|
|
