
Zadaci u ovom poglavlju za teorijsku podlogu imaju rezultate predstavljene na IX i X dvocasu predavanja i izlozene u knjizi "Algoritmika" u poglavlju 7, 8, 10!!! Pre njihove izrade NEOPHODNO je poznavanje prikazanih rezultata.
G1
Konstruisati algoritam linearne složenosti koji utvrđuje da li je zadatih n tačaka u ravni kolinearno.
R(ešenje)
Algoritam Kolinearne (p1,p2,...,pn)
input: p1,p2,...,pn /* tačke u ravni zadate parovima koordinata*/
output: kolinearne /* 0/1 */
{
kolinearne=1;
j=3;
while ( (kolinearne == 1) && (j<=n))
{
/* da li su (x1,y1) , (x2,y2), (xj,yj) kolinearne? */
if ((y2-y1)*(xj-x1) != (yj-y1)*(x2-x1)) kolinearne=0;
j++;
}
}
G2
Konstruisati algoritam linearne složenosti koji za datih n tačaka i datu pravu p pronalazi pravu paralelnu sa p koja dati skup tačaka deli na dva podskupa jednake veličine (tačka prave se može uračunati u bilo koji od podskupova).

R
Jednačina prave p: y=ax + m
Jednačina prave q paralelne sa p: y=ax + m'
Za k=1..n rastojanje tačke A(xk,yk) od tačkeA'(xk,axk + m')
(A' je projekcija od A u vertikalnom smeru na pravu q u pravcu y-ose)
jeste:
d(A,A')=dk=yk-axk -m' (dkje pozitivno/negativno ako je tačka iznad/ispod prave q)
Da bi se zadovoljio zahtev iz formulacije onda se m' bira tako da polovina brojeva dk bude veća ili jednaka od nule. Zapravo to znači da polovina brojeva yk-axk će biti veća ili jednaka od m' .
Otuda, za k=1..n se problem svodi na traženje medijane za yk-axk,o čemu je bilo reči kod rangovskih statistika u petoj glavi.
G3
Konstruisati algoritam linearne složenosti koji za datih n zgrada (datih svojim x,y koordinatama na mapi grada) i za datu tramvajsku prugu u vidu prave p pronalazi novu prugu paralelnu sa datom koja dati skup zgrada deli na dva podskupa jednake veličine (voditi racuna da ni stara ni nova pruga ne prolaze korzo zgradu).
G4
a) Za tačku P u ravni se kaže da dominira
nad tačkom Q ako su x i y koordinata tačke P veće od odgovarajućih
koordinata tačke Q. Tačka P je maksimalna u datom skupu tačaka S ako
ni jedna tačka iz S ne dominira nad njom. Konstruisati algoritam složenosti O (n log n )
za nalaženje svih maksimalnih tačaka datog skupa S od n tačaka.
b) Rešiti odgovarajući problem u tri dimenzije (definicija dominacije će se odnositi na sve tri koordinate).
R
a)
Mogu u skupu i sve tačke da budu maksimalne.
Ako su sve tačke
različite, mora bar jedna da bude maksimalna
(SP: ako tačka nije max, onda postoji neka koja njom dominira, pa je ona max ili ne ,...)
Lema 1: Ako tačka P nije max, onda njom dominira neka max tačka.
Lema2: Ako skupu tačaka S dodamo novu tačku R koja ne dominira niti jednom od starih max tačaka za k=1..n: M12,..., Mk iz S, onda one ostaju maksimalne, a nova tačka R maksimalna ako njom ne dominira nijednaod starih maksimalnih tačaka.
Lema3: Ako ima više tačaka sa istom x koordinatom,onda eventualno maksimalna tačka može
biti samo ona sa najvećom y koordinatom.
b)
G5
Dat je skup intervala na pravoj, predstavljenih koordinatama krajeva.
Konstruisati algoritam složenosti O (n log n ) za nalaženje svih intervala
koji se sadrže u nekom drugom intervalu iz skupa.
R
Algoritam IntervaliPresek (parovi koordinata levih i desnih krajeva duži)
Ulaz: (l1,r1), ..., (ln,rn) /*parovi koordinata levih i desnih krajeva duži*/
Izlaz: (lk,rk)
/*parovi koordinata levih i desnih krajeva duži koje se sadrže u drugoj duži */
Ideja: duž nije sadržana u drugoj duži ako je levi kraj duži manji od
levog kraja druge duži
ili je desni kraj duži veći od desnog kraja druge duži.
POJAČANA IH: U skupu sa manje od n duži umemo da odredimo i
označimo duži koje su sadržane u nekoj drugoj duži istog skupa i
umemo da odredimo do tada najveći desni kraj
Opis algoritma:
1. sortiranje duži u rastućem poretku po njihovim levim krajevima
(ako dve duži imaju isti levi kraj, dodatno se sortiraju po
desnim krajevima u opadajućem poretku )
2. u prvom koraku ne biva markirana prva duž (jer nije sadržana ni
u jednoj duži, jer desni krajebi duži su u opadajućem poretku ako im je jednak
levi kraj), a do tada najveći desni kraj duži je vrednost desnog kraja
prve duži
3. pretpostavimo da je problem rešen za prvih n-1 duži (tako što su markirane sve
duži koje su sadržane u nekoj drugoj duži i da je poznat do tada najveći
desni kraj za tih n-1 duži)
4. Razmotrimo n-tu duž:
Ako je njen desni kraj veći od do tada najvećeg desnog kraja, onda ona nije
sadržana ni u jednoj duži, te je ne markiramo i njen desni kraj stavimo za
do tada najveći desni kraj.
U suprotnom, ta duž je sadržana u drugoj duži, te je markiramo.
(BSO pretpostavimo da ne postoje duži čiji su i levi i desni krajevi jednaki). Nakon primene algoritma markirane su duži koje su sadržane u drugoj.
G6
Dato je n pravougaonika sa stranicama paralelnim osama. Konstruisati algoritam složenosti O(n log n) za nalaženje pravougaonika sadržanih u nekom drugom pravougaoniku.
R
Uputstvo: iskoristiti zadatke G4 i G5
| A1 Navesti primer izracunavanja nk (k > 10) sa manjim brojem množenja nego u algoritmu Stepen_kvadriranjem (n, k) u glavi 8.2. |
PODSECANJE NA REZULTAT IZLOZEN NA PREDAVANJIMA: I algoritam:
Algoritam Stepen (n,k) (glava 8.2) nk=n*nk-1=> O(k)
| II algoritam: Algoritam Stepen_kvadriranjem (n,k) (glava 8.2) | n k=(nk/2)2 , k jeparan broj |
| n k=n*(n(k-1)/2)2 , k je neparan broj | |
| T(k)=T(k/2) + 1 => a=1, b=2, O(k0 log k), tj. O(log k) | |
Broj množenja ne zavisi od n (zavisi od k). REŠENJE:
Pogledajmo primer najmanjeg k koje ispunjava uslov iz formulacije k > 10 i k=2m-1,tj. m=4, k=15: Stepen_kvadriranjem (n, k) za k=15: n15= n* (n7)2=n* (n*n6)2= . . . = n* ( n* (n*n2)2) 2 => šest množenja REŠENJE:
Na primer: 18 = 13 + 5 (2 sabirka, dok log2 18 > 2)
a) Dokaz principom matematičke indukcije: baza: n=3 F(1)=F(2)=1, F(3)=2, F(4)=3 => n=F(4) && 1<log2 3 Dokaz: Po (IH) za broj (n-F(k))potrebno je <= log2 (n-F(k)) razl. Fibonač. brojeva b) Algoritam Predstava (n)
REŠENJE: Algoritam vrsta * kolona zahteva n3množenja,Vinogradov algoritam n3/2 + n2 množenja.
Brute-force tehnika: izvrsiti proveru svih troclanih podskupova skupa cvorova.
Algoritam NZD (a0, a1)
{ Na primer: 57*x + 33*y = 3
Ako se više puta pojavljuje drugi slučaj nk=n*(n(k-1)/2)2,k je neparan broj, onda ukupan broj množenja je veci, a najgori slucaj je za k=2m-1 (tj. cesta pojava drugog slucaja).
Ali, na primer n15=( ( (n2 ) 2 * n)3 => pet množenja
A2
Fibonacijevi brojevi su definisani sledecom diferencnom jednacinom:
F( n ) = F( n-1 ) + F( n-2 ), ( n > 2 )
F(1) = F(2) = 1
Dokazati da se svaki prirodan broj n > 2 može predstaviti u obliku zbira najviše log2 n različitih Fibonacijevih brojeva.
b) Konstruisati algoritam za odredivanje takve predstave datog broja n.
induktivna hipoteza: Za sve brojeve k manje od n važi
(IH) prirodan broj k > 2 može se predstaviti u obliku zbira najviše log2k-1 Fibonacijevih brojeva
Dakle,postoji k: F(k)<=n<F(k+1) =>F(k) > n/2
/* supr. pretp. F(k)<=n/2. Kako je F(k-1) < F(k) za k>2, onda je F(k-1) < n/2
Odatle, F(k+1)=F(k)+F(k-1) < n/2 + n/2 =n što je kontradikcija sa n< F(k+1) */
Kako je n-F(k)< F(k), /* jer iz gore dokaznog svojstva F(k) > n/2 => 2*F(k)>n => F(k) > n-F(k)) */
onda F(k) ne učestvuje u reprezentaciji broja n-F(k) Fibonačijevim brojevima, te se za broj n= F(k) + (n-F(k))
koristi <= 1 + log2 (n-F(k)) razl. Fibonač. brojeva.
Kako 1+ log2 (n-F(k))=log22 + log2(n-F(k))=log2(2n - 2 F(k)) = log2(n + ( n- 2F(k))< log2n (jer n-2F(k) <0 po gore dokazanom)
input: n /* n>2 */
output: reprezentacija broja n kao sume Fibonačijevihbrojeva*/
{
f1=1; f2=1;
while (f2 <= n) {d=f1+f2; f1=f2; f2=d;} /* naci k: f(k)<=n < f(k+1) */
while (n>0) { if (n-f1>=0) { stampaj f1; n=n-f1;} d=f2-f1; f2=f1; f1=d;}
}
A3
Pokazati kako se kvadrat kvadratne matrice reda dva može izracunati pomocu pet množenja.
Za n=2 to je 8 množenja. Štrasen je otkrio da je potrebno sedam množenja elemenata da bi se izracunao proizvod ma koje dve matrice reda dva. (obavezno pogledati poglavlje 8.5.2)
Ako se radi o množenju dve iste matrice reda dva,tj. kvadriranju, onda je dovoljno izracunati pet proizvoda:
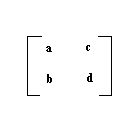

= 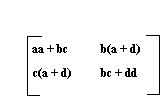
A4
Dat je neusmereni povezani graf G=(V,E) sa n cvorova.
Potrebno je ustanoviti da li u G postoji trougao (tj. takva tri cvora
da između svaka dva od njih postoji grana).
Konstruisati algoritam slozenosti O(nlog2 7)
koji daje odgovor na ovo pitanje.
Podskupova ima n(n-1)(n-2)/6, a kako se za svaki od njih moze proveriti za konstantno vreme da li jeste ili nije trougao, vremenska slozenost ovog algoritma je O(n3).
Dakle, slozenost je veca od one koje se trazi u zadatku!!! Moze li drukcije?
A5
Euklidov algoritam odreduje najveci zajednicki delilac za prirodne brojeve a0, a1. Na osnovu ideje Euklidovog algoritma, konstruisati algoritam koji pronalazi bar jedno celobrojno rešenje jednacine a0*x+ a1*y = NZD(a0,a1).
input: a[0], a[1]
output: x, y
i=0; x[i]=1; y[i]=0;
i=1; x[i]=0; y[i]=1;
while ( a[i-1] % a[i] != 0)
{ q=a[i-1] / a[i];
a[i+1]= a[i-1]- q* a[i];
x[i+1]= x[i-1]- q* x[i];
y[i+1]= y[i-1]- q* y[i];
i++;
}
stampaj x[i], y[i]
}
| i | a[i] | x[i] | y[i] |
| 0 | 57 | 1 | 0 |
| 1 | 33 | 0 | 1 |
| 2 | 24 | 1 | -1 |
| 3 | 9 | -1 | 2 |
| 4 | 6 | 3 | -5 |
| 5 | 3 | -4 | 7 |
Dakle, x=-4, y=7
Da li je za svako i>=0 ispunjeno a[0]*x[i] + a[1]*y[i]=a[i] ?
DZ
i=0 => a[0]*x[0] + a[1]*y[0]=a[0]*1+0=a[0]
i=1 => a[0]*x[1] + a[1]*y[1]=0+a[1]*1=a[1]
IH: pretp. da važi za i-1, i, i>=2
Po algoritmu: x[i+1]= x[i-1] - q* x[i];
y[i+1]= y[i-1] - q* y[i];
Dakle, a[0]*x[i+1] + a[1]*y[i+1]= a[0] * (x[i-1] - q* x[i]) + a[1] * (y[i-1] - q* y[i]) =
a[0]*x[i-1] +a[1]*y[i-1] -
- q * (a[0]*x[i] + a[1]*y[i]) = a[i-1] -q* a[i] = (po IH) a[i+1] => Q.E.D.
G7
Opisati algoritam svođenja problema sadržanih intervala (zadatak G5)na problem određivanja maksimalne tačke
(zadatak G4).
R
Neka je skup intervala na pravoj/duži Di zadat skupom parova (Li,Ri).
Ideja je da se svakom i-tom intervalu/svakoj i-toj duži pridruži tačka Pi sa koordinatama (-Li,Ri).
Lema1: Tačka Pi dominira tačkom Pk ako i samo ako je duž Dk sadržana u duži Di.
D1: Tacka Pi=(-Li,Ri) dominira tačkom Pk=(-Lk,Rk )
ako i samo ako vazi -Lk <= - Li && Rk <= Ri
tj. ako i samo ako vazi Lk >= Li && Rk >= Ri
tj. ako i samo ako je duž Dk sadržana u duži Di.
Dakle, duž Dk je sadržana u nekoj duži ako i samo ako tačka Pk nije maksimalna.
Time je problem određivanja sadržanih duži sveden na problem određivanje maksimalnih duži.
M1
Dokazati da ako postoji algoritam složenosti O(T(n)) za množenje kvadratne n×n donje trougaone matrice kvadratnom n×n gornje trougaonom matricom, onda postoji algoritam složenosti O(T(n)+n2) za množenje dve proizvoljne n×n matrice. Pretpostaviti da T(cn)=O(T(n)) za proizvoljnu konstantu c > 0.
REŠENJE:
Neka su A i B dve proizvoljne kvadratne matrice reda n .
Svaka od njih se moze predstaviti kao zbir po jedne gornje
i po donje trougaone matrice (TA, BA, TB, BB, redom):
A= T A + B A
B= T B + B B
Dalje je : AB=( T A + B A ) ( T B + B B )=T AT B + B AB B + B AT B + T AB B
Ako se upotrebi algoritam iz formulacije zadataka mogu\ce je izracunati proizvod :
| BA 0
T A BA |
× |
TB BB
0 TB |
= |
B AT B BABB T AT B B AT B + T AB B |
Kao rezultat dobija se matrica koja sadrzi blokove: B AB B , T AT B , B AT B + T AB B
Ovi blokovi ucestvuju u izracunavanju proizvoda A × B.
Na taj nacin se problem izracunavanja proizvoda dve proizvoljne matrice svodi na problem izracunavanja proizvoda kvadratne donje trougaone matrice kvadratnom gornjom trougaonom matricom.
Ukupno vreme izvršavanja : O(T(2n)+n2 )=O(T(n)+n2)
M2 Ako je dat algoritam za mnozenje dve n * n donje trougaone matrice čije vreme izvrsavanja je O(T(n)), dokazati da postoji algoritam za mnozenje dve proizvoljne n *n matrice cije vreme izvrsavanja je O(T(n)+n2 ). (Moze se pretpostaviti da je T(cn)=O(T(n)) za svaku konstantu c)
REŠENJE: Neka su A i B dve proizvoljne kvadratne matrice reda n .
A= T A + B A
B= T B + B B
Dalje je : AB=( T A + B A ) ( T B + B B )=T AT B + B AB B + B AT B + T AB B
Ako se upotrebi algoritam iz formulacije zadataka mogu\ce je izracunati proizvod :
| BA 0
T A BA |
× |
BB 0
TB BB |
= |
B AB B 0 T AB B+B AT B B AB B |
Kao rezultat dobija se matrica koja sadrzi blokove: B AB B , T AT B , B AT B + T AB B
Ovi blokovi ucestvuju u izracunavanju proizvoda A × B.
Matrice ( TA )T i ( TB )T su donje trougaone matrice, te se upotrebom datog algoritma moze izracunati
blok T A T B na sledeci nacin:
T A T B = ( ( TB )T
( TA )T )T
Ukupno vreme izvršavanja je O(T(2n)+n2)= O(T(n)+n2).
Na taj nacin se problem izracunavanja proizvoda proizvoljne dve matrice svodi na problem izracunavanja proizvoda
dve kvadratne donje trougaone matrice.