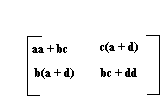Algoritamske strategije (algebarski algoritmi)
Zadaci u ovom poglavlju za teorijsku podlogu imaju rezultate predstavljene na IX i X dvocasu predavanja i izlozene u knjizi "Algoritmika"
u poglavlju 8!!! Pre njihove izrade NEOPHODNO je poznavanje prikazanih rezultata.
Algebarski algoritmi
A1
Navesti primer izračunavanja nk (k > 10) sa manjim brojem množenja nego u algoritmu Stepen_kvadriranjem (n, k) u glavi 8.2.
|
PODSECANJE NA REZULTAT IZLOZEN NA PREDAVANJIMA: I algoritam: Algoritam Stepen (n,k) (glava 8.2) nk=n*nk-1=> O(k)
| II algoritam: Algoritam Stepen_kvadriranjem (n,k) (glava 8.2) | nk=(nk/2)2 , k jeparan broj |
| nk=n*(n(k-1)/2)2 , k je neparan broj |
| T(k)=T(k/2) + 1 => a=1, b=2, O(k0 log k), tj. O(log k) |
Broj množenja ne zavisi od n (zavisi od k).
Ako se više puta pojavljuje drugi slučaj nk=n*(n(k-1)/2)2,k je neparan broj, onda ukupan broj množenja je veći, a najgori slučaj je za k=2m-1 (tj. česta pojava drugog slučaja).
|
REŠENJE:
Pogledajmo primer najmanjeg k koje ispunjava uslov iz formulacije k > 10 i k=2m-1,tj. m=4, k=15: Stepen_kvadriranjem (n, k) za k=15: n15= n* (n7)2=n* (n*n6)2= . . . = n* ( n* (n*n2)2) 2 => šest množenja
Ali, na primer n15=( ( (n2 ) 2 * n)3 => pet množenja
|
A2
Fibonačijevi brojevi su definisani sledećom diferencnom jednačinom:
F( n ) = F( n-1 ) + F( n-2 ), ( n > 2 )
F(1) = F(2) = 1
Dokazati da se svaki prirodan broj n > 2 može predstaviti u obliku zbira najviše log2 n različitih Fibonačijevih brojeva.
b) Konstruisati algoritam za određivanje takve predstave datog broja n.
|
REŠENJE:
Na primer: 18 = 13 + 5 (2 sabirka, dok log2 18 > 2)
a) Dokaz principom matematičke indukcije:
baza: n=3 F(1)=F(2)=1, F(3)=2, F(4)=3 => n=F(4) && 1<log2 3
induktivna hipoteza: Za sve brojeve k manje od n važi
(IH) prirodan broj k > 2 može se predstaviti u obliku zbira najviše log2k-1 Fibonačijevih brojeva
Dokaz:
Dakle,postoji k: F(k)<=n<F(k+1) =>F(k) > n/2
/* supr. pretp. F(k)<=n/2. Kako je F(k-1) < F(k) za k>2, onda je F(k-1) < n/2
Odatle, F(k+1)=F(k)+F(k-1) < n/2 + n/2 =n što je kontradikcija sa n< F(k+1) */
Po (IH) za broj (n-F(k))potrebno je <= log2 (n-F(k)) razl. Fibonač. brojeva
Kako je n-F(k)< F(k), /* jer iz gore dokaznog svojstva F(k) > n/2 => 2*F(k)>n => F(k) > n-F(k)) */
onda F(k) ne učestvuje u reprezentaciji broja n-F(k) Fibonačijevim brojevima, te se za broj n= F(k) + (n-F(k))
koristi <= 1 + log2 (n-F(k)) razl. Fibonač. brojeva.
Kako 1+ log2 (n-F(k))=log22 + log2(n-F(k))=log2(2n - 2 F(k)) = log2(n + ( n- 2F(k))< log2n (jer n-2F(k) <0 po gore dokazanom)
b)
Algoritam Predstava (n)
input: n /* n>2 */
output: reprezentacija broja n kao sume Fibonačijevihbrojeva*/
{
f1=1; f2=1;
while (f2 <= n) {d=f1+f2; f1=f2; f2=d;} /* naci k: f(k)<=n < f(k+1) */
while (n>0) { if (n-f1>=0) { stampaj f1; n=n-f1;} d=f2-f1; f2=f1; f1=d;}
}
A3
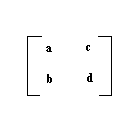
Pokazati kako se kvadrat kvadratne matrice reda dva može izračunati pomoću pet množenja.
|
REŠENJE:
Algoritam vrsta * kolona zahteva n3množenja,Vinogradov algoritam n3/2 + n2 množenja.
Za n=2 to je 8 množenja. Štrasen je otkrio da je potrebno sedam množenja elemenata da bi se izračunao proizvod ma koje dve matrice reda dva. (obavezno pogledati poglavlje 8.5.2)
Ako se radi o množenju dve iste matrice reda dva,tj. kvadriranju, onda je dovoljno izračunati pet proizvoda:
- a2
- bc
- d2
- b(a+d)
- c(a+d)
|
A4
Dat je neusmereni povezani graf G=(V,E) sa n cvorova.
Potrebno je ustanoviti da li u G postoji trougao (tj. takva tri cvora
da između svaka dva od njih postoji grana).
Konstruisati algoritam slozenosti O(nlog2 7)
koji daje odgovor na ovo pitanje.
|
REŠENJE:
Brute-force tehnika: izvrsiti proveru svih troclanih podskupova skupa cvorova.
Podskupova ima n(n-1)(n-2)/6, a kako se za svaki od njih moze proveriti za konstantno vreme da li jeste ili nije trougao, vremenska slozenost ovog algoritma je O(n3).
Dakle, slozenost je veca od one koje se trazi u zadatku!!! Moze li drukcije?
A5
Euklidov algoritam određuje najveći zajednički delilac za prirodne brojeve a0, a1. Na osnovu ideje Euklidovog algoritma, konstruisati algoritam koji pronalazi bar jedno celobrojno rešenje jednačine a0*x+ a1*y = NZD(a0,a1).
|
Algoritam NZD (a0, a1)
input: a[0], a[1]
output: x, y
{
i=0; x[i]=1; y[i]=0;
i=1; x[i]=0; y[i]=1;
while ( a[i-1] % a[i] != 0)
{ q=a[i-1] / a[i];
a[i+1]= a[i-1]- q* a[i];
x[i+1]= x[i-1]- q* x[i];
y[i+1]= y[i-1]- q* y[i];
i++;
}
stampaj x[i], y[i]
}
Na primer: 57*x + 33*y = 3
| i | a[i] | x[i] | y[i] |
| 0 | 57 | 1 | 0 |
| 1 | 33 | 0 | 1 |
| 2 | 24 | 1 | -1 |
| 3 | 9 | -1 | 2 |
| 4 | 6 | 3 | -5 |
| 5 | 3 | -4 | 7 |
Dakle, x=-4, y=7
Da li je za svako i>=0 ispunjeno a[0]*x[i] + a[1]*y[i]=a[i] ?
DZ
i=0 => a[0]*x[0] + a[1]*y[0]=a[0]*1+0=a[0]
i=1 => a[0]*x[1] + a[1]*y[1]=0+a[1]*1=a[1]
IH: pretp. da važi za i-1, i, i>=2
Po algoritmu: x[i+1]= x[i-1] - q* x[i];
y[i+1]= y[i-1] - q* y[i];
Dakle, a[0]*x[i+1] + a[1]*y[i+1]= a[0] * (x[i-1] - q* x[i]) + a[1] * (y[i-1] - q* y[i]) =
a[0]*x[i-1] +a[1]*y[i-1] -
- q * (a[0]*x[i] + a[1]*y[i]) = a[i-1] -q* a[i] = (po IH) a[i+1] => Q.E.D.
Redukcija ili svođenje nekih problema na već rešavane
Korisno je utvrditi može li se zadati problem rešiti ako se zna rešenje
njemu sličnog problema. Mada ponekad put do utvrđivanja sličnosti dva problema vodi kroz složen proces redukcije zadatog problema na prethodno poznati problem. Naročito su interesantne redukcije među grafovskim algoritmima i grafovskim i matričnim algoritmima, kao i rešavanje problema linearnog i celobrojnog programiranja.
Primena dvodimenzionalnog niza, matrica
M1
Dokazati da ako postoji algoritam složenosti O(T(n)) za
množenje kvadratne n×n donje trougaone matrice kvadratnom
n×n gornje trougaonom matricom, onda postoji algoritam složenosti O(T(n)+n2) za množenje dve proizvoljne
n×n matrice. Pretpostaviti da T(cn)=O(T(n)) za proizvoljnu konstantu
c > 0.
REŠENJE:
Neka su A i B dve proizvoljne kvadratne matrice reda n .
Svaka od njih se moze predstaviti kao zbir po jedne gornje
i po donje trougaone matrice (TA, BA, TB, BB, redom):
A= T A + B A
B= T B + B B
Dalje je : AB=( T A + B A ) ( T B + B B )=T AT B + B AB B + B AT B + T AB B
Ako se upotrebi algoritam iz formulacije zadataka mogu\ce je izracunati
proizvod :
BA 0
T A BA
|
×
|
TB BB
0 TB
|
=
|
B AT B BABB
T AT B B AT B + T AB B
|
Kao rezultat dobija se matrica koja sadrzi blokove:
B AB B , T AT B ,
B AT B + T AB B
Ovi blokovi ucestvuju u izracunavanju proizvoda A × B.
Na taj nacin se problem izracunavanja proizvoda dve proizvoljne matrice svodi na problem izracunavanja proizvoda kvadratne donje trougaone matrice kvadratnom gornjom trougaonom matricom.
Ukupno vreme izvršavanja : O(T(2n)+n2 )=O(T(n)+n2)
M2
Ako je dat algoritam za mnozenje dve n * n donje trougaone matrice čije vreme izvrsavanja je O(T(n)),
dokazati da postoji algoritam za mnozenje dve proizvoljne n *n matrice cije vreme izvrsavanja je
O(T(n)+n2 ). (Moze se pretpostaviti da je T(cn)=O(T(n)) za svaku konstantu c)
REŠENJE:
Neka su A i B dve proizvoljne kvadratne matrice reda n .
Svaka od njih se moze predstaviti kao zbir po jedne gornje
i po jednedonje trougaone matrice(TA, BA, TB, BB, redom):
A= T A + B A
B= T B + B B
Dalje je : AB=( T A + B A ) ( T B + B B )=T AT B + B AB B + B AT B + T AB B
Ako se upotrebi algoritam iz formulacije zadataka mogu\ce je izracunati
proizvod :
BA 0
T A BA
|
×
|
BB 0
TB BB
|
=
|
B AB B 0
T AB B+B AT B B AB B
|
Kao rezultat dobija se matrica koja sadrzi blokove:
B AB B , T AT B ,
B AT B + T AB B
Ovi blokovi ucestvuju u izracunavanju proizvoda A × B.
Matrice ( TA )T i ( TB )T su donje trougaone matrice, te se upotrebom datog algoritma moze izracunati
blok T A T B na sledeci nacin:
T A T B = ( ( TB )T
( TA )T )T
Ukupno vreme izvršavanja je O(T(2n)+n2)= O(T(n)+n2).
Na taj nacin se problem izracunavanja proizvoda proizvoljne dve matrice svodi na problem izracunavanja proizvoda
dve kvadratne donje trougaone matrice.
M3 - samo za radoznale
Formirati algoritam koji za dve reči dužine n (prva reč), m
(druga reč) nad azbukom slova i cifara pronalazi
niz operacija editovanja najmanje cene kojim se prva reč transformiše u drugu reč.
Dozvoljene su tri vrste operacija editovanja i svaka ima cenu jedan:
insert = umetanje jednog karaktera
delete = brisanje 1 karaktera
replace = zamena jednog karaktera drugim karakterom
Primer za A=maak, B=amaa
A(1)=amaak /*insert a*/
A(2)=amaa /*delete k */
CENA: 1+1=2
A(1)=aak /*delete m*/
A(2)=amak /*insert m */
A(3)=amaa
/*replace k slovom a */
CENA: 1+1+1=3
Operacija editovanja najmanje cene zapravo predstavlja
Levenshtein ili
edit rastojanje dve niske. Nazvana je po ruskom naučniku
Vladimiru Levenshtein-u koji se 1965. bavio ovim rastojanjem.
Koristi se u aplikacijama u kojima je potrebno znati koliko su slične dve
niske, npr.
spell checker-i (provera pravopisa)
Spell checkeri porede reč sa ulaza sa jedinicom rečnika.Ako reč nije pronađena u rečniku, smatra se da nije korektno uneta i izlistavaju se moguće rečiiz rečnika, počev od onih sa najmanjom Levenshtein udaljenosti od ulazne reči. aplikacije molekularne biologije (DNK analiza; što je veći stepen sličnosti dve sekvence, bilo DNK, RNK ili amino-kiselina, to im je sličnija i funkcija ili struktura, npr. kod multiplskleroze koja to bakterijska ili virusna sekvenca iz ranije infekcije je slična sekvenci proteinske mijelinske ovojnice )
detekcija plagijata
prepoznavanje govora
Što je Levenštajnovo rastojanje dve niske veće, to se one više razlikuju među sobom.
Procena sličnosti dve niske može se utvrditi na osnovu Levenštajnovog rastojanja ili LCS algoritmom koji pronalazi najduužu zajedničku podsekvencu (podsekvenca se dobija iz niske brisanjem 0 ili više karaktera). Oba algoritma će biti navedena kao ilustracija tehnike dinamičkog programiranja.
Inače, današnje softverske alatke koriste više metrika, a često i njihovu kombinaciju. Neke metrike su pogodnije za oblast molekularne biologije, neke za oblast text mining-a. Više o metrikama nad niskama može se pogledati u lekciji
Metrike nad niskama.
Oznake: Neka je A(k) niz koji se sastoji od prvih k elemenata niza A.Neka je B(k) niz koji se sastoji od prvih k elemenata niza B.
Nizovi edit operacija koji transformišu A(i) u B(j) zavisno od poslednje operacije u nizu edit operacija
Postoje tri ključne situacije:- ako je A(i-1) transformisan u B(j), onda se obavlja delete znaka a[i]
- ako je A(i) transformisan u B(j-1), onda se obavlja insert znaka b[j]
- ako je A(i-1) transformisan u B(j-1), onda se obavlja replace znaka a[i] (istim ili različitim) znakom b[j]
Dakle, najmanja cena transformacije A(i) u B(j), tj. Cena[i,j] jednaka je Cena[i,j]=Min_3_broja (c1, c2, c3),gde - c1 - slučaj prethodnog delete a[i], c1= Cena[i-1,j]+1
- c2 - slučaj prethodnog insert b[j], c2= Cena[i,j-1]+1
- c3 - slučaj prethodnog replace a[i] sa b[j], c3= Cena[i-1,j-1]+ (a[i]==b[j])
pseudo-jezik:
Algoritam NajjeftinijeEditovanje (a, b, n, m)
ulaz: a, n, b, m
izlaz: Cena /* tabela (n+1)*(m+1) */
{
/* i, j su lokalne promenljive i imaju ulogu brojača u petljama
Potez je matrica koju pregledamo unazad (počev od Potez[n,m]), ne bi li dobili konačan niz operacija editovanja.
Potez[i,j] poslednja operacija (delete ili insert ili replace) editovanja koja se obavlja da bi Cena[i,j] bila minimalna c1 - slučaj prethodnog delete a[i]
c2 - slučaj prethodnog insert b[j]
c3 - slučaj prethodnog replace a[i] sa b[j]
*/
/* transformacija prefiksa A(i) u praznu nisku B(0) */
for (i=0; i <= n; i++)
{
Cena[i,0]=i;
Potez[i,0]= delete;
}
/* transformacija praznog prefiksa A(0) u prefiks B(j) */
for (j=0; j <= m; j++)
{
Cena[0,j]=j;
Potez[0,j]= insert;
}
/* i!=0, j!=0 i najjeftinija transformacija A(i) u B(j) */
for (i=1; i <= n; i++)
for (j=1; j <= m; j++)
{
c1= Cena[i-1,j]+1;
c2= Cena[i,j-1]+1;
if (a[i]==b[j])
c3= Cena[i-1,j-1];
else
c3= Cena[i-1,j-1]+1;
Cena[i,j]=Min_3_broja (c1, c2, c3);
Potez[i,j] = izabrana_operacija_editovanja_u_Min_3_broja;
} /*for */
} /*KRAJ*/
Procena složenosti
Svaki element matrice Cena se i izračunava za konstantno vreme, pa je vremenska složenost algoritma O(mn), dok je i prostorna složenost O(mn). Može se postići prostorna složenost reda O(m), ali ako se matrica Cena popunjava po vrstama (jer jedna vrsta zavisi samo od prethodne vrste).
Primer
Primer formiranja matrice cena za niske "SAMBA" i "SIMBAD".
Koraci 1, 2
| | | S | A | M | B | A |
| | 0 | 1 | 2 | 3 | 4 | 5 |
| S | 1 | | | | | |
| I | 2 | | | | | |
| M | 3 | | | | | |
| B | 4 | | | | | |
| A | 5 | | | | | |
| D | 6 | | | | | |
Koraci od 3 do 6 kada i = 1
| | | S | A | M | B | A |
| | 0 | 1 | 2 | 3 | 4 | 5 |
| S | 1 | 0 | | | | |
| I | 2 | 1 | | | | |
| M | 3 | 2 | | | | |
| B | 4 | 3 | | | | |
| A | 5 | 4 | | | | |
| D | 6 | 5 | | | | |
Koraci od 3 do 6 kada i = 2
| | | S | A | M | B | A |
| | 0 | 1 | 2 | 3 | 4 | 5 |
| S | 1 | 0 | 1 | | | |
| I | 2 | 1 | 1 | | | |
| M | 3 | 2 | 2 | | | |
| B | 4 | 3 | 3 | | | |
| A | 5 | 4 | 4 | | | |
| D | 6 | 5 | 5 | | | |
Koraci od 3 do 6 kada i = 3
| | | S | A | M | B | A |
| | 0 | 1 | 2 | 3 | 4 | 5 |
| S | 1 | 0 | 1 | 2 | | |
| I | 2 | 1 | 1 | 2 | | |
| M | 3 | 2 | 2 | 1 | | |
| B | 4 | 3 | 3 | 2 | | |
| A | 5 | 4 | 4 | 3 | | |
| D | 6 | 5 | 5 | 4 | | |
Koraci od 3 do 6 kada i = 4
| | | S | A | M | B | A |
| | 0 | 1 | 2 | 3 | 4 | 5 |
| S | 1 | 0 | 1 | 2 | 3 | |
| I | 2 | 1 | 1 | 2 | 3 | |
| M | 3 | 2 | 2 | 1 | 2 | |
| B | 4 | 3 | 3 | 2 | 1 | |
| A | 5 | 4 | 4 | 3 | 2 | |
| D | 6 | 5 | 5 | 4 | 3 | |
Koraci od 3 do 6 kada i = 5
| | | S | A | M | B | A |
| | 0 | 1 | 2 | 3 | 4 | 5 |
| S | 1 | 0 | 1 | 2 | 3 | 4 |
| I | 2 | 1 | 1 | 2 | 3 | 4 |
| M | 3 | 2 | 2 | 1 | 2 | 3 |
| B | 4 | 3 | 3 | 2 | 1 | 2 |
| A | 5 | 4 | 4 | 3 | 2 | 1 |
| D | 6 | 5 | 5 | 4 | 3 | 2 |
Korak 7
Rastojanje je u donjoj desnoj ćeliji, tj. 2, što odgovara i inuitivnoj realizaciji da se niska "SAMBA" može transformisati u nisku "SIMBAD" zamenom slova "A" slovom "I" i dodavanjem slova "D" (1 zamena i 1 umetanje = 2 operacije ).
Za razmisljanje:
A=aabccbba, B=baacbabacc, Cena=?