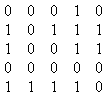
1. Primer predstavljanja grafa preko niza listi suseda svakog od čvorova grafa. U programu se unosi graf i DFS algoritmom se utvrđuje koji su čvorovi dostižni iz čvora 0.
#include <stdlib.h>
#include <stdio.h>
/* Cvor liste suseda */
typedef struct _cvor_liste
{ int broj; /* indeks suseda */
struct _cvor_liste* sledeci;
} cvor_liste;
/* Graf predstavlja niz pokazivaca na pocetke listi suseda */
#define MAX_BROJ_CVOROVA 100
cvor_liste* graf[MAX_BROJ_CVOROVA];
int broj_cvorova;
int posecen[MAX_BROJ_CVOROVA]; /* niz markiranih čvorova u DFS algoritmu */
/* Ubacivanje na pocetak liste */
cvor_liste* ubaci_u_listu(cvor_liste* lista, int broj)
{ cvor_liste* novi=malloc(sizeof(cvor_liste));
novi->broj=broj;
novi->sledeci=lista;
return novi;
}
/* Brisanje liste */
void obrisi_listu(cvor_liste* lista)
{ if (lista) { obrisi_listu(lista->sledeci); free(lista); }
}
/* Ispis liste */
void ispisi_listu(cvor_liste* lista)
{ if (lista) { printf("%d ",lista->broj); ispisi_listu(lista->sledeci); }
}
/* Rekurzivna implementacija DFS algoritma */
void poseti(int i)
{ cvor_liste* sused;
printf("Posecujem cvor %d\n",i);
posecen[i]=1;
for( sused=graf[i]; sused!=NULL; sused=sused->sledeci)
if (!posecen[sused->broj])
poseti(sused->broj);
}
main()
{ int i; /* brojac u ciklusu */
printf("Unesi broj cvorova grafa : "); scanf("%d",&broj_cvorova);
for (i=0; i<broj_cvorova; i++)
{ int br_suseda,j;
graf[i]=NULL;
printf("Koliko cvor %d ima suseda : ",i); scanf("%d",&br_suseda);
for (j=0; j<br_suseda; j++)
{ int sused;
do
{
printf("Unesi broj %d. suseda cvora %d : ",j+1,i); scanf("%d",&sused);
} while (sused<0 || sused>=broj_cvorova);
graf[i]=ubaci_u_listu(graf[i],sused);
}
}
for (i=0; i<broj_cvorova; i++)
{ printf("%d - ",i); ispisi_listu(graf[i]); printf("\n");}
poseti(0);
}
2. Napisati program koji učitava grane usmerenog grafa od n čvorova i za par datih čvorova (čvorovi su zadati rednim brojevima) ispisuje da li je jedan čvor dostupan iz drugog.
3. Čvor s usmerenog grafa G = (V,E) sa n čvorova se naziva ponor ako je ulazni stepen čvora s jednak n − 1 i njegov izlazni stepen jednak 0. Drugim rečima, za svaki čvor x iz skupa V različit od s postoji grana x → s i ne postoji grana s → x. Precizno opišite algoritam vremenske složenosti O(n) koji određuje da li usmereni graf G predstavljen matricom susedstva sadrži čvor koji je ponor.
Rešenje:
Primetimo da ako postoji grana između čvorova v i u, tada v ne može da bude ponor,
a ako grana ne postoji tada u ne može da bude ponor.
Ako je A matrica susedstva tada važi:
Ako je A[v][ u] == 1 tada čvor v nije ponor.
Ako je A[v][ u]= = 0 tada čvor u nije ponor.
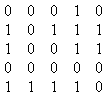
Pretraživanjem matrice susedstva na linearan način korišćenjem prethodne činjenice možemo da eliminišemo po jedan čvor.
Kada n − 1 pitanjem eliminišemo n − 1 čvorova, ostaće samo čvor kandidat. Za njega je potrebno utvrditi da li je zaista ponor, npr. kao u sledecem algoritmu.
Algoritam Ponor(A, n)
ulaz: A, n /* A je matrica susedstva grafa, n je broj čvorova u grafu*/
izlaz: kandidat
{
i = 0; j = 0; next = 1;
while (next < n)
{
if (A[i][ j] == 1)
{kandidat = j; // cvor i nije ponor
i = next;
}
else
{ kandidat = i; // cvor j nije ponor
j = next;
}
next = next + 1;
}
k = 0;
while (k < n)
{
if (A[kandidat][k] ==1) return -1; // nema ponora
if ((A[k][kandidat] == 0) && (kandidat!= k)) return -1; // nema ponora
k = k + 1;
}
return kandidat;
}
Pokažite da vremenska složenost algoritma jeste O(n).
T(n)= 3 /* i = 0; j = 0; next = 0;*/
+ n*c1 /* ciklus while (next < n) */
+ 1 /*k = 0;*/
+ n*c2 /* ciklus while (k < n) */
4. Implementirati BFS algoritam za obilazak grafa G=(V,E) koji je zadat matricom povezanosti (a[i][j]=1, ako postoji grana (i,j), inace a[i][j]=0) tako da ispise cvorove u redosledu obilaska.
IDEJA i podsecanje:
Kod BFS pretrage kada se stigne do nekog cvora x grafa G, najpre se obilaze njegovi neposeceni i neposredni susedi. Nakon toga se nastavlja BFS algoritam, tj. posecuju se svi neposeceni susedi iz prethodnog nivoa pretrage. Zbog toga se koristi FIFO (First InFirst Out) red.
SKICA resenja
Polazni cvor x grafa G
smesti se u niz red
poseti se
markira kao “posecen”
upisu se susedi cvora x u niz red (na kraj)
Poseti se sledeci cvor iz reda, markira kao posecen, njegovi neposeceni susedi se upisu u niz red
Ponavlja se korak 2 dok ima neposecenih cvorova u redu
void BFS(int
a[][50], int n)
/*a = matrica susedstva, n=broj cvorova grafa G
*/
{
int x; /* cvor grafa */
int m[50]; /*
m= niz markiranih cvorova garaf, vrednost clana m[x] ce postati 1,
kad se poseti cvor x, a inace 0 */
/*
inicijalizacija niza markiranih cvorova na 0, jer su na pocetku svi
cvorovi grafa neposeceni */
for (x=0; x<n; x++) m[x]=0;
/*
poseta grafa pocev od prvog neposecenog cvora */
for (x=0 ;x<n
;x++ )
if ( !m[x]) poseti (x, a, n, m)
}
void poseti(int
s, int a[][50], int n, int m[])
/*s = polazni cvor pretrage po
sirini, a = matrica susedstva, n = broj cvorova grafa, m = niz
posecenih cvorova*/
{
int i,k; /*brojaci u ciklusu
/
int v; /* cvor grafa */
int red [50]; /* niz cvorova
grafa poredjanih u poretku BFS pretrage */
/*inicijalizacije
niza m, red u odnosu na polazni cvor pretrage s*/
m[s]=1;
red[0]=s; k=1;
/*obilazak neposrednih suseda cvora s,
razlika od DFSa*/
for(i=0;i<k;i++)
{
s=red[i];
for(v=0;v<n;v++)
if( !m[v] && a[s][v])
{m[v]=1;
red[k++]=v; }
}
/*ispis BFS poretka*/
for(i=0;i<k;i++)
printf(“ %d “, red[i]);
}
5.
Implementirati algoritam povezan(a,n) kojim se u grafu
G=(V,E) sa n cvorova (gradova) proverava da li su svih
n cvorova povezani, tj. da li za ma koja dva grada postoji
put koji ih povezuje. Pretpostaviti da su veze izmedju gradova
zadate simetricnom matricom a dimenzije n*n takvom da
a[i][j]=1, ako postoji dvosmerna grana od cvora i do
cvora j, a[i][j]=0, ako ne postoji grana od
cvora i do cvora j.
Pokrenimo pretragu od grada 0 i obidjimo sve cvorove grafa i proverimo da li je broj clanova u nizu red jednak n.
void poseti(int
s=0, int a[][50], int n, int m[])
/*s = polazni cvor pretrage po
sirini, a = matrica susedstva, n = broj cvorova grafa, m = niz
posecenih cvorova*/
{
int i,k; /*brojaci u ciklusu
/
int v; /* cvor grafa */
int red [50]; /* niz cvorova
grafa poredjanih u poretku BFS pretrage */
/*inicijalizacije
niza m, red u odnosu na polazni cvor pretrage s*/
m[s]=1;
red[0]=s; k=1;
/*obilazak neposrednih suseda cvora s,
razlika od DFSa*/
for(i=0;i<k;i++)
{
s=red[i];
for(v=0;v<n;v++)
if( !m[v] && a[s][v])
{m[v]=1;
red[k++]=v; }
}
/*PROVERA!!!*/
return (k==n)}
6.
Implementirati algoritam postojiPut(g, a, n) kojim se
u grafu G=(V,E) sa n cvorova ispisuje na standardni izlaz do
kojih se cvorova moze doci polazeci od zadatog cvora g.
Pretpostaviti da su veze izmedju gradova zadate simetricnom matricom
a dimenzije n*n takvom da a[i][j]=1, ako postoji dvosmerna
grana od cvora i do cvora j, a[i][j]=0, ako ne postoji grana
od cvora i do cvora j.
Pozovemo algoritam poseti za s=g
Postavimo da mora biti red[0]=g, tj. polazni cvor pretrage je g
Na kraju u for ciklusu i=1..k-1, ispisemo clanove red[i]