Sravnivanje niski (trazenje uzorka/obrasca u tekstu) – naivni (elementarni) algoritam, KMP algoritam

Elementarni algoritam skaniranja se zasniva na skaniranju uzorka i teksta s leva u desno, i to tako što se poredi karakter po karakter (u parovima-karakter iz uzorka sa karakterom iz teksta). Pretpostavka je da se svaki dokument predstavlja kao jedna niska karaktera (s) koja ima ukupno n karaktera (slova, cifre, razni specijalni znaci, ...). Uzorak ili obrazac (p) takođe predstavlja nisku karaktera dužine m.

S= s₁ + s₂ + s₃ + ... + s_n n (i)

P= p₁ + p₂ + p₃ + ... + p_m m (j) n > m n >> m

Tipicno je tekst duži od uzorka (n > m) tačnije, tekst je mnogo duži od uzorka (n >> m). Elementarno sravnjivanje obrazaca prolazi kroz S i kroz P i polazi od krajnje leve pozicije.

/* Proverava da li string s sadrzi string p
Vraca poziciju na kojoj p pocinje, odnosno -1 ukoliko ga nema
*/
int Sravni_niske(char s[], char p[])
{
    int i, j;
  
/* Proveravamo da li p pocinje na svakoj poziciji i */
  for (i = 0; s[i]; i++)
         /*Poredimo p sa s pocevsi od znaka p[0] sve dok ne naidjemo na razliku */
      for (j = 0; s[i+j] == p[j]; j++)
        /* Nismo naisli na razliku, a ispitali smo sve karaktere niske p */
          if (p[j+1]=='\0') return i;

/* Nije nadjeno */
return -1;

}

Ovakva jedna strategija sravnjivanja je efikasna kada se obrazac sravni sa tekstom rano u procesu sravnjivanja. Kada se sravni pri kraju teksta broj karaktera raste. Ako su slični deo teksta i obrasci, ali se u poslednjem koraku otkrije neslaganje, nastupa najgori slučaj sravnjivanja. Primer za ovaj algoritam:

s₀ s₁ s₂ ... s_n-₄ s_n-₃s_n-₂ s_n_-1

Korak 1: s = a a a a a a ... a a b

ⁱ⁼⁰ p = a a b

√ √ x

Korak 2: a a b

ⁱ⁼¹ √ √ x

Korak 3: a a b

ⁱ⁼² √ √ x

...

Korak n - 3: a a b

^{i=
n -}⁴ √ √ x

Korak n -2: a a b

^{i=
n -}³ √ √ √

Ovo je jedan iskonstruisan slučaj, ali pokazuje koliki je broj poređenja potreban da bi se dobilo slaganje.

Broj poređenja je m*n (kada pomnožimo broj karaktera teksta sa brojem karaktera obrasca dobijamo koliko puta ponavljanje treba da se obavi).

Ovaj najgori slučaj se u praksi retko sreće jer se pretpostavka obori mnogo ranije (obrazac i tekst nisu toliko slični).

Poboljšani algoritam trazenja uzorka u tekstu – KMP algoritam

U prethodnom primeru postupak se zasniva na tome da se obrazac pomera za jednu poziciju u odnosu na tekst i za svaku poziciju u tekstu se pretpostavlja da može da bude početak obrasca. Ništa nije unapred poznato. Međutim, ako se obrazac koji se sravnjuje prvo analizira dobija se određeno saznanje o tekstu koje nam omogućava da se izbegne testiranje pretpostavke na svaku poziciju teksta. Te pozicije su strateški odabrane i na njima postoji teoretska mogućnost da se obrazac pronađe.

Tri čuvena informatičara i programera Knuth, Morris i Pratt su koncipirali algoritam koji se po njima zove KMP algoritam. Kasnije su ovaj algoritam doradili Aho i Corasick tako da može paralelno da ispituje više obrazaca.

Ovaj algoritam skanira tekst i obrazac isto s leva u desno, ali kada dođe do neslaganja obrazac se pomera za neki optimalan broj karaktera (a ne samo za 1 karakter).

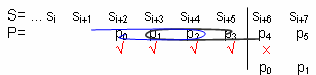
S= ... s_i s_i+1 s_i+2 s_i+3 s_i+4 s_i+5 s_i+6 s_i+7 ...

P= p₀ p₁ p₂ p₃ p₄ p₅

√ √ √ √ x

U sravnjivanju smo utvrdili da je karakter p₀ obrasca sravnjen sa karakterom s_i+2 teksta, karakter p₁ obrasca sravnjen sa karakterom s_i+3 teksta, ... Na poziciji s_i+6 smo utvrdili neslaganje. Kako se p₀ slaže sa s_i+2, p₁ sa s_i+3, itd, besmisleno je pomerati obrazac samo za jednu poziciju u odnosu na tekst jer ni tada ne može da dođe do slaganja. Ako u obrascu nema ponavljanja (tj. ako glava obrasca nije jednaka repu) odmah treba preći na neku sledeću poziciju:

Primer:

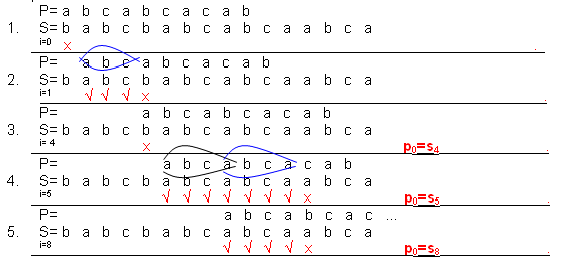
Počinjemo s leva u desno. Obrazac P se postavlja na prvi karakter teksta S. Kako je odmah došlo do neslaganja a!=b, obrazac P se pomera za jednu poziciju, i=1.

Sada poredimo drugi karakter teksta S[1] sa prvom pozicijom obrasca P[0], S[2] sa P[1], itd. U ovom koraku imamo tri poklapanja (ovaj deo teksta je sravnjen) - glava sravnjenog dela je jednaka repu sravnjenog dela jer nema ponavljanja, tako da se pozicije između 2 i 5 preskaču (pomeranje za 2, 3, 4 pozicije ne bi imalo smisla).

Prvi karakter obrasca P[0] se poredi sa petim karakterom teksta S[4]. Kako imamo neslaganje obrazac se pomera za jedno mesto.

U narednom koraku (i=5) imamo sravnjeni deo dužine 7. Sada se analizira da li u njemu ima neki deo koji odgovara početku ili kraju obrasca. Pošto postoji određeno slaganje, u sledećem koraku se obrazac pomera za 4 pozicije.

Da bismo utvrdili za koliko treba da pomerimo obrazac gledamo sravnjeni deo, da bismo utvrdili neku sličnost. Ako obrazac pomerimo za tri mesta, gde je bio sravnjen rep, biće sad sravnjena glava.

U petom koraku obrazac je prešao preko kraja teksta pa se sravnjivanje ne obavlja.

Kako se ispituje sam obrazac?

Kada se ispituje obrazac cilj je da se za svaku poziciju u obrascu utvrdi za koliko mesta treba pomeriti obrazac ako na nekoj poziciji dođe do neslaganja.

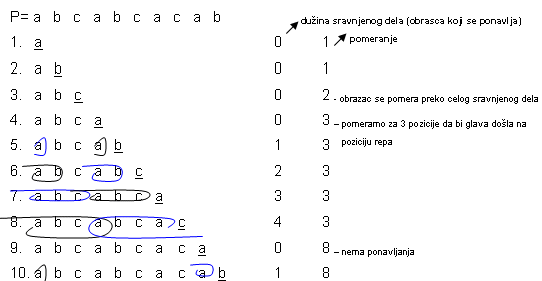
Ako već kod prvog koraka imamo neslaganje (ništa nije sravnjeno) obrazac se pomera za jedno mesto, itd.

Ako se obrazac ovako analizira (analizu radi program) za svaku poziciju na kojoj dođe do neslaganja tačno se zna za koliko treba pomeriti obrazac. Posebna prednost ovakve procedure je što ona radi sa tekstom idući s leva u desno i uniformno vrši pomeranje obrasca, a može i paralelno da proverava i više obrazaca.

Za razliku od prethodnog algoritma gde je u najgorem slučaju broj poređenja m*n, ovde je broj poređenja linearan tj. m+n.

Ovi algoritmi su posebno pogodni kada se radi sa specijalnom vrstom teksta (za utvrđivanje sličnosti DNK obrazaca)

KMP algoritam (C kôd)

void KMPtabela(char *p, int m, int kmpNext[]) {   /* kmpNext je tabela konstruisana za uzorak p koja se posle koristi u KMP algoritmu*/
   int i, j;  /* brojaci: i=indeks tabele kmpNext, j=pozicija smaknutog uzorka */

   i = 0;  
   j = kmpNext[0] = -1;
   while (i < m) {
      while (j > -1 && p[i] != p[j])
         j = kmpNext[j];  /* smanjivanje indeksa j */
      i++;
      j++;
      if (p[i] == p[j])
         kmpNext[i] = kmpNext[j];
      else
         kmpNext[i] = j;
   }
}


void KMP(char *p, int m, char *s, int n) {
   int i, j, kmpNext[PSIZE]; /*i=indeks uzorka, j=indeks teksta s, PSIZE = dimenzija uzorka p*/

   /* Izracunavanje KMP tabele za uzorak p */
   KMPtabela(p, m, kmpNext);

   /* Trazenje uzorka p u nisci s */
   i = j = 0;
   while (j < n) {
      while (i > -1 && p[i] != s[j])
         i = kmpNext[i]; /*pomeranje niske p udesno za i-kmpNext[i] */
      i++;
      j++;
      if (i >= m) {   /* USPEH: pronadjen podstring JEDNAK uzorku */
         STAMPAJ(j – i);  /* stampa se indeks pocetka prvog podstringa od s koji je jednak sa p */
         i = kmpNext[i];
      }
   }
}

PRIMER PRIMENE KMP algoritma na gore navedenom primeru: p=abcabcacab s=babcbabcabcaabca

m=10, n=16

kmpNext:

0	1	2	3	4	5	6	7	8	9	10
-1	0	0	-1	0	0	-1	4	-1	0	2

pokusaj 1:

babcbabcabcaabca

a.........

Pomeranje za: 1 (0-kmpNext[0])

pokusaj 2:

babcbabcabcaabca

ABCa......

Pomeranje za: 4 (3-kmpNext[3])

pokusaj 3:

babcbabcabcaabca

ABCABCAc..

Pomeranje za: 3 (7-kmpNext[7])

POKUSAJA: 3

Broj poredjenja karaktera: 13

ZADACI ZA VEZBU:

1. Traži se prva pojava uzorka atcacatcatca u tekstu gatcgatcacatcatcacgaaaaa.

(a) Izračunati brojeve pomeranja uzorka --- tabelu koja se koristi za algoritam KMP.

(b) Koliko puta se pomera uzorak do konačnog odgovora?

RESENJE:

n=24 m=12

kmpNext:

0	1	2	3	4	5	6	7	8	9	10	11	12
-1	0	0	-1	1	-1	0	0	-1	4	0	-1	4

pokusaj 1:

gatcgatcacatcatcacgaaaaa

a...........

Pomeranje za: 1 (0-kmpNext[0])

pokusaj 2:

gatcgatcacatcatcacgaaaaa

ATCa........

Pomeranje za: 4 (3-kmpNext[3])

pokusaj 3:

gatcgatcacatcatcacgaaaaa

ATCACATCATCA

Pomeranje za: 8 (12-kmpNext[12])

USPEH:

gatcgATCACATCATCAcgaaaaa

POKUSAJA: 3

Broj poredjenja karaktera: 17

2. Neka je tekst s=acabcacb , obrazac p=abacab

a) prikazati po koracima postupak sravnjivanja obrasca sa tekstom korišcenjem naivnog (elementarnog) algoritma

b) prikazati po koracima postupak sravnjivanja obrasca sa tekstom korišcenjem algoritma KMP.

RESENJE

b) n=8 m=6

kmpNext:

0	1	2	3	4	5	6
-1	0	-1	1	-1	0	2

pokusaj 1:

acabcacb

Ab....

Pomeranje za: 1 (1-kmpNext[1])

pokusaj 2:

acabcacb

a.....

Pomeranje za: 1 (0-kmpNext[0])

pokusaj 3:

acabcacb

ABa...

Pomeranje za: 3 (2-kmpNext[2])

POKUSAJA: 3

Broj poredjenja karaktera: 6

3. Modifikovati algoritam KMP tako da nalazi najveci prefiks uzorka P koji kao podstring postoji u tekstu S.

4. Obrazac prepreden se traži u tekstu kadsuprelaziliprekopreprekenasmejaseprepredeno

(a) Izracunati broj pozicija pomeranja obrasca za korišcenje Knut-Moris-Pratovog algoritma;

(b) Koliko puta se pomera obrazac do konacnog odgovora?

(Pratiti rad algoritma po koracima).

RESENJE:

n=46 m=9

kmpNext:

0	1	2	3	4	5	6	7	8	9
-1	0	0	-1	0	0	3	0	0	0

pokusaj 1: