Na potezu je IKS, ima tri polja na koja može igrati.
Problem: zadata je tablica za igru iks– oks na kojoj su već odigrani neki potezi. Treba utvrditi koji igrač ima strategiju koja vodi do pobede, te koji potez je optimalan potez igrača koji je na redu – na koje polje treba staviti svoju oznaku da bi pobedio ako je to moguće ili odigrao nerešeno ako je moguće
Neka je na potezu igrač “x”. Ako postoji način da on pobedi, toj situaciji se dodeli oznaka 1. Ako ne može pobediti, ali može igrati nerešeno, situacija se označava sa 0, a ako gubi kako god igrao situacija se označava sa -1
Slično, ako je na potezu “o”, situacija u kojoj on može pobediti se označava sa -1, kada može igrati najviše izjednačeno sa 0 i kada gubi sa 1
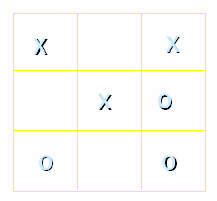
Primer: zadata je ovakva situacija:

Na
potezu je IKS, ima tri polja na koja može igrati.
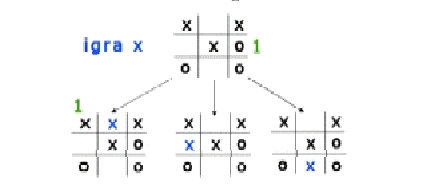
Dobije
se stablo situacija:
levo dete trivijalno ima oznaku 1, jer je pobeda za x.
Za ostalu decu se još ne znaju oznake, ali se zna da koren ima oznaku 1, jer je x na potezu i može pobediti
Ako x ne odigra svoj pobednički potez, moguće su ove situacije:
1. Desno dete je dobilo oznaku 0, jer je na potezu o i ako on odigra prvi potez, rezultat je nerešen, ako odigra drugi, pobeđuje x
2. Srednje dete dobija oznaku -1, jer zavisno od toga šta igra o, onda x gubi ili igra nerešeno
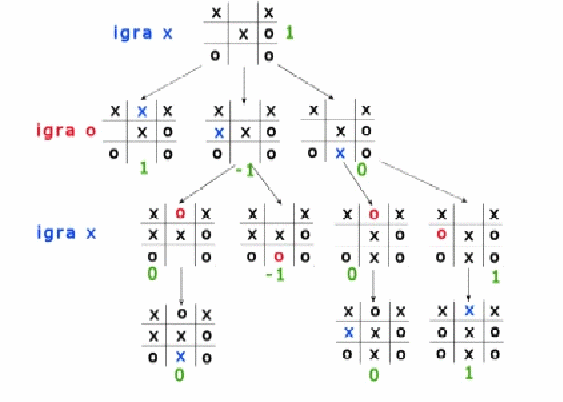
Iz
ovog je jasno da je oznaka svakog čvora u kojem je na potezu “o”
jednaka minimumu svih oznaka dece tog čvora i analogno ako je na
potezu “x” oznaka čvora je maksimum svih oznaka dece
čvora
Dakle,
algoritam rešavanja je: da bi se odredilo ko u zadatoj
situaciji pobeđuje treba kreirati stablo svih situacija
dostižljivih iz zadate situacije; koren stabla je zadata situacija, a
deca svakog čvora su situacije do kojih se dolazi u jednom
potezu iz tog čvora
Težina
utvrđivanja pobednika pada što je nivo čvora u
stablu veći
Listovi
stabla su trivijalne situacije – završetak igre
Za
utvrđivanje oznake u čvoru u kojem je na potezu “x”
potrebno je naći maksimum svih oznaka dece tog čvora;
za
određivanje oznake kad je na potezu “o” potrebno je
naći minimum svih oznaka dece tog čvora
Konstrukcija
takvog stabla se moze obaviti rekurzivnim algoritmom ciji pseudo-kod je:
tablica T– delimično popunjeno polje za igru
na_potezu – oznaka igrača koji je na potezu
izlazna promenljiva je:
igrati – optimalan potez kojeg igrač na potezu može odigrati i funkcija vraća oznaku čvora u stablu koji odgovara tablici T
int IKSOKS(tablica T, char na_potezu, potez *igrati) {
tablica dete;
potez ptemp;
int vrednost_deteta, temp;
if (T je list)
/* tablica je puna, funkcija pobednik() vraća 1 ako pobeđuje x, */ return pobednik(T);
/* 0 za nerešeno, -1 za pobedu o */
else {
if (na_potezu == ‘x’)
vrednost_deteta = -beskonačno;
else
vrednost_deteta = +beskonačno;
za svaki legalan potez move u tablici T radi {
if (na_potezu == ‘x’) {
dete = T + na mestu move je stavljen ‘x’;
temp = IKSOKS(dete, ‘o’, &ptemp);
if (temp > vrednost_deteta) {
vrednost_deteta = temp;
*igrati = move;
}
}
Konstruisati algoritam koji za datu sumu S i dati niz v koji sadrzi vrednosti novcanica pronalazi sva resenja za rasitnjavanja sume S. Pretpostaviti da svake novcanice ima proizvoljno mnogo.
U cemu je razlika ovog zadataka i zadatka resavanog tehnikom pohlepnog algoritma?
#include <stdio.h>
int s; /* novcani iznos koji treba razbiti */
int n; /* broj razlicitih novcanica */
int v[10]; /* vrednosti novcanica/apoena */
int x[10]; /* kolicina pojedinih apoena */
void pisi()
{ int i;
printf("\nRazmena: \n");
for(i=0; i<n; i++) printf("%d dinara:%d puta ", v[i],x[i]);
printf("\n");
}
void razmeni(int k, int s)
{
//k= redni broj apoena
//s = tekuca suma za rasitnjavanje
int i;
if(k>=n)
{ if(s==0) pisi();}
else
for(i=0; i<=s/v[k];i++)
{ x[k]=i;
razmeni(k+1, s -i*v[k]);
}
}
main()
{
int i;
printf("Unesite sumu i broj novcanica\n");
scanf("%d%d",&s,&n);
printf("\nUnesite vrednost za %d novcanica\n",n);
for(i=0; i<n;i++) scanf("%d",&v[i]);
razmeni(0,s);
}
3. Za n studenata i n studentkinja jednog fakulteta dati su podaci o ukupnom broju osvojenih poena na kvalifikacionom testu za kviz. Odrediti sto je moguce vise parova koji se mogu formirati unutar fakulteta i prijaviti za kviz parova ako svaki par cine po jedna studentkinja i jedan student i ako razlika u broju poena kod svkog para ne sme da predje dati broj p. 4. Dat je niz celih brojeva a[0]...a[n-1] i ceo broj S. Konstruisati algoritam koji postavlja operatore + - * / u izrazu (...(a[0]?a[1])?a[2])...)?a[n-1] tako da vrednost izraza bude S. Naci sva resenja.
Dat je pseudo-kod (bez f-je ispisa). Napisite je sami !!!
int s; /* vrednost izraza */
int n; /* broj operanada */
int jeste; /*indikator 0/1 da li vrednost izraza je s*/
int a[50]; /* vrednosti operanada izraza */
int z[50]; /* niz operatora izraza */
void racunaj(int k, int ts)
{
//k= redni broj primenjen operacije
//ts = tekuca suma izraza
if(k==n-1)
{ if(ts==s) {pisi(); jeste=1;} }
else
{ /*formiranje operatora unutar izraza */
z[k]='+'; racunaj(k+1, ts+a[k+1]);
z[k]='-'; racunaj(k+1, ts-a[k+1]);
z[k]='*'; racunaj(k+1, ts*a[k+1]);
if(a[k+1]!=0)
{z[k]='/'; racunaj(k+1, ts/a[k+1]); }
}
}
main()
{
int i;
printf("Unesite vrednost izraza i broj operanada izraza\n");
scanf("%d%d",&s,&n);
printf("\nUnesite vrednost za %d operanada\n",n);
for(i=0; i<n;i++) scanf("%d",&a[i]);
jeste=0;
racunaj(0,a[0]);
if (!jeste) printf("\nNema resenja\n");
}