Konstrukcija i analiza algoritama

I Konstrukcija algoritama

Algoritam koji zadovoljava rešenje formulisanog problema opisuje se

koracima
skupom ulaznih parametara
svojstvima koje moraju posedovati vrednosti na izlazu
skupom izlaznih vrednosti

Primer : Sortiranje

Input: a, N (a je niz od N celih brojeva ) a₁...a_n

Output: niz A sortiran u nerastućem poretku a₁ <= a₂ <= ... <= a_n

kôdiranje:

Zapis algoritama

shemom
pseudo-kôdom
programskim jezikom
prirodnim jezikom

kôdiranje programskim jezikom:

for(j=0; j<N-1; j++)
  for(k=j+1; k<N; k++)
if( A[j]>A[k] )
   {
     int rezerva;
     rezerva=A[j];
     A[j]=A[k];
     A[k]=rezerva;
    }

Ciljevi tokom ovog semestra: konstruisati algoritam koji je KOREKTAN i EFIKASAN.

II Korektnost

Potrebno je za svaki algoritam pokazati da uvek kao rezultat vraća očekivani izlaz za sve dozvoljene ulazne parametre formulisanog problema.

Na primer:
kod sortiranja izlaz mora biti neopadajući poredak niza A, čak i ako niz A
(1) već jeste sortiran, ili
(2) sadrži elemente koji se ponavljaju..

Šta mislite, nad koliko test primera je potrebno propustiti program da bi proverili da je on korektan? Da li je dovoljno 2, 10, 1000 test primera?

Primeri konstrukcije sa algoritama dokazom korektnosti

III Efikasnost

Da li je dovoljno da naš program radi korektno? Da li je potrebno da bude i efikasan?

Efikasnost se meri potrošnjom računarskih resursa pri izvršavanjem programa, a najznačajniji su vreme i prostor

Vreme izvršavanja

zavisi od sledećih faktora:

skupa mašinskih instrukcija računara na kom se algoritam izvršava, vremena njihovog trajanja u ciklusima, kao i trajanja jednog ciklusa

Na primer: i=i+1; i++; i+=1;

kvaliteta mašinskog kôda generisanog od strane prevodioca

Na primer: a=3; b=a+3; ILI a=3; b=6;

ulaznih podataka

vremenske složenosti algoritma

Faktori 1 i 2 zavise od konkretnog računara i prevodioca i ne odražavaju suštinu algoritma.

Vremenska složenost algoritama (svojstvo 4) se meri u odnosu na prebrojani broj upotrebljenih koraka.

IV RAM model

Analiza performansi algoritama u računarstvu se može odvijati i nezavisno od analize performansi hardvera ili konkretnog programskog jezika, iako kompletna analiza pretenduje da diskutuje i o uticaju tih parametara.

Za potrebe ALGORITMIKE se pri konstrukciji algoritama i diskusiji o njihovim osobinama koristi RAM model:

svaka "elementarna" operacija (+, -, =, if, višestruka selekcija) traje tačno 1 korak.

Petlje i pozivi potprograma nisu elementarne operacije i zavisne su od veličine podataka sa kojima rade i od sopstvenih podkoraka. Npr. sortiranje nije 1-koračna operacija.

Pristup memoriji se može uzeti za 1-koračnu operaciju.

Gore navedene pretpostavke važe sve dok se ne kaže drukčije.

V Najbolji, najgori i prosečan slučaj

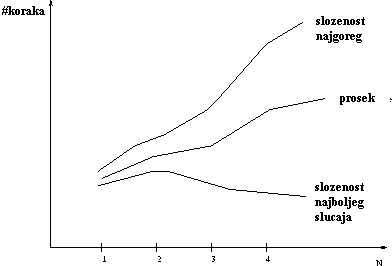
Složenost najgoreg slučaja algoritma jeste funkcija definisana u odnosu na najveći broj potrebnih koraka za obradu ulaza dimenzije n.

Složenost najboljeg slučaja algoritma jeste funkcija definisana u odnosu na najmanji broj potrebnih koraka za obradu ulaza dimenzije n.

Složenost prosečnog slučaja algoritma jeste funkcija definisana u odnosu na prosečni broj potrebnih koraka za obradu ulaza dimenzije n.

PRIMER 7: Sortiranje umetanjem

Niz od n elemenata se može sortirati tako što se pretpostavi da se n-1 elemenata mogu sortirati, a potom se umetne n-ti element na mesto koje mu pripada, tako što se pregleda n-1 sortiranih elemenata sve dok se ne pronađe odgovarajuđa pozicija za umetanje.

Dakle, počne se sa praznom listom , a potom se, umeću novi elementi na adekvatna mesta u nizu:

a₁<=a₂<=...<=a_k| a_k+1...a_n

U svakoj iteraciji, umetnuti element napušta sortiranu listu, i nakon do n umetanja pronalaze se korektne pozicije, te je otuda algoritam korektan.
Ali, koliko je on EFIKASAN?

Potrebno je uočiti koliko predsortiranost ulaza utiče na broj koraka, tj. slučaj već sortiranog niza u zahtevanom poretku i slučaj niza u obrnutom poretku i slučaj nesortiranog niza.

Precizna analiza algoritma

Prebrojmo koliko puta će se izvršiti svaka linija pseudokôda

Br linije InsertionSort(A) #Inst. #Izvrš.

1 for (j=1; j<n; j++) c1 1+n*1 +n-1

2 {pom=A[j]; c2 n-1

3 /* smesti A[j] unutar A[0..j-1] */ c3=0 /

4 i=j-1; c4 n-1

5 while (i>=0 && A[i]>pom) c5 t_j

6 {A[i+1]= A[i]; c6

7 i = i-1; } c7

8 A[i+1]=pom; } c8 n-1

for ciklus ima (n-1) iteracija

Unutar for ciklusa se dodela"pom=A[j]" obavi n-1 puta.

Koraci 5, 6, 7:

Za svako j, neka t_j je broj ponavljanja provere (i>=0 && A[i]>pom),
To je, zapravo, 1+ broj elemenata koji se moraju pomeriti udesno da bi se umetnuo element sa rednim brojem j, (element pom=a[j-1]).

Korak 5 se izvrsava puta.

Korak 6: .

Ukupno vreme izvrsavanja algoritma je:

gde t_j su zavisni od ulaznih parametara (zbog relacije poređenja)

Najbolji slučaj

Ako niz jeste vec sortiran u zahtevanom poretku, onda su svi t_j jednaki 1.

Otuda je vreme najboljeg slučaja

gde C i D su konstante, tj. složenost je O(n)

Najgori slučaj

Ako je niz sortiran u obrnutom poretku, potrebno je pomeriti sve vec sortirane elemente, tako da

, a korak 5 se izvrsava za

Dakle, n-ti element se upoređuje sa svih prethodnih n-1 brojeva. U najgorem slučaju se u n-tom koraku premesta n-1 brojeva, te je i broj premestanja/kopiranja O(n²)

Dakle, ukupan broj uporedjivanje moze biti 1+2+...+n-1=n(n-1)/2=O(n²)

Inače, sortiranje umetanjem se moze poboljsati binarnom pretragom (ali ona ne utice na smanjenje broja kopiranja) ili ukrštanjem sa sortiranjem izborom.

Podsećanje na gradivo iz prethodne godine

Jelena Hadži-Purić

Algoritmi i strukture podataka

e-mail: Jelena Hadži-Purić

Br linije	InsertionSort(A)	#Inst.	#Izvrš.
1	for (j=1; j<n; j++)	c1	1+n*1 +n-1
2	{pom=A[j];	c2	n-1
3	/* smesti A[j] unutar A[0..j-1] */	c3=0	/
4	i=j-1;	c4	n-1
5	while (i>=0 && A[i]>pom)	c5	t_j
6	{A[i+1]= A[i];	c6
7	i = i-1; }	c7
8	A[i+1]=pom; }	c8	n-1