Dinamičko programiranje (DP) je nastalo kao način rešavanja jedne klase algoritamskih problema, u kojima se traži optimalno rešenje, odnosno rešenje koje maksimizira ili minimizira neku zadatu veličinu. Kasnije se naziv preneo na širu klasu problema koji se rešavaju u osnovi istom idejom, a to je rešavanje manjih problema istog tipa i njihovo kombinovanje radi dobijanja rešenja polaznog, većeg problema. DP je tehnika oblikovanja rešenja koja rastavlja složen problem na manje složene potprobleme/korake. Za DP važno je usvojiti specifičan način razmišljanja pomoću kog treba: 1. pronaći sva stanja Pri rešavanju probleme upotrebom DP-a, potrebno je rastaviti problem na stanja. Stanje je rešenje nekog malog dela problema. 2. Na temelju prethodno izračunatih stanja, izračunati novo stanje (moramo znati relaciju) 3. Dinamike (algoritmi koji koriste DP) izračunavaju stanja takvim redom, tako da se niti jedno stanje ne izračunava dva puta. 4. Poznavati početna stanja Sama reč programiranje u terminu dinamičko programiranje se kao i u linearnom programiranju odnosi na popunjavanje tabele pri rešavanju problema, a ne na upotrebu programskog jezika ili računara. Tehnike optimizacije koje koriste dinamičko programiranje bile su poznate i pre II svetskog rata, ali se tvorcem metode smtra profesor Richard Belman, koji je sredinom pedesetih godina proučavao problem tako što je proučavao hijerarhiju podproblema sadržanih u glavnom problemu i rešavanje počinjao od najjednostavnijih. Algoritmi iz prakse koji koriste dinamičko programiranje 1. Cocke-Younger-Kasami (CYK) algoritam - određuje da li i kako zadati string se može generisati iz zadate kontekst-slobodne gramatike 2. transpoziciona tabela za igranje šaha na računaru, račinanje pozicija premeštanja i napada 3. Viterbi algoritam, nalaženje najverovatnije sekvence za neko skriveno stanje, npr. šema za korekciju grešaka u digitalnim komunikacionim linijama u kojima se pojavljuju i šumovi; 4. Floyd algoritam za nalaženje najkraćih puteva u grafu
Zadatak 1
Demonstrirati proces rešavanja problema maksimalne vrednosti ranca za
veličinu ranca K = 12, veličine predmeta k₁ = 9, k₂ = 7, k₃ = 4,
k₄ = 10, k₅ = 3 i vrednosti predmeta v₁ = 1, v₂ = 2, v₃ = 3,
v₄ = 4, v₅ = 5 gde je moguće da se predmeti ponavaljaju.
Rešenje: matrica C/1:
0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
1 | | | | | | | | | | | | |
k₁ = 9 1/0 | | | | | | | | | 1/1 | | | |
k₂ = 7 1/0 | | | | | | | 2/1 | | 1/0 | | | |
k₃ = 4 1/0 | | | | 3/1 | | | 2/0 | 6/2 | 1/0 | | 5/1 | 9/3 |
k₄ = 10 1/0 | | | | 3/0 | | | 2/0 | 6/0 | 1/0 | 4/1 | 5/0 | 9/0 |
k₅ = 3 1/0 | | | 5/1 | 3/0 | |10/2 | 8/1 | 6/0 |15/3 |13/2 |11/1 |20/4 |Zaključak: maksimalno popunjavanje ranca veličine 12 postiže se sa četiri predmeta k5 .
Zadatak 2
Neka je dat skup prirodnih brojeva {x₁, x₂ , …, xₙ} i neka je S njihova suma.
Konstruisati algoritam složenosti O(nS) koji razlaže ovaj skup u dva
disjunktna podskupa sa jednakim sumama elemenata, ili utvrdjuje da takvo
razlaganje nije moguće.
Uputstvo: Svaki od podskupova treba da ima sumu S/2, pa možemo primeniti
algoritam Ranac na skup vrednosti {x₁, x₂, …, xₙ} i veličinu ranca
S/2. On će biti složenosti O(nS/2) = O(nS).
Zadatak 3
Dato je n pravougaonika koji su numerisani brojevima od 1 do n.
Postavićemo svaki od tih pravougaonika na osu OX u smeru sleva nadesno
redom poštujući redosled numeracije pravougaonika. Svaki pravougaonik
je postavljen na osu OX svojom dužom ili kraćom stranicom. Potrebno
je izračunati dužinu gornjeg dela konture tj. obim konture bez dužine leve,
desne i donje ivice. Napisati program koji će naći maksimalnu moguću dužinu
gornjeg dela konture.
Sa standardnog ulaza se učitava vrednost za n (0 < n < 1000), a potom
se iz svake od n linija učitavaju po dva cela broja aᵢ i bᵢ koji
predstavljaju dužine stranica i-tog pravougaonika (0 < aᵢ < bᵢ < 1000) za
svako i = 1, 2, …, n.
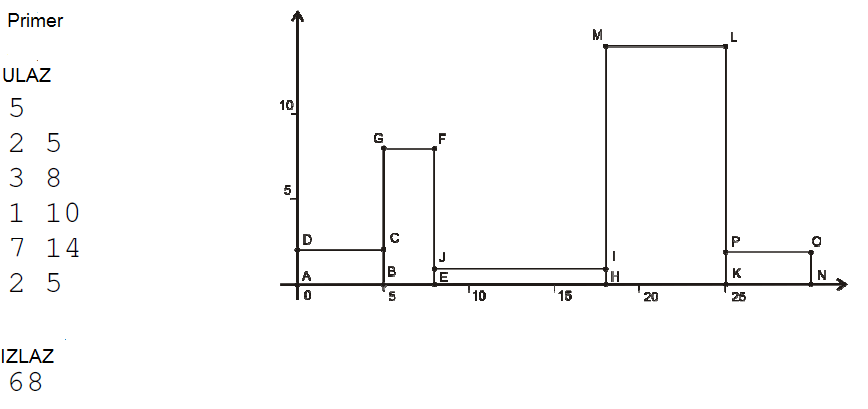 Objasnjenje primera: Na slici je predstavljen raspored pravougonika za koji se dobija maksimalna duzina gornjeg dela konture.
Gornji deo konture se sastoji od duzi DC, CG, GF, FJ, JI, IM, ML,LP, PO. Ukupna duzina je 5 + 6 + 3 + 7 + 10 + 13 + 7 + 12 + 5 = 68.
Objasnjenje primera: Na slici je predstavljen raspored pravougonika za koji se dobija maksimalna duzina gornjeg dela konture.
Gornji deo konture se sastoji od duzi DC, CG, GF, FJ, JI, IM, ML,LP, PO. Ukupna duzina je 5 + 6 + 3 + 7 + 10 + 13 + 7 + 12 + 5 = 68.
Rešenje: Dinamičko programiranje koje koristi induktivni pristup:
Uputstvo:
Označimo sa f(i) maksimalnu dužinu gornje konture za prvih
i pravougaonika takvih da je poslednji pravougaonik medju njima smešten
na osu OX svojom kraćom stranicom, a sa g(i) maksimalnu dužinu gornje
konture za prvih i pravougaonika tavkih da je poslednji pravougaonik
smešten na osu OX svojom dužom stranom.
Jasno je da važi: f(1) = a₁ i g(1) = b₁.
Važi:
f(i + 1) = aᵢ₊₁ + max { f(i) + |bᵢ − bᵢ₊₁|, g(i) + |aᵢ − bᵢ₊₁| }
g(i + 1) = bᵢ₊₁ + max { f(i) + |bᵢ − aᵢ₊₁|, g(i) + |aᵢ − aᵢ₊₁| }Indukcijom dobijamo vrednosti f(n) i g(n) i konačno rešenje biće veći od
ova dva broja.
#include<stdio.h>
#include<math.h>
#define N 1000
int max(int a, int b){
return (a >= b) ? a : b;
}
int main(){
int a[N], b[N];
int f[N], g[N];
int n, i;
scanf("%d",&n);
for (i = 0; i < n; i++) {
scanf("%d %d", &a[i], &b[i]);
}
f[0] = a[0];
g[0] = b[0];
for (i = 1; i < n; i++){
f[i] = a[i] + max(f[i - 1] + abs(b[i - 1] - b[i]),
g[i - 1] + abs(a[i - 1] - b[i]));
g[i] = b[i] + max(f[i - 1] + abs(b[i - 1] - a[i]),
g[i - 1] + abs(a[i - 1] - a[i]));
}
printf("%d", max(f[n - 1], g[n-1]));
}Zadatak 4
Dat je niz od n reči, dužina l₁, l₂, …, ln, koji želimo da lepo otkucamo.
Svaki red može da sadrži najviše P karaktera, tekst treba da bude poravnat
ulevo i ne sme biti preloma reči izmedju redova. Ako red sadrži reči
počev od i-te zaključno sa j-tom, uključujući i jednu i drugu, tada je
broj praznih mesta na kraju reda:
j
s = P - Σ lₖ - (j - i)
k=iŽelimo da ispišemo tekst tako da izbegnemo velike prazne prostore na kraju redova; formalno, želimo da minimizujemo sumu po svim redovima kvadrata broja praznih mesta na kraju reda. Dati efikasan algoritam za ovaj problem i odrediti njegovo vreme izvršavanja.
Uputstvo: Problem ćemo rešiti dinačkim programiranjem. U nameri da
optimalno otkucamo reči 1, 2, …, j, moramo prvo optimalno da otkucamo
reči 1, 2, …, i za neko i < j, a da onda preostale reči i + 1, …, j otkucamo
u poslednjem redu.
Označimo sa A[j] optimalnu cenu koju možemo da postignemo štampanjem
reči: 1, 2, …, j. Možemo rekurzivno da izrazimo A[j] kao:
A[j] = min A[i] + (P - (T[j] - T[i]))², i<j:T[j]−T[i]<Pgde je
j
T[j] = Σ lᵢ + (j - 1)
i=1jer za prvih j reči treba izmedju njih postaviti j − 1 belinu.
(P − (T[j] − T[i]))² označava kvadrat broja praznih mesta u poslednjem redu.
Moguće je izračunati unapred niz vrednosti T[j], j = 1..n u vremenu O(n).
Nakon toga, koristeći tehniku dinamičkog programiranja, računamo redom
svaku od vrednosti A[j]. Za svaku od vrednosti potrebno je, u najgorem
slučaju, pogledati O(n) prethodno izračunatih vrednosti, te je potrebno
vreme O(n), a pošto je potrebno izračunati vrednosti n elemenata niza A,
ukupno vreme izvršavanja je O(n²).
Moguće je izvršiti i rekonstrukciju samog rešenja, tj pozicija gde treba preći u novi red, održavanjem pokazivača unazad, što je česta praksa u dinamičkom programiranju.
Zadatak 5
Neka je x₁, x₂, …, xₙ niz realnih (ne obavezno pozitivnih) brojeva različitih
od nule. Konstruisati algoritam složenosti O(n) za odredjivanje
proizvoda podniza xᵢ, xᵢ₊₁, …, xⱼ sa najvećim mogućim proizvodom, 1 ≤ i ≤ j ≤ n.
Proizvod praznog niza je po definiciji jednak 1.
(glava 4.8) Nalaženje maksimalnog uzastopnog podniza: podsećanje: http://poincare.matf.bg.ac.rs/~jelenagr/pr/v2.htm
Uputstvo: Rešiti prvo za cele brojeve, pa uopštiti na realne. Za razliku od sabiranja, ovde zbog negativnih brojeva moramo da pamtimo dva medju-proizvoda, jedan maksimalni, jedan minimalni. Ako smo naisli na negativan broj, ono sto je do sada bio maksimalni proizvod ce postati minimalni kad se pomnozi trenutnom vrednoscu, i obratno.