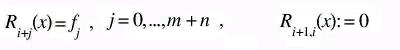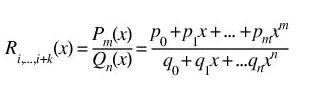
where Ri,...,i+k(x) is determined by (m+n+1) interpolation conditions
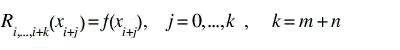
Dividing numerator and denominator with one of coefficients pi or qi, number of unknown parameters is reduced for one, and their number is (m+n+1). Unknown parameters are uniquely determined by interpolation conditions. Therefore, rational interpolation is determined by giving ordered pair (m, n) and array of real numbers fj ( j=0,...,m+n ).
If we need to calculate near value of function f(x) for given x with rational interpolation method, it is not adequate, especially for great values of m and n, for finding R(x). It is better, if m=n, to use algorithm of Neville type: