Prilikom računarske obrade svi geometrijski objekti se predstavljaju analitički: brojevima (koordinatama, koeficijentima i slično). Pretpostavlja se da je čitalac upoznat sa osnovama analitičke geometrije. Ipak, u nastavku ćemo rezimirati neke osnovne pojmove korisne prilikom konstrukcije geometrijskih algoritama, pri čemu ćemo većinu operacija zasnovati na vektorima i operacijama sa njima (alternativno, u tradicionalnoj analitičkoj geometriji se geometrijski objekti obično predstavljaju implicitnim jednačinama). Bavićemo se pitanjima poput izračunavanja rastojanja između dve tačke, ispitivanja kolinearnosti tri tačke ili izračunavanja presečne tačke dveju duži. Sve ove operacije mogu se izvesti algoritmima konstantne vremenske složenosti, korišćenjem osnovnih aritmetičkih operacija. Pretpostavljamo i da se različite elementarne funkcije (kvadratni koren, trigonometrijske funkcije i slično) mogu izračunati za konstantno vreme. Međutim, pošto je izračunavanje tih funkcija sporije od elementarnih računskih operacija, treba ih izbegavati kada god je to moguće.
Osnovni geometrijski objekti su tačke i većina drugih objekata se predstavlja pomoću tačaka. Prava je najčešće predstavljena parom različitih tačaka \(P\) i \(Q\) koje joj pripadaju. Duž se najčešće zadaje parom tačaka \(P\) i \(Q\) koje predstavljaju krajeve te duži, i označavaćemo je sa \(PQ\).
Tačke se u računaru najčešće predstavljaju svojim Dekartovim koordinatama. Tačke u ravni se predstavljaju parom Dekartovih koordinata \((x, y)\), a tačke u trodimenzionom prostoru trojkom Dekartovih koordinata \((x, y, z)\). U zavisnosti od primene, koordinate su najčešće ili celobrojne ili realne (u računaru najčešće predstavljene brojevima u pokretnom zarezu).
Tačke se mogu predstaviti ili strukturnim tipom ili ugrađenim tipom za predstavljanje uređenih \(n\)-torki (tj. parova ako su tačke u ravni). Na primer, tačke u ravni sa celobrojnim koordinatama mogu se predstaviti na bilo koji od sledeća dva načina.
struct Tacka {
int x, y;
};typedef pair<int, int> Tacka;Naravno, umesto tipa int mogu se koristiti i drugi tipovi za predstavljanje koordinata (npr. long long, float, double itd.).
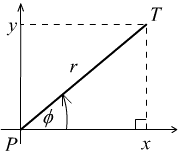
U nekim algoritmima je pogodnija reprezentacija tačaka pomoću njihovih polarnih koordinata. Zbog toga je za date Dekartove koordinate \(x\) i \(y\) tačke \(A\) ponekad potrebno odrediti njene polarne koordinate: rastojanje \(r\) od koordinatnog početka \(O\) i ugao \(\phi\) koji duž \(OA\) zahvata sa pozitivnim delom \(x\) ose i, obratno, na osnovu polarnih koordinata odrediti Dekartove. Ugao se često razmatra kao orijentisani ugao iz intervala \((-\pi, \pi]\) ili \([0, 2\pi)\), gde ugao \(0\) predstavlja pozitivan smer \(x\) ose i ugao raste u pozitivnom matematičkom smeru.

Da bismo transformisali polarne koordinate u Dekartove, možemo iskoristiti sledeću vezu (slika 1):
\[\begin{eqnarray*} x&=&r\cos \phi \\ y&=&r\sin\phi \end{eqnarray*}\]
Za transformaciju Dekartovih koordinata u polarne u većini slučajeva možemo iskoristiti naredne jednačine:
\[\begin{eqnarray*} r&=&\sqrt{x^2+y^2}\\ \phi&=&\arctan \frac{y}{x} \end{eqnarray*}\]
Prethodne formule nisu uvek ispravne, jer vrednost \(\arctan \frac{y}{x}\) nije definisana za \(x=0\), tj. za tačke na \(y\)-osi. Takođe, vrednost funkcije \(\arctan\) je uvek u intervalu \((-\pi/2, \pi/2]\), a ne u intervalu \((-\pi, \pi]\) (ili \([0, 2\pi)\)), kako bismo želeli. Zbog toga se umesto funkcije \(\mathrm{arctan}\) definiše i koristi funkcija \(\mathrm{arctan2}\), koja ima dva argumenta: \(y\) i \(x\) koordinatu tačke čiji se polarni ugao izračunava kao \(\phi = \mathrm{arctan2}(y, x)\) (obratiti pažnju na redosled argumenata). Ova funkcija je direktno podržana u većini programskih jezika (pod nazivom atan2) i vraća ugao iz intervala \((-\pi, \pi]\).
\[\begin{align*} \mathrm{arctan2}(y, x) = \begin{cases} \arctan\left(\frac{y}{x}\right) & \text{za } x > 0 \\ \arctan\left(\frac{y}{x}\right) + \pi & \text{za } x < 0 \text{ i } y \geq 0 \\ \arctan\left(\frac{y}{x}\right) - \pi & \text{za } x < 0 \text{ i } y < 0 \\ +\frac{\pi}{2} & \text{za } x = 0 \text{ i } y > 0 \\ -\frac{\pi}{2} & \text{za } x = 0 \text{ i } y < 0 \\ \text{nedefinisano} & \text{za } x = 0 \text{ i } y = 0 \\ \end{cases} \end{align*}\]
Pored tačaka, osnovni pojam analitičke geometrije predstavljaju vektori. Vektori se predstavljaju uređenim parovima tačaka tj. usmerenim dužima. Usmerena duž \((A, B)\), koja ima početnu tačku \(A\) i krajnju tačku \(B\) određuje vektor \(\overrightarrow{AB}\). Svi druge usmerene duži tj. parovi tačaka \((A', B')\) takvih da postoji translacija kojom se par \((A, B)\) preslikava na par \((A', B')\) određuju isti vektor (vektori su, dakle, klase ekvivalencije usmerenih duži). Ako su početna i krajnja tačka vektora jednake, one određuju tzv. nula-vektor (govorićemo i da je u pitanju vektor jednak nuli).
Vektori se mogu sabirati i skalirati (množiti brojem, tj. skalarom). Izraz \(\overrightarrow{a} + \overrightarrow{b}\) označava zbir vektora \(\overrightarrow{a}\) i \(\overrightarrow{b}\), dok izraz \(k\cdot \overrightarrow{a}\) označava skaliranje vektora \(\overrightarrow{a}\) skalarom \(k\). Vektori se mogu i oduzimati. Razlika vektora \(\overrightarrow{a}\) i \(\overrightarrow{b}\) se definiše kao \(\overrightarrow{a} - \overrightarrow{b} = \overrightarrow{a} + (-1)\cdot \overrightarrow{b}\). Sabiranje i skaliranje imaju svoju geometrijsku interpretaciju (slika 2).
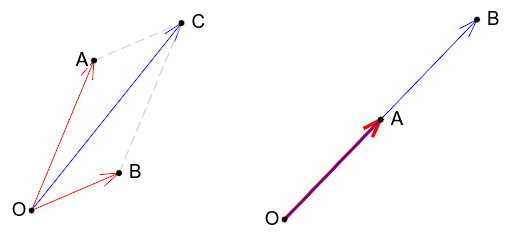
Naredna dva apleta prikazuju geometrijsku interpretaciju sabiranja i skaliranja vektora.
Vektori se najčešće predstavljaju analitički, svojim Dekartovim koordinatama (parom koordinata za vektore u ravni i trojkom koordinata za vektore u prostoru). Svaki vektor u ravni se može jednoznačno izraziti kao linearna kombinacija proizvoljna dva nekolinearna jedinična vektora \(\overrightarrow{i}\) i \(\overrightarrow{j}\), tj. za svaki vektor \(\overrightarrow{a}\) postoje brojevi \(x\) i \(y\) takvi da je \(\overrightarrow{a} = x\cdot \overrightarrow{i} + y \cdot \overrightarrow{j}\). Brojevi \((x, y)\) predstavljaju koordinate vektora \(\overrightarrow{a}\). Dekartov koordinatni sistem je određen međusobno normalnim jediničnim vektorima \(\overrightarrow{i}\) i \(\overrightarrow{j}\) i koordinatnim početkom \(O\) i u nastavku ćemo uvek podrazumevati da radimo sa ovakvim koordinatnim sistemom.
Sabiranje i skaliranje vektora se lako izražavaju analitički. Zbir vektora \(\overrightarrow{a} = (a_x, a_y)\) i \(\overrightarrow{b} = (b_x, b_y)\) je vektor \(\overrightarrow{a} + \overrightarrow{b} = (a_x + b_x, a_y + b_y)\). Proizvod vektora \(\overrightarrow{a} = (a_x, a_y)\) i skalara \(k\) je vektor \(k\cdot \overrightarrow{a} = (ka_x, ka_y)\). Intenzitet vektora \(\overrightarrow{a}\) čije su koordinate \((x, y)\) se izračunava Pitagorinom teoremom \(|\overrightarrow{a}| = \sqrt{x^2+y^2}\).
Vektor u ravni se u jeziku C++ može predstaviti sledećom strukturom.
struct Vektor {
double x, y;
};Koordinate bilo koje tačke \(A\) su zapravo koordinate vektora \(\overrightarrow{OA}\).
Sabiranjem tačke i vektora tačka se translira za dati vektor. Ako su poznate koordinate tačke \(A\) i vektora \(\overrightarrow{AB}\), njihovim sabiranjem dobijaju se koordinate tačke \(B\). Zaista, važi \(\overrightarrow{OB} = \overrightarrow{OA} + \overrightarrow{AB}\). Ovo ćemo kraće zapisivati kao: \(B = A + \overrightarrow{AB}\).
Oduzimanjem tačaka dobija se vektor koji ih spaja. Ako su poznate koordinate početne i krajnje tačke vektora \(\overrightarrow{AB}\), tada se koordinate vektora \(\overrightarrow{AB}\) mogu izračunati oduzimanjem koordinata tačke \(A\) od koordinata tačke \(B\). Zaista, važi \(\overrightarrow{AB} = \overrightarrow{OB} - \overrightarrow{OA}\). Ovo ćemo kraće zapisivati kao: \(\overrightarrow{AB} = B - A\).
U aplikaciji za crtanje treba implementirati funkcionalnost iscrtavanja strelice. Strelica ima svoje telo (duž \(AB\)) i vrh (koji se crta pomoću dve kraće duži \(BM\) i \(BN\)). Ako su poznate koordinate krajnjih tačaka tela strelice \(AB\), dužina duži \(|BM|=|BN|=d\) kojima se crta vrh i konveksan ugao \(\alpha\) koji zaklapaju duži na vrhu strelice, odrediti koordinate krajnjih tačaka duži kojima se vrh predstavlja.
U prvoj liniji standardnog ulaza se nalaze koordinate tačke \(A\) (dva realna broja), u drugoj liniji koordinate tačke \(B\) (različite od tačke \(A\)), u trećoj dužina \(d\) duži na vrhu strelice (pozitivan realan broj) i u četvrtoj konveksan ugao \(\alpha\) između duži na vrhu strelice (u stepenima).
Na standardni izlaz ispisati koordinate krajnjih tačaka \(M\) i \(N\) duži pri vrhu strelice (različite od tačke \(B\)).
0 0 4 4 1 90
4 3 3 4
Neka su tačke \(A\) i \(B\) krajnje tačke tela strelice, a \(P\) i \(Q\) krajnje tačke duži na vrhu strelice (kako je prikazano na slici.

Neka je tačka \(M\) presečna tačka duži \(AB\) i \(PQ\). Koordinate tačaka \(P\) i \(Q\) možemo odrediti kao \(P = M + \overrightarrow{MP}\) i \(Q = M + \overrightarrow{MQ}\). Koordinate tačke \(M\) možemo odrediti kao \(M = B + \overrightarrow{BM}\).
Pravac vektora \(\overrightarrow{BM}\) je isti kao pravac vektora \(\overrightarrow{BA} = A - B\). Zato je \(\overrightarrow{BM} = |BM| \cdot \frac{\overrightarrow{BA}}{|BA|}\).
Intenzitet \(|BM|\) možemo odrediti korišćenjem elementarne trigonometrije. Važi da je ugao \(\angle PBQ = \alpha\), pa je ugao \(\angle PBM = \alpha/2\). Trougao \(PMB\) je pravougli, pa važi da je \(\sin(\alpha/2) = |MP| / |PB|\) i \(\cos(\alpha/2) = |BM| / |PB|\). Dužina \(|PB|\) je poznata i jednaka je \(d\), pa je \(|MP| = |MQ| = d\sin(\alpha/2)\) i \(|BM| = d\cos(\alpha/2)\).
Ostaje još da odredimo vektore \(\overrightarrow{MP}\) i \(\overrightarrow{MQ}\). Njihove intenizitete znamo (na osnovu prethodnog trigonometrijskog izvođenja) i ostaje da im odredimo pravac. Pošto su oni upravni na vektor \(\overrightarrow{BA}\), njihov pravac se može dobiti rotiranjem vektora \(\overrightarrow{BA}\) za \(90\) stepeni u jednom ili drugom smeru. U opštem slučaju važi da ako su koordinate vektora \((x, y)\), rotiranjem za 90 stepeni dobijaju se vektori čije su koordinate \((-y, x)\) i \((y, -x)\).
// vektor BA
double BAx = Ax - Bx, BAy = Ay - By;
// duzina vektora BA
double BA = sqrt(BAx*BAx + BAy*BAy);
// ugao alpha/2 u radijanima
double alpha2 = (alpha/2) / 180 * M_PI;
// duzina vektora BM
double BM = d * cos(alpha2);
// duzina vektora MP i MQ
double MP = d * cos(alpha2), MQ = MP;
// vektor BM
double BMx = BM * BAx / BA, BMy = BM * BAy / BA;
// tacka M
double Mx = Bx + BMx, My = By + BMy;
// vektor MP
double MPx = MP * (-BAy / BA), MPy = MP * (BAx / BA);
// tacka P
double Px = Mx + MPx, Py = My + MPy;
// vektor MQ
double MQx = MQ * (BAy / BA), MQy = MQ * (-BAx / BA);
// tacka Q
double Qx = Mx + MQx, Qy = My + MQy;# include <iostream> {.unnumbered .unlisted}
# include <cmath> {.unnumbered .unlisted}
using namespace std;
int main() {
double Ax, Ay, Bx, By;
double d;
double alpha;
cin >> Ax >> Ay >> Bx >> By;
cin >> d >> alpha;
// vektor BA
double BAx = Ax - Bx, BAy = Ay - By;
// duzina vektora BA
double BA = sqrt(BAx*BAx + BAy*BAy);
// ugao alpha/2 u radijanima
double alpha2 = (alpha/2) / 180 * M_PI;
// duzina vektora BM
double BM = d * cos(alpha2);
// duzina vektora MP i MQ
double MP = d * cos(alpha2), MQ = MP;
// vektor BM
double BMx = BM * BAx / BA, BMy = BM * BAy / BA;
// tacka M
double Mx = Bx + BMx, My = By + BMy;
// vektor MP
double MPx = MP * (-BAy / BA), MPy = MP * (BAx / BA);
// tacka P
double Px = Mx + MPx, Py = My + MPy;
// vektor MQ
double MQx = MQ * (BAy / BA), MQy = MQ * (-BAx / BA);
// tacka Q
double Qx = Mx + MQx, Qy = My + MQy;
cout << Px << " " << Py << endl;
cout << Qx << " " << Qy << endl;
return 0;
}Skalarni proizvod \(\overrightarrow{a} \circ \overrightarrow{b}\) vektora \(\overrightarrow{a}\) i \(\overrightarrow{b}\) je skalar (broj):
\[\overrightarrow{a}\circ \overrightarrow{b} = |\overrightarrow{a}|\cdot|\overrightarrow{b}|\cdot \cos\phi,\]
gde je sa \(|\overrightarrow{v}|\) označen intenzitet vektora \(\overrightarrow{v}\), a sa \(\phi\) konveksni ugao (manji ili jednak \(\pi\)) koji obrazuju vektori \(\overrightarrow{a}\) i \(\overrightarrow{b}\). Jednostavno se dokazuje da skalarni proizvod ima sledeće osobine:
\[\begin{eqnarray*} \overrightarrow{a} \circ \overrightarrow{b} = \overrightarrow{b} \circ \overrightarrow{a}&& \mathrm{simetričnost}\\ \overrightarrow{a}\circ (\overrightarrow{b}_1 + \overrightarrow{b}_2) = \overrightarrow{a}\circ\overrightarrow{b}_1 + \overrightarrow{a}\circ\overrightarrow{b}_1&&\mathrm{desna\ distributivnost}\\ (\overrightarrow{a}_1 + \overrightarrow{a}_2)\circ \overrightarrow{b} = \overrightarrow{a}_1\circ\overrightarrow{b} + \overrightarrow{a}_2\circ\overrightarrow{b}&&\mathrm{leva\ distributivnost}\\ \overrightarrow{a}\circ \overrightarrow{a} \geq 0 && \mathrm{nenegativnost}\\ \overrightarrow{a}\circ \overrightarrow{a} = 0 \Leftrightarrow \overrightarrow{a}=\overrightarrow{0} && \mathrm{pozitivna\ definitnost}\\ (k\cdot\overrightarrow{a})\circ \overrightarrow{b}=\overrightarrow{a}\circ(k\cdot \overrightarrow{b}) = k\cdot (\overrightarrow{a}\circ \overrightarrow{b})&&\mathrm{odnos\ sa\ skaliranjem} \end{eqnarray*}\]
Ako umemo da izračunamo skalarni proizvod proizvoljna dva vektora, jednostavno je izračunati:
intenzitet, tj. dužinu vektora \(\overrightarrow{u}\), na osnovu formule \(|\overrightarrow{u}|^2=\overrightarrow{u}\circ \overrightarrow{u}\), jer je \(\cos 0 = 1\),
konveksni ugao \(\phi\) između vektora \(\overrightarrow{u}\) i \(\overrightarrow{v}\), na osnovu formule \(\phi=\arccos\frac{\overrightarrow{u}\circ \overrightarrow{v}}{|\overrightarrow{u|}\cdot|\overrightarrow{v}|}\). Obratite pažnju na to da je vrednost funkcije \(\arccos\) uvek između \(0\) i \(\pi\), pa se skalarnim proizvodom uvek izračunava vrednost konveksnog ugla između vektora.
Specijalno, skalarni proizvod dva vektora različita od nule je nula ako i samo ako je \(\cos{\phi} = 0\), pa se skalarni proizvod može koristiti i za proveru da li su vektori međusobno normalni (pri čemu treba biti obazriv ako se radi sa brojevima zapisanim u pokretnom zarezu, jer se usled numeričkih grešaka može dobiti vrednost bliska, ali ne i jednaka nuli iako su vektori međusobno normalni). Negativna vrednost skalarnog proizvoda ukazuje na to da je manji (konveksni) ugao između vektora tup, a pozitivna da je taj ugao oštar.
Skalarni proizvod se lako izračunava analitički, kada su vektori zadati koordinatama u Dekartovom koordinatnom sistemu. Naime, ako su dva vektora \(\overrightarrow{a}(a_1,\ldots,a_n)\) i \(\overrightarrow{b}(b_1,\ldots,b_n)\) iste dimenzije, njihov skalarni proizvod je skalar čiju vrednost računamo po formuli:
\[\overrightarrow{a}\circ \overrightarrow{b}=\sum_{i=1}^{n}a_i\cdot b_i\]
Ovo se veoma jednostavno može dokazati izražavanjem vektora \(\overrightarrow{a}\) i \(\overrightarrow{b}\) preko svojih koordinata i korišćenjem osnovnih osobina skalarnog proizvoda.
Ukoliko su koordinate vektora \(\overrightarrow{a}\) i \(\overrightarrow{b}\) celobrojne, i vrednost skalarnog proizvoda je celobrojna.
U daljem tekstu ćemo razmatrati vektore određene tačkama u ravni, te će dimenzija vektora biti jednaka \(2\). Skalarni proizvod vektora \(\overrightarrow{a}(a_x, a_y)\) i vektora \(\overrightarrow{b}(b_x,b_y)\) dimenzije \(2\) jednak je \(\overrightarrow{a}\circ \overrightarrow{b}=a_x\cdot b_x+a_y\cdot b_y\).
Naredni aplet prikazuje jednu moguću vizuelizaciju skalarnog proizvoda. Skalarni proizvod dva vektora u ravni jednak je \(a_xb_x + a_yb_y\) i može se razdvojiti na dva sabirka. Prvi sabirak govori o odnosu komponenata vektora \(a\) i \(b\) duž \(x\)-ose, a drugi o odnosu komponenata duž \(y\)-ose. Komponente duž različitih osa su međusobno normalne i ne doprinose skalarnom proizvodu.
Proizvod brojeva \(a_xb_x\) se može grafički predstaviti pravougaonikom stranica \(|a_x|\) i \(|b_x|\) (da bi se on nacrtao vektor \(\overrightarrow{OB_x}\) je rotiran za \(90^\circ\) tj. \(\frac{\pi}{2}\) radijana). Znak proizvoda je pozitivan ako su koordinate \(a_x\) i \(b_x\) istog, a negativan ako su suprotnog znaka. Znak ćemo predstavljati bojom pravougaonika (zeleni pravougaonik ukazuje na pozitivnu, a žuti na negativnu vrednost sabirka). Analogno važi i za proizvod \(a_yb_y\).
Analitičko izračunavanje skalarnog proizvoda podrazumeva korišćenje koordinata vektora, koje su zapravo određene projekcijom vektora na koordinatne ose. Umesto toga, moguće je odrediti projekciju jednog vektora na pravac drugog. Time se dobijaju dva kolinearna vektora čiji se skalarni proizvod dobija množenjem njihovih intenziteta (vodeći računa o znaku).
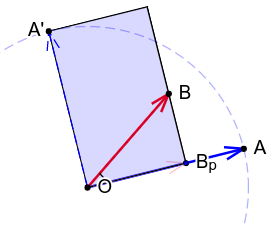
Na slici 3, tačka \(B_p\) je projekcija tačke \(B\) (krajnje tačke vektora \(\overrightarrow{OB}\)) na pravac vektora \(\overrightarrow{OA}\). Dužina \(OB_p\) je jednaka apsolutnoj vrednosti izraza \(|\overrightarrow{OB}|\cos{\phi}\) (gde je \(\phi\) konveksni ugao između vektora \(\overrightarrow{OA}\) i \(\overrightarrow{OB}\)), dok negativan znak tog izraza ukazuje na to da je vektor \(\overrightarrow{OB_p}\) suprotno usmeren od vektora \(\overrightarrow{OA}\), a pozitivan znak na to da su ta dva vektora isto usmerena. Zato je apsolutna vrednost skalarnog proizvoda \(\overrightarrow{OA} \circ \overrightarrow{OB} = |\overrightarrow{OA}| |\overrightarrow{OB}| \cos{\phi}\) jednaka proizvodu dužina \(OB_p\) i \(OA\), dok je znak skalarnog proizvoda negativan ako su vektori \(\overrightarrow{OB_p}\) i \(\overrightarrow{OA}\) suprotno usmereni, a pozitivan ako su isto usmereni. Projekcija pomaže i da se vrednost skalarnog proizvoda vizualizuje. Da bismo vizuelno predstavili apsolutnu vrednost skalarnog proizvoda, vektor \(\overrightarrow{OA}\) rotiramo za \(90^\circ\) tj. \(\frac{\pi}{2}\) radijana, čime se dobija vektor \(\overrightarrow{OA'}\), koji sa vektorom \(\overrightarrow{OB_p}\) gradi pravougaonik (prikazan plavom bojom na slici 3) čija je površina jednaka apsolutnoj vrednosti skalarnog proizvoda.
Naravno, pošto je sve simetrično, moguće je projektovati tačku \(A\) na pravac vektora \(\overrightarrow{OB}\).
Naredni aplet prikazuje drugačiju vizuelizaciju skalarnog proizvoda, koja razjašnjava vezu sa projekcijom vektora.
Videli smo da je skalarni proizvod u tesnoj vezi sa projekcijom tačke na pravu, tj. na pravac jednog od vektora koji se množe. Stoga se ta projekcija veoma jednostavno određuje korišćenjem skalarnog proizvoda.
Problem. Izračunati koordinate normalne projekcije \(M_p\) tačke \(M\) na pravu \(AB\) (slika 4).
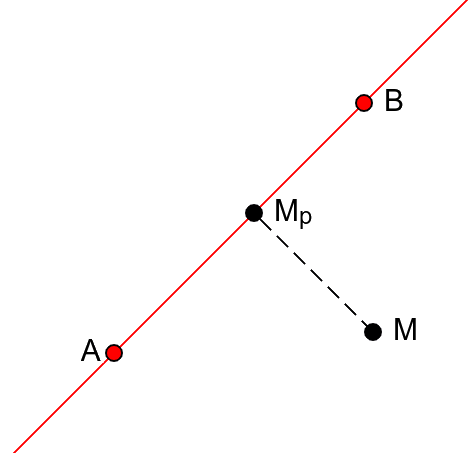
Za tačku \(M_p\) važi \(M_p = A + \overrightarrow{AM_p}\). Vektor \(\overrightarrow{AM_p}\) kolinearan je sa vektorom \(\overrightarrow{AB}\), a dužina vektora \(\overrightarrow{AM_p}\) jednaka je apsolutnoj vrednosti izraza \(|AM|\cos\phi\) (gde je \(\phi\) ugao između vektora \(\overrightarrow{AB}\) i \(\overrightarrow{AM}\)). Vrednost skalarnog proizvoda vektora \(\overrightarrow{AB}\) i \(\overrightarrow{AM}\) jednaka je \(|AB||AM|\cos\phi\), pa je dužina vektora \(\overrightarrow{AM_p}\) jednaka apsolutnoj vrednosti izraza
\[\frac{\overrightarrow{AB} \circ \overrightarrow{AM}}{|\overrightarrow{AB}|}\](1)
pri čemu znak ove vrednosti govori o tome da li su vektori \(\overrightarrow{AB}\) i \(\overrightarrow{AM_p}\) isto ili suprotno usmereni. Vektor \(\overrightarrow{AM_p}\) se može dobiti tako što se jedinični vektor \(\frac{\overrightarrow{AB}}{|\overrightarrow{AB}|}\) pomnoži vrednošću izraza (1). Zato je
\[M_p = A + \overrightarrow{AM_p} = A + \frac{\overrightarrow{AB} \circ \overrightarrow{AM}}{|\overrightarrow{AB}|^2}\overrightarrow{AB}.\]
Naglasimo da se ova formula može koristiti i za tačke u ravni i za tačke u prostoru.
Naredni aplet prikazuje projekciju tačke na pravu.
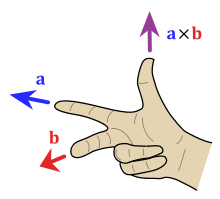
Vektorski proizvod vektora \(\overrightarrow{a}(a_x,a_y,a_z)\) i \(\overrightarrow{b}(b_x,b_y,b_z)\) dimenzije \(3\) je vektor upravan na ravan određenu vektorima \(\overrightarrow{a}\) i \(\overrightarrow{b}\), čiji je smer određen pravilom desne ruke (slika 5)1, a intenzitet jednak površini paralelograma koji određuju vektori \(\overrightarrow{a}\) i \(\overrightarrow{b}\), odnosno može se izračunati korišćenjem formule
\[|\overrightarrow{a}\times \overrightarrow{b}| = |\overrightarrow{a}|\cdot|\overrightarrow{b}|\cdot \sin\phi,\]
gde je sa \(\phi\) označen manji od uglova koji obrazuju vektori \(\overrightarrow{a}\) i \(\overrightarrow{b}\) (tj. konveksni ugao, čiji je sinus uvek pozitivan).
Lako se pokazuju osnovna svojstva vektorskog proizvoda:
\[\begin{eqnarray*} \overrightarrow{a}\times \overrightarrow{b} = -\overrightarrow{b}\times\overrightarrow{a}&&\mathrm{antikomutativnost}\\ \overrightarrow{a}\times (\overrightarrow{b}_1 + \overrightarrow{b}_2) = \overrightarrow{a}\times\overrightarrow{b}_1 + \overrightarrow{a}\times\overrightarrow{b}_1&&\mathrm{desna\ distributivnost}\\ (\overrightarrow{a}_1 + \overrightarrow{a}_2)\times \overrightarrow{b} = \overrightarrow{a}_1\times\overrightarrow{b} + \overrightarrow{a}_2\times\overrightarrow{b}&&\mathrm{leva\ distributivnost}\\ \overrightarrow{a}\times \overrightarrow{a} = 0&&\mathrm{samoproizvod}\\ (k\cdot\overrightarrow{a})\times \overrightarrow{b}=\overrightarrow{a}\times(k\cdot \overrightarrow{b}) = k\cdot (\overrightarrow{a}\times \overrightarrow{b})&&\mathrm{odnos\ sa\ skaliranjem} \end{eqnarray*}\]
Naglasimo i da nam skalarni proizvod daje način da lako odredimo kosinus ugla između dva vektora, a odatle i veličinu konveksnog ugla između njih. Sa druge strane, iz vektorskog proizvoda se lako određuje vrednost sinusa ugla između dva vektora, međutim, vrednost sinusa nije dovoljna da se lako odredi konveksni ugao (jer istu vrednost sinusa daju jedan oštar i jedan tup ugao). Stoga se za određivanje veličine konveksnog ugla između dva vektora koristi skalarni, a ne vektorski proizvod.
Pošto važi da je:
\[\begin{eqnarray*} \overrightarrow{a}&=&a_x\cdot \overrightarrow{i}+a_y\cdot \overrightarrow{j}+a_z\cdot \overrightarrow{k} \\ \overrightarrow{b}&=&b_x\cdot \overrightarrow{i}+b_y\cdot \overrightarrow{j}+b_z\cdot \overrightarrow{k} \end{eqnarray*}\]
gde su sa \(\overrightarrow{i}\), \(\overrightarrow{j}\) i \(\overrightarrow{k}\) označeni međusobno normalni jedinični vektori u smeru \(x\), \(y\) i \(z\) koordinatne ose, i istovremeno je:
\[\begin{eqnarray*} \overrightarrow{i}\times \overrightarrow{j}=\overrightarrow{k}=-\overrightarrow{j}\times \overrightarrow{i} \\ \overrightarrow{j}\times \overrightarrow{k}=\overrightarrow{i}=-\overrightarrow{k}\times \overrightarrow{j} \\ \overrightarrow{k}\times \overrightarrow{i}=\overrightarrow{j}=-\overrightarrow{i}\times \overrightarrow{k} \end{eqnarray*}\]
važi da je vektorski proizvod vektora \(\overrightarrow{a}\) i \(\overrightarrow{b}\) jednak:
\[\overrightarrow{a}\times \overrightarrow{b} = (a_yb_z-a_zb_y)\overrightarrow{i}+(a_zb_x-a_xb_z)\overrightarrow{j}+(a_xb_y-a_yb_x)\overrightarrow{k}\]
Ova formula se može zapisati u obliku naredne determinante:
\[\overrightarrow{a}\times \overrightarrow{b} = \begin{vmatrix} \overrightarrow{i} & \overrightarrow{j} & \overrightarrow{k} \\ a_x & a_y & a_z \\ b_x & b_y & b_z \end{vmatrix}\]
u čijoj se prvoj vrsti nalaze jedinični vektori u smeru \(x\), \(y\) i \(z\) ose, u drugoj vrsti koordinate vektora \(\overrightarrow{a}\), a u trećoj koordinate vektora \(\overrightarrow{b}\). Ukoliko su koordinate vektora \(\overrightarrow{a}\) i \(\overrightarrow{b}\) celobrojne, i koordinate vektora \(\overrightarrow{a}\times \overrightarrow{b}\) su celobrojne.
Vektorski proizvod je definisan za vektore u trodimenzionom prostoru. Ipak, i vektori u ravni se mogu vektorski množiti ako se ravan \(xOy\) utopi u trodimenzioni prostor. Time se koordinate svakog od dva vektora ravni prošire nulom (\(z\) koordinata tih vektora je nula) i izvrši se vektorsko množenje. Rezultat je vektor koji je upravan na ravan \(xOy\), tj. vektor čije su prve dve koordinate jednake nuli. Zaista
\[\overrightarrow{a}\times \overrightarrow{b} = \begin{vmatrix} \overrightarrow{i} & \overrightarrow{j} & \overrightarrow{k} \\ a_x & a_y & 0 \\ b_x & b_y & 0 \end{vmatrix} = (0, 0, a_xb_y-a_yb_x).\]
Pošto nam je u ovom slučaju jedino značajna \(z\)-koordinata, vektorski proizvod dva ravanska vektora \(\overrightarrow{a} = (a_x, a_y)\) i \(\overrightarrow{b} = (b_x, b_y)\) se ponekad poistovećuje sa skalarom \(a_xb_y - a_yb_x\) (što može biti zbunjuće, jer nazivi skalarni i vektorski proizvod potiču od toga što je u prvom slučaju rezultat množenja skalar, a u drugom vektor). Da bismo izbegli zabunu, naglašavaćemo uvek da je u pitanju množenje dvodimenzionalnih vektora (tj. dvodimenzionalni vektorski proizvod2) i umesto oznake \(\times\) koristićemo \(\times_{2d}\). Dakle, za dvodimenzionalne vektore \(\overrightarrow{a} = (a_x, a_y)\) i \(\overrightarrow{b}=(b_x, b_y)\) definišemo da je:
\[\overrightarrow{a} \times_{2d} \overrightarrow{b} = a_xb_y - a_yb_x = \begin{vmatrix} a_x & a_y\\ b_x & b_y \end{vmatrix}.\]
Ako dvodimenzionalni vektori obrazuju ugao \(\phi\), vrednost dvodimenzionalnog vektorskog proizvoda \(\overrightarrow{a}\times_{2d}\overrightarrow{b}\) jednaka je \(|\overrightarrow{a}|\cdot |\overrightarrow{b}|\cdot \sin{\phi}\).
Vrednost \(\overrightarrow{a}\times_{2d}\overrightarrow{b}=0\) nam govori da su vektori \(\overrightarrow{a}\) i \(\overrightarrow{b}\) kolinearni, tj. da je ugao koji obrazuju \(0\) ili \(\pi\) i to se obično koristi kao potreban i dovoljan uslov za ispitivanje kolinearnosti vektora. Zaista, pošto je \(\overrightarrow{a} \times_{2d} \overrightarrow{b} = |\overrightarrow{a}|\cdot|\overrightarrow{b}|\cdot \sin \phi\), važi da je:
\[\sin \phi = \frac{\overrightarrow{a} \times_{2d} \overrightarrow{b}}{|\overrightarrow{a}|\cdot|\overrightarrow{b}|}.\]
Sinus je jednak nuli za ugao \(0\) ili \(\pi\).
Zato jedna od osnovnih primena vektorskog proizvoda može biti da se utvrdi da li su tri tačke kolinearne.
Problem. Date su tri tačke u prostoru (ili u ravni). Ispitati da li su one kolinearne.
Tačka \(M\) u trodimenzionalnom prostoru pripada pravoj koja je određena tačkama \(A\) i \(B\) ako i samo ako je \(\overrightarrow{MA} \times \overrightarrow{MB} = \overrightarrow{0}\) (ili, na primer, \(\overrightarrow{AB} \times \overrightarrow{AM} = \overrightarrow{0}\)). Za tačke \(A\), \(B\) i \(M\) u ravni, dovoljno je proveriti uslov \(\overrightarrow{MA}\times_{2d}\overrightarrow{MB} = 0\). Pri tome treba biti obazriv ako se radi sa realnim koordinatama (jer je zbog računskih grešaka malo verovatno da će se dobiti vrednosti koje su baš tačno jednake nuli).
Provera kolinearnosti se veoma lako dopunjuje do provere da li tačka pripada duži.
Problem. Date su različite tačke \(A\), \(B\) i tačka \(M\) u ravni. Ispitati da li tačka \(M\) pripada zatvorenoj duži \(AB\).
Tačka \(M\) pripada duži \(AB\) ako i samo ako je kolinearna sa \(A\) i \(B\), ako se njena projekcija na \(x\)-osu nalazi između projekcija tačaka \(A\) i \(B\) na \(x\)-osu i ako se njena projekcija na \(y\)-osu nalazi između projekcija tačaka \(A\) i \(B\) na \(y\)-osu (tj. ako tačka \(M\) pripada pravougaoniku čija je dijagonala \(AB\)). Ako znamo da duž \(AB\) nije vertikalna, tada je dovoljno proveriti samo projekcije na \(x\)-osu.
bool kolinearne(const Tacka& A, const Tacka& B, const Tacka& M) {
return (B.x-A.x)*(M.y-A.y) == (M.x-A.x)*(B.y-A.y);
}
bool pripadaDuzi(const Tacka& A, const Tacka& B, const Tacka& M) {
return kolinearne(A, B, M) &&
min(A.x, B.x) <= M.x && M.x <= max(A.x, B.x) &&
min(A.y, B.y) <= M.y && M.y <= max(A.y, B.y);
}U prethodnoj implementaciji se smatra da je duž \(AB\) zatvorena. Ako se razmatra otvorena duž \(AB\), tada nejednakosti u proveri projekcija treba da budu stroge.
Znak vrednosti dvodimenzionalnog vektorskog proizvoda \(\overrightarrow{a}\times_{2d}\overrightarrow{b}\) nam govori o orijentisanom uglu između vektora \(\overrightarrow{a}\) i \(\overrightarrow{b}\), pri čemu se sada ugao posmatra u intervalu \([0, 2\pi)\) (slika 6). Pozitivne vrednosti govore da je ugao koji se opisuje rotiranjem vektora \(\overrightarrow{a}\) ka vektoru \(\overrightarrow{b}\) u pozitivnom matematičkom smeru konveksan (u intervalu je \((0, \pi)\)), a negativne vrednosti da je taj ugao nekonveksan (u intervalu je \((\pi, 2\pi)\)). Ovo, naravno, odgovara znaku sinusa ugla.
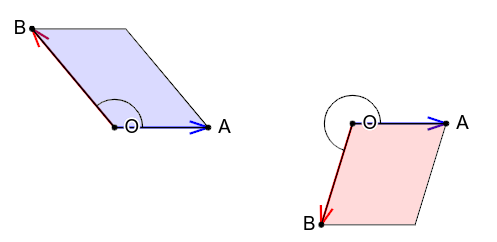
Još jedna interpretacija je da pozitivni znak dvodimenzionalnog vektorskog proizvoda \(\overrightarrow{a}\times_{2d}\overrightarrow{b}\) ukazuje da je najbliži put od vektora \(\overrightarrow{a}\) do vektora \(\overrightarrow{b}\) “nalevo” tj. u pozitivnom matematičkom smeru, dok negativni znak dvodimenzionalnog vektorskog prostora ukazuje na to da je najbliži put “nadesno”.
Naredni aplet vizualizuje dvodimenzionalni vektorski proizvod. Plavom bojom paralelograma je predstavljena pozitivna vrednost dvodimenzionalnog vektorskog proizvoda (i konveksan ugao), a crvenom negativna (i nekonveksan ugao).
Znak dvodimenzionalnog vektorskog proizvoda se može iskoristiti i da se tačke klasifikuju u dve poluravni na koje prava \(AB\) deli ravan. Negativna vrednost vektorskog proizvoda \(\overrightarrow{OA}\times_{2d}\overrightarrow{OB}\) ukazuje da tačka \(O\) pripada jednoj poluravni, a pozitivna da pripada drugoj (dok vrednost \(0\) ukazuje na to da tačka \(O\) pripada graničnoj pravoj \(AB\)).
Da rezimiramo, sledeći uslovi su međusobno ekvivalentni:
U poglavlju 30 videćemo da se znak vektorskog proizvoda koristi i za određivanje orijentacije trojke tačaka, što je fundamentalna operacija u mnogim geometrijskim algoritmima.
Problem. Izračunati površinu trougla čija su temena tri tačke u ravni zadate svojim koordinatama.
Površina trougla čije su stranice dva data vektora \(\overrightarrow{a}\) i \(\overrightarrow{b}\) je polovina površine paralelograma koji oni grade i jednaka je polovini apsolutne vrednosti njihovog vektorskog proizvoda. Ako su poznate koordinate temena trougla \(A(a_x, a_y)\), \(B(b_x, b_y)\) i \(C(c_x, c_y)\), vektori stranica su \(\overrightarrow{AB} = \overrightarrow{OB} - \overrightarrow{OA} = (b_x - a_x, b_y - a_y)\) i \(\overrightarrow{AC} = \overrightarrow{OC} - \overrightarrow{OA} = (c_x - a_x, c_y - a_y)\), pa je površina jednaka
\[P_{ABC} = \frac{|\overrightarrow{AB} \times_{2d} \overrightarrow{AC}|}{2} = \frac{|(b_x - a_x)(c_y - a_y) - (b_y - a_y)(c_x - a_x)|}{2}.\]
double PovrsinaTrougla(const Tacka& A, const Tacka& B, const Tacka& C) {
return abs((B.x - A.X)*(C.y - A.y) - (B.y - A.y)*(C.x - A.x) / 2.0;
}Površina ne mora biti ceo broj čak ni kada su koordinate celobrojne (zbog deljenja sa 2). Da bi se izbegao rad sa realnim brojevima, nekada se u kodu definiše funkcija koja izračunava dvostruku površinu a kasnije formule se, ako je moguće, modifikuju tako da umesto površine koriste dvostruku površinu.
Izrazom \(\frac{|\overrightarrow{AB} \times \overrightarrow{AC}|}{2}\) se može računati i površina trougla u prostoru (ali je tada izraz kojim se površina izražava pomoću koordinata tačaka komplikovaniji).
Površinu je moguće izračunati i na druge načine, ali je to često ili neefikasno ili se konačna formula svodi na prethodnu. Na primer, Heronov obrazac \(s = (a+b+c)/2\), \(P=\sqrt{s(s-a)(s-b)(s-c)}\) uključuje korenovanje, što ovaj prisup čini neefikasnim.
Još jedan način dolaska do rešenja je da se površina trougla iskaže kao razlika površina određenih trapeza. Na primer, ako važi raspored \(a_x < b_x < c_x\), i ako su \(A_x\), \(B_x\) i \(C_x\) redom projekcije tačaka \(A\), \(B\) i \(C\) na \(x\)-osu, tada je površina trougla \(ABC\) jednaka razlici između zbira površina pravouglih trapeza \(AA_xB_xB\), \(BB_xC_xC\) i površine pravouglog trapeza \(AA_xC_xC\) (slika 7).
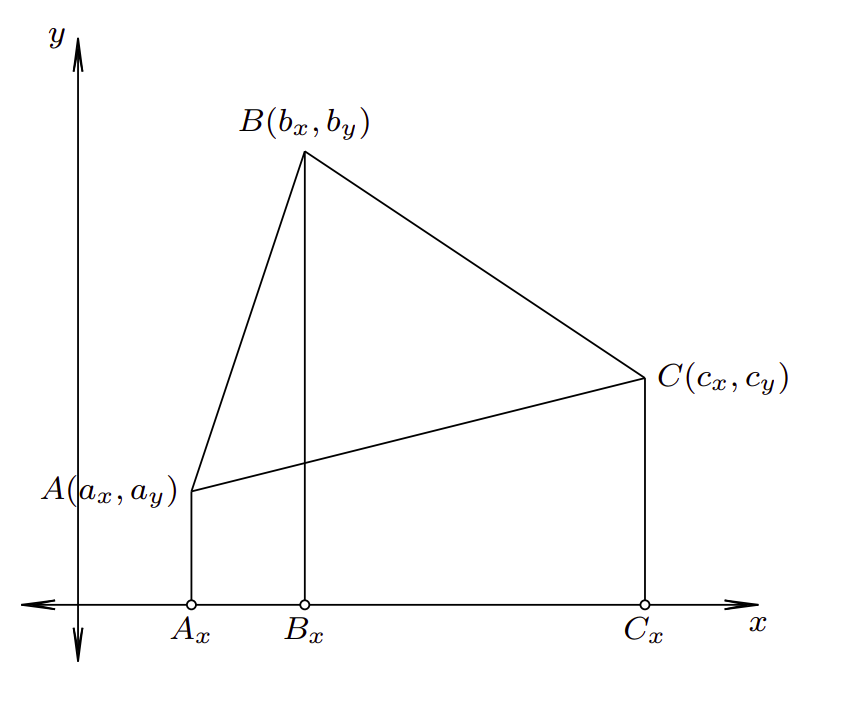
Površina trapeza \(AA_xB_xB\) jednaka je proizvodu dužine njegove srednje linije i dužine njegove visine. Dužina osnovice \(A_xA\) jednaka je apsolutnoj vrednosti koordinate \(a_y\), dužina osnovice \(B_xB\) jednaka je apsolutnoj vrednosti koordinate \(b_y\) dok je dužina visine jednaka apsolutnoj vrednosti razlike koordinata \(b_x\) i \(a_x\). Tako da je površina tog trapeza jednaka
\[\frac{|b_x - a_x|(|a_y| + |b_y|)}{2}\](2)
Na sličan način mogu se izvesti i formule za druga dva trapeza.
Analizom mogućih rasporeda tačaka, može se pokazati da će se ispravan rezultat dobiti i ako se posmatra takozvana označena površina trapeza, koja isključuje računanje apsolutne vrednosti u formuli (2) i dopušta negativne dužine i površine. Naime, označena površina trougla \(ABC\) biće jednaka zbiru označenih površina tri pomenuta pravougla trapeza (\(AA_xB_xB\), \(BB_xC_xC\) i \(CC_xA_xA\)), a prava površina trougla biće jednaka njenoj apsolutnoj vrednosti. Označene površine ovih trapeza dobijaju se tako što se u prethodno izvedenim formulama za njihovu površinu zanemare apsolutne vrednosti, tako da se površina trougla dobija sledećom formulom.
\[P_{ABC} = \frac{|(b_x - a_x)(b_y + a_y) + (c_x - b_x)(c_y + b_y) + (a_x - c_x)(a_y + c_y)|}{2}\]
Nakon sređivanja dobija se formula
\[ P_{ABC} = \frac{|a_xb_y + b_xc_y + c_xa_y - a_xc_y - c_xb_y - b_xa_y|}{2} \]
Ova formula se nekada naziva pravilo pertle (engl. shoelace formula). Zaista, ako se koordinate tačaka zapišu u narednom obliku

formula se gradi tako što se sa jednim znakom uzimaju proizvodi odozgo-naniže, sleva-udesno (to su \(a_xb_y\), \(b_xc_y\) i \(c_xa_y\)), dok se sa suprotnim znakom uzimaju proizvodi odozdo-naviše, sleva udesno (to su \(a_xc_y\), \(c_xb_y\) i \(b_xa_y\)), što, kada se nacrta, zaista podseća na cik-cak vezivanje pertli.
Primetimo da se nakon sređivanja formule dobijene kada se površina trougla računa pomoću vektorskog proizvoda takođe dobija formula pertle. Videćemo da se formula pertle može uopštiti i na izračunavanje površine određenih vrsta mnogouglova.
Problem. Za date tačke \(A\), \(B\) i \(C\) u ravni, odrediti najkraće rastojanje od \(C\) do prave \(AB\).
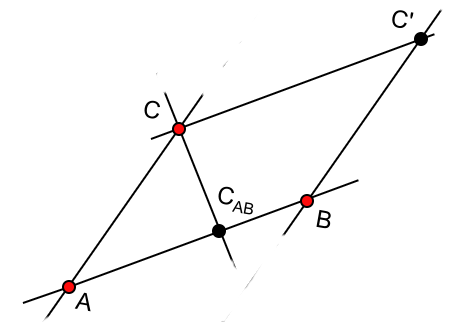
Površina paralelograma određenog vektorima \(\overrightarrow{AB}\) i \(\overrightarrow{AC}\) (slika 8) je sa jedne strane jednaka apsolutnoj vrednosti dvodimenzionalnog vektorskog proizvoda vektora njegovih stranica, dok je sa druge strane jednaka proizvodu dužine njegove osnove \(AB\) i visine \(CC_{AB}\). Ovo se može upotrebiti da bi se izračunalo rastojanje tačke \(C\) od prave određene tačkama \(A\) i \(B\), jer to rastojanje predstavlja visinu \(CC_{AB}\) paralelograma određenog vektorima \(\overrightarrow{AB}\) i \(\overrightarrow{AC}\). Pošto je dužina osnovice jednaka \(|\overrightarrow{AB}|\), visina tj. rastojanje tačke \(C\) do prave \(AB\) je jednako
\[\frac{|\overrightarrow{AB}\times_{2d}\overrightarrow{AC}|}{|\overrightarrow{AB}|} = \frac{|(b_x - a_x)(c_y - a_y) - (b_y - a_y)(c_x - a_x)|}{\sqrt{(b_x - a_x)^2+(b_y - a_y)^2}}\]
Narednom funkcijom se određuje rastojanje date tačke od date prave.
// rastojanje tacke C od prave odredjene tackama A i B
double rastojanje(const Tacka& A, const Tacka& B, const Tacka& C) {
double dx = B.x - A.x;
double dy = B.y - A.y;
return abs(dx*(C.y-A.y) - dy*(C.x-A.x)) / sqrt(dx*dx + dy*dy);
}# include <iostream> {.unnumbered .unlisted}
# include <iomanip> {.unnumbered .unlisted}
# include <cmath> {.unnumbered .unlisted}
# include <algorithm> {.unnumbered .unlisted}
using namespace std;
struct Tacka {
double x, y;
};
// rastojanje tacke C od prave odredjene tackama A i B
double rastojanje(const Tacka& A, const Tacka& B, const Tacka& C) {
double dx = B.x - A.x;
double dy = B.y - A.y;
return abs(dx*(C.y-A.y) - dy*(C.x-A.x)) / sqrt(dx*dx + dy*dy);
}
int main() {
Tacka A, B, C;
cin >> A.x >> A.y;
cin >> B.x >> B.y;
int n;
cin >> n;
cin >> C.x >> C.y;
double r = rastojanje(A, B, C);
double najmanje = r, najvece = r;
for (int i = 1; i < n; i++) {
cin >> C.x >> C.y;
r = rastojanje(A, B, C);
najmanje = min(najmanje, r);
najvece = max(najvece, r);
}
cout << fixed << showpoint << setprecision(5)
<< najmanje << endl
<< najvece << endl;
return 0;
}Izrazom \(\frac{|\overrightarrow{AB}\times\overrightarrow{AC}|}{|\overrightarrow{AB}|}\) se može računati i rastojanje od tačke do prave u prostoru.
Problem. Za dati skup tačaka \(S\) u ravni, odrediti najkraće rastojanje od neke tačke \(C\in S\) do prave \(AB\).
Ako je potrebno odrediti najbližu ili najdalju tačku nekog skupa od prave \(AB\) (a ne i njihova rastojanja), dovoljno je izračunati i porediti samo vrednosti brojioca, jer će za sve tačke vrednost imenioca biti ista.
U narednom apletu se određuju najbliža i najdalja tačka u odnosu na pravu \(AB\). Najbliža tačka je obojena u plavo, a najdalja u žuto.
Uređena trojka nekolinearnih tačaka u ravni može imati:
orijentaciju u smeru suprotnom od kretanja kazaljke na časovniku – matematički pozitivna orijentacija (slika 9 (a))
orijentaciju u smeru kretanja kazaljke na časovniku – matematički negativna ordijentacija (slika 9 (b))
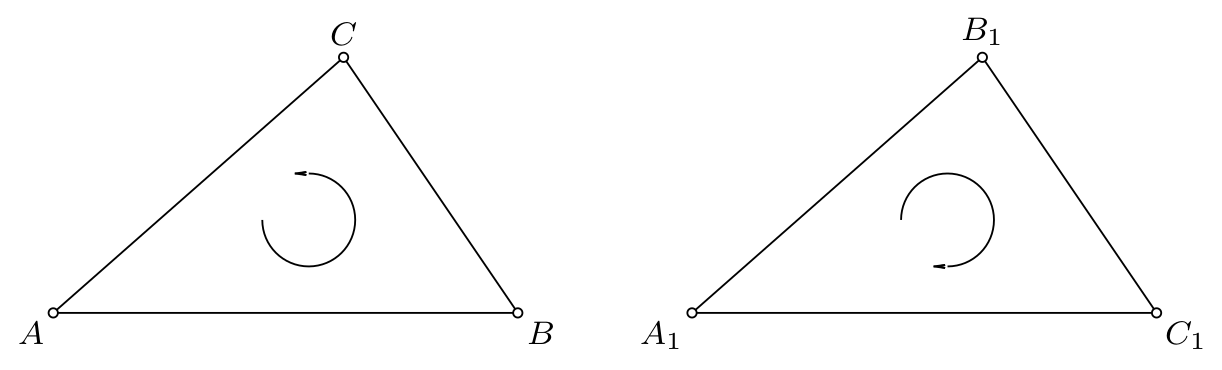
Važe naredna svojstva:
ako uređena trojka \(ABC\) ima pozitivnu (negativnu) orijentaciju, onda i uređena trojka \(BCA\) ima pozitivnu (negativnu) orijentaciju (pa i trojka \(CAB\));
ako uređena trojka \(ABC\) ima pozitivnu (negativnu) orijentaciju, onda uređena trojka \(BAC\) ima negativnu (pozitivnu) orijentaciju (pa i trojke \(ACB\) i \(CBA\)).
Orijentacija se može zasnovati i aksiomatski3, ali se lako može analitički izračunati kada su poznate koordinate tačaka \(A(a_x, a_y)\), \(B(b_x, b_y)\), \(C(c_x, c_y)\). Orijentaciju trojke \(ABC\) definišemo kao znak dvodimenzionalnog vektorskog proizvoda:
\[\overrightarrow{AB}\times_{2d} \overrightarrow{AC} = (b_x-a_x)(c_y-a_y) - (b_y-a_y)(c_x-a_x).\]
Pošto postoje tri moguće orijentacije, u cilju postizanja čitljivog programa moguće je definisati nabrojivi tip za predstavljanje orijentacije.
// moguce orijentacije trojke tacaka
enum Orijentacija {POZITIVNA, KOLINEARNE, NEGATIVNA};U nekim slučajevima možemo smatrati i da je orijentacija ceo broj i to \(1\) za pozitivnu orijentaciju, \(-1\) za negativnu i \(0\) za kolinearne tačke.
Kada su koordinate tačaka celobrojne, funkcija za izračunavanje orijentacije se veoma jednostavno definiše.
// orijentacija trojke tačka sa koordinatama A, B i C
// orijentacija je pozitivna akko je orijentisani ugao ABC konveksan
Orijentacija orijentacija(const Tacka& A, const Tacka& B, const Tacka& C) {
int d = (B.x-A.x)*(C.y-A.y) - (C.x-A.x)*(B.y-A.y);
if (d > 0)
return POZITIVNA;
else if (d < 0)
return NEGATIVNA;
else
return KOLINEARNE;
}# include <iostream> {.unnumbered .unlisted}
using namespace std;
struct Tacka {
int x, y;
};
// moguce orijentacije trojke tacaka
enum Orijentacija {POZITIVNA, KOLINEARNE, NEGATIVNA};
// orijentacija trojke tačka sa koordinatama A, B i C
// orijentacija je pozitivna akko je orijentisani ugao ABC konveksan
Orijentacija orijentacija(const Tacka& A, const Tacka& B, const Tacka& C) {
int d = (B.x-A.x)*(C.y-A.y) - (C.x-A.x)*(B.y-A.y);
if (d > 0)
return POZITIVNA;
else if (d < 0)
return NEGATIVNA;
else
return KOLINEARNE;
}
// provera da li su tačke M i N sa iste strane prave
// određene tačkama A i B.
// Pretpostavlja se da nijedna od dve tačke ne pripada toj pravoj.
bool saIsteStrane(const Tacka& A, const Tacka& B,
const Tacka& M, const Tacka& N) {
return orijentacija(A, B, M) == orijentacija(A, B, N);
}
int main() {
Tacka A, B;
cin >> A.x >> A.y;
cin >> B.x >> B.y;
Tacka M;
cin >> M.x >> M.y;
int n;
cin >> n;
int broj = 0;
for (int i = 0; i < n; i++) {
Tacka N;
cin >> N.x >> N.y;
if (saIsteStrane(A, B, M, N))
broj++;
}
cout << broj << endl;
return 0;
}Stvar je komplikovanija kada se radi sa koordinatama koje su zapisane pomoću brojeva u pokretnom zarezu. Naime, klasifikovanje orijentacije, a posebno ispitivanje kolinearnosti može biti veoma problematično usled grešaka u zapisu brojeva. Naime, umesto da vrednost dvodimenzionalnog vektorskog proizvoda bude tačno nula, ona može da bude neki veoma mali broj blizak nuli. Najjednostavnije je da se tada fiksira neka vrednost \(\varepsilon\) i da se, kada god je vrednost proizvoda u intervalu \([-\varepsilon, \varepsilon]\), tačke proglase za kolinearne. Međutim, nije unapred jasno kolika bi trebalo da bude ta vrednost \(\varepsilon\). Vrednost vektorskog proizvoda ne zavisi samo od ugla između vektora, već i od njihove dužine, pa bi precizniji pristup bi bio da se na osnovu vrednosti dvodimenzionalnog vektorskog proizvoda izračuna sinus ugla između vektora i da se za proveru kolinearnosti zahteva da on pripada nekom malom intervalu, međutim, to je računski zahtevnije. Primetimo da u nekim primenama nije previše bitno kako će se klasifikovati tačke koje su skoro kolinearne. Na primer, u računarskoj grafici, kako god da se klasifikuju tačke koje su gotovo kolinearne, ljudsko oko neće primetiti razliku.
Problem. Za date tačke \(M\) i \(N\) utvrditi da li su sa iste strane prave \(p\) određene tačkama \(A\) i \(B\) (\(A \neq B\)).
Jednostavnosti radi pretpostavićemo da nijedna od tačaka \(M\) i \(N\) ne pripada na pravoj \(AB\).
Tačke \(M\) i \(N\) su sa iste strane prave \(p\) ako i samo ako su trouglovi \(ABM\) i \(ABN\), \(A,B\in p\) iste orijentacije (slika 10). Dakle, dovoljno je da ispitamo da li su odgovarajući dvodimenzionalni vektorski proizvodi istog znaka.
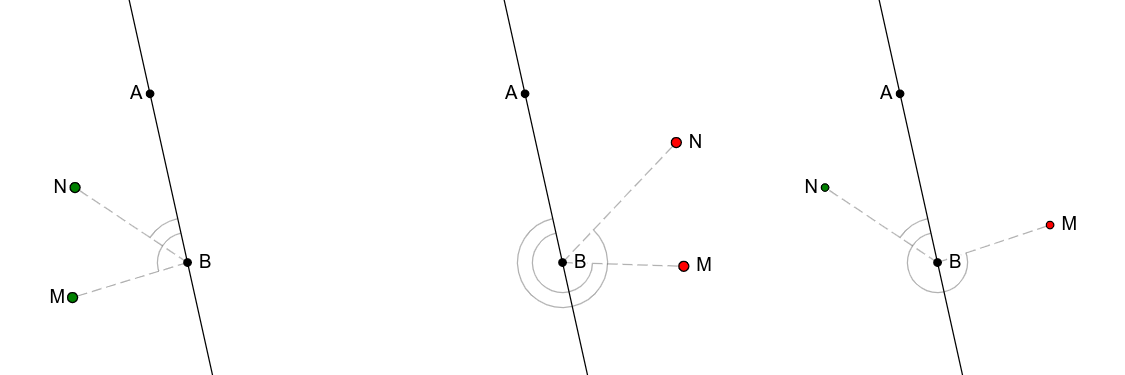
U narednom apletu implementirana je provera da li su tačke \(M\) i \(N\) sa iste ili sa različite strane prave \(AB\). Boja tačke \(M\) tj. \(N\) određena je orijentacijom trojke \(ABM\) tj. \(ABN\). Kada su tačke \(M\) i \(N\) sa iste strane, prikazuju se malo veće nego kada su sa različitih strana prave \(AB\).
Kada imamo na raspolaganju funkciju za računanje orijentacije, implementacija provere da li su dve tačke sa iste strane prave je veoma jednostavna.
// provera da li su tačke M i N sa iste strane prave
// određene tačkama A i B.
// Pretpostavlja se da nijedna od dve tačke ne pripada toj pravoj.
bool saIsteStrane(const Tacka& A, const Tacka& B,
const Tacka& M, const Tacka& N) {
return orijentacija(A, B, M) == orijentacija(A, B, N);
}# include <iostream> {.unnumbered .unlisted}
using namespace std;
struct Tacka {
int x, y;
};
// moguce orijentacije trojke tacaka
enum Orijentacija {POZITIVNA, KOLINEARNE, NEGATIVNA};
// orijentacija trojke tačka sa koordinatama A, B i C
// orijentacija je pozitivna akko je orijentisani ugao ABC konveksan
Orijentacija orijentacija(const Tacka& A, const Tacka& B, const Tacka& C) {
int d = (B.x-A.x)*(C.y-A.y) - (C.x-A.x)*(B.y-A.y);
if (d > 0)
return POZITIVNA;
else if (d < 0)
return NEGATIVNA;
else
return KOLINEARNE;
}
// provera da li su tačke M i N sa iste strane prave
// određene tačkama A i B.
// Pretpostavlja se da nijedna od dve tačke ne pripada toj pravoj.
bool saIsteStrane(const Tacka& A, const Tacka& B,
const Tacka& M, const Tacka& N) {
return orijentacija(A, B, M) == orijentacija(A, B, N);
}
int main() {
Tacka A, B;
cin >> A.x >> A.y;
cin >> B.x >> B.y;
Tacka M;
cin >> M.x >> M.y;
int n;
cin >> n;
int broj = 0;
for (int i = 0; i < n; i++) {
Tacka N;
cin >> N.x >> N.y;
if (saIsteStrane(A, B, M, N))
broj++;
}
cout << broj << endl;
return 0;
}Proširimo sada zahtev time da želimo da ako su tačke sa raznih strana prave odredimo i presečnu tačku duži koja ih spaja i prave (pri čemu je potrebno razmotriti i mogućnost da \(M\) ili \(N\) pripada pravoj \(AB\)).
Problem. Za date tačke \(M\) i \(N\) utvrditi da li su sa različitih strana prave \(p\) određene tačkama \(A\) i \(B\) (\(A \neq B\)) i ako jesu, odrediti koordinate presečne tačke duži \(MN\) i prave \(p\).
Naredni metod je zasnovan na korišćenju dvodimenzionalnog vektorskog proizvoda, ali ne za izračunavanje orijentacije trojke tačaka, jer ćemo koristiti proizvode vektora oblika \(\overrightarrow{XY} \times_{2d} \overrightarrow{ZW}\) (koji, podsetimo se, daju vrednost označene površine paralelograma određenog pomoću ta dva vektora).
Degenerisani slučaj nastupa kada su vektori \(\overrightarrow{AB}\) i \(\overrightarrow{MN}\) kolinearni, što se dešava ako i samo ako je \(\overrightarrow{AB} \times_{2d} \overrightarrow{MN} = 0\). Ako su u tom slučaju tačke \(M\), \(A\) i \(B\) kolinearne tj. ako je \(\overrightarrow{MA} \times_{2d} \overrightarrow{MB} = 0\), tada duž pripada pravoj, a ako nisu kolinearne, onda presek ne postoji.
U nedegenerisanom slučaju je \(\overrightarrow{AB} \times_{2d} \overrightarrow{MN} \neq 0\). Tada postoji presečna tačka \(X\) pravih \(AB\) i \(MN\) i važi da je:
\[X = M + k\overrightarrow{MN},\quad\mathrm{tj.}\quad \overrightarrow{MX}=k\overrightarrow{MN}.\]
Tačka \(X\) pripada duži \(MN\) ako i samo ako je \(0 \leq k \leq 1\). Pošto je \(\overrightarrow{MX} = \overrightarrow{MA} + \overrightarrow{AX}\), množenjem prethodne jednačine vektorski sa \(\overrightarrow{AB}\) sleva, dobija se:
\[\overrightarrow{AB}\times_{2d} (\overrightarrow{MA} + \overrightarrow{AX}) = k \cdot (\overrightarrow{AB}\times_{2d}\overrightarrow{MN})\]
Pošto važi da je \(\overrightarrow{AB}\times_{2d}\overrightarrow{AX} = 0\), jer tačka \(X\) pripada pravoj \(AB\), pa su ti vektori kolinearni, možemo izračunati koeficijent \(k\).
\[k = \frac{\overrightarrow{AB}\times_{2d}\overrightarrow{MA}}{\overrightarrow{AB}\times_{2d}\overrightarrow{MN}}\]
Da bi se proverilo da li tačka \(X\) pripada duži \(MN\) dovoljno je proveriti:
Ova tehnika ima i jasnu geometrijsku interpretaciju (slika 11).
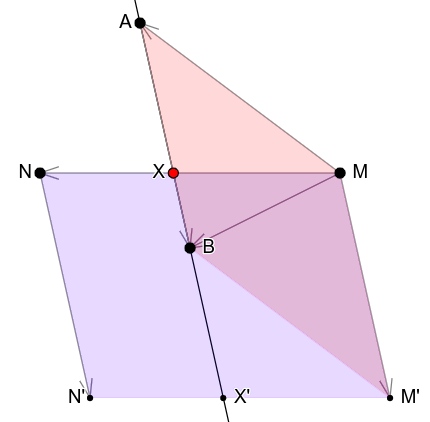
Neka je \(M' = M + \overrightarrow{AB}\) i \(N' = N + \overrightarrow{AB}\). Vrednost \(\overrightarrow{AB}\times_{2d}\overrightarrow{MA}\) predstavlja označenu površinu paralelograma određenog vektorima \(\overrightarrow{AB}\) i \(\overrightarrow{MA}\) (on je obojen na slici 11). Ta je površina jednaka označenoj površini paralelograma \(P_1\) određenog vektorima \(\overrightarrow{MX}\) i \(\overrightarrow{XX'}\). Vrednost \(\overrightarrow{AB}\times_{2d}\overrightarrow{MN}\) predstavlja označenu površinu paralelograma \(P_2\) određenog vektorima \(\overrightarrow{AB} = \overrightarrow{MM'}\) i \(\overrightarrow{MN}\) (i on je obojen na slici 11). Pošto paralelogrami \(P_1\) i \(P_2\) imaju istu visinu, odnos njihovih površina jednak je odnosu dužina njihovih stranica \(MX\) i \(MN\).
U narednom apletu data je geometrijska interpretacija provere da li su tačke \(M\) i \(N\) sa iste ili sa različite strane prave \(AB\), uz određivanje presečne tačke \(X\).
Naravno, da bi se duži sekle, potrebno je i da koeficijent
\[k = \frac{\overrightarrow{AM}\times_{2d}\overrightarrow{MN}}{\overrightarrow{AB}\times_{2d}\overrightarrow{MN}}\]
pripada intervalu \([0, 1]\), što posebno treba proveriti.
Problem. Dat je trougao \(ABC\) i tačka \(P\). Ispitati da li tačka \(P\) pripada unutrašnjosti trougla \(ABC\) ili ne.
Kao što je to obično slučaj u geometriji, treba obratiti pažnju na degenerisane i granične slučajeve. Na primer, mi ćemo, jednostavnosti radi, pretpostavljati da je trougao nedegenerisan, tj. da su tačke \(A\), \(B\) i \(C\) nekolinearne. Smatraćemo da troguao čine temena i tačke na stranicama. Pored njih, razlikovaćemo tačke u unutrašnjosti i spoljašnjosti trougla. Pod otvorenim trouglom podrazumevaćemo samo njegovu unutrašnjost, a pod zatvorenim trouglom uniju trougla (njegovih temena i stranica) sa njegovom unutrašnjošću. U nekim problemima (na primer, proveri pripadnosti tačke trouglu) je veoma važno razlikovati otvorene i zatvorene trouglove i tada ćemo jasno naglašavati sa kakvim likom radimo, dok je u nekim problemima to irelevantno (na primer, za izračunavanje površine trougla).
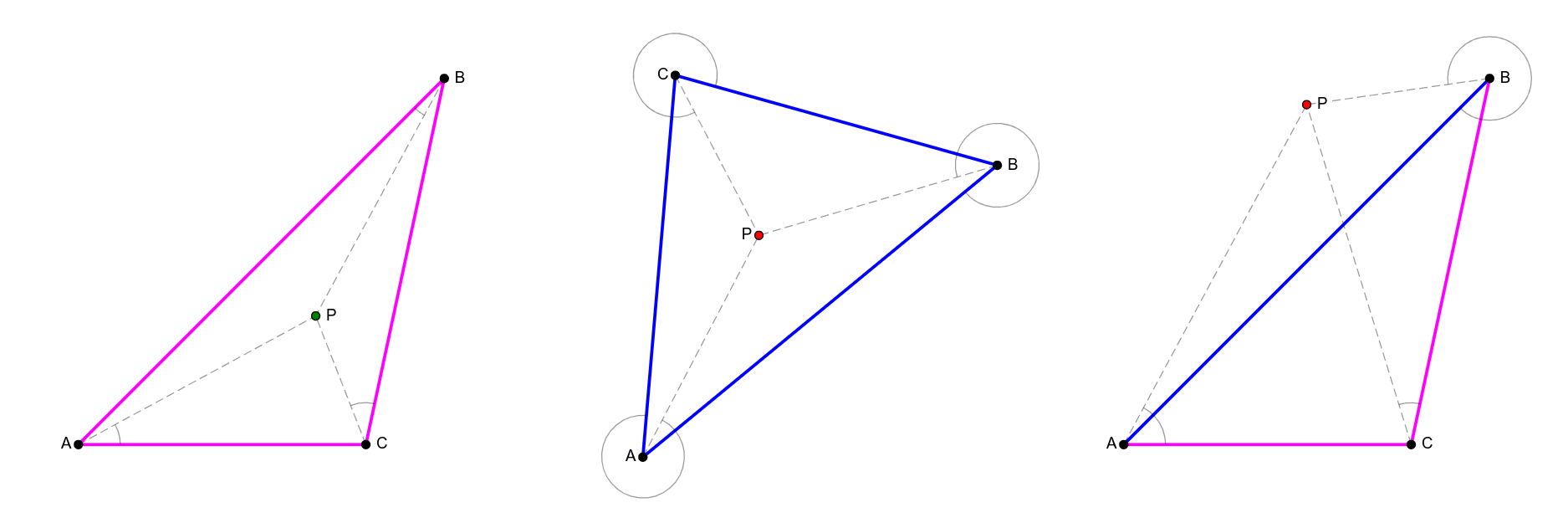
Tačka pripada unutrašnjosti trougla ako i samo ako su tačke \(C\) i \(P\) sa iste strane prave \(AB\), tačke \(A\) i \(P\) sa iste strane prave \(BC\) i tačke \(B\) i \(P\) sa iste strane prave \(CA\). Ako to važi, tada je ista orijentacija trojki \(ABC\) i \(ABP\), ista orijentacija trojki \(BCA\) i \(BCP\) i trojki \(CAB\) i \(CAP\). Pošto su orijentacije trojki \(ABC\), \(BCA\) i \(CAB\) jednake, jednake su i orijentacije trojki \(ABP\), \(BCP\) i \(CAP\). Pokazuje se da je ovo dovoljan uslov da bi tačka \(P\) pripadala otvorenom trouglu \(ABC\) (slika 12).
Obratimo pažnju da ovaj uslov ne obuhvata pripadnost stranicama trougla: naime, ako bi tačka pripadala nekoj stranici, neka orijentacija bi bila jednaka nuli i ne bi bilo moguće da su sve orijentacije međusobno jednake.
U narednom apletu implementirana je provera da li tačka \(P\) pripada unutrašnjosti trougla \(ABC\). Stranice trougla se boje drugačije u zavisnosti od toga sa koje njihove strane se nalazi tačka \(P\) tj.
kakva je odgovarajuća orijentacija. Tačka pripada unutrašnjosti trougla kada se poklopi orijentacija svih trojki \(ABP\), \(BCP\) i \(CAP\).
Kada imamo funkciju za izračunavanje orijentacije na raspolaganju, implementacija provere da li tačka pripada otvorenom trouglu je veoma jednostavna.
bool tackaUOtvorenomTrouglu(const Tacka& T,
const Tacka& A, const Tacka& B, const Tacka& C) {
Orijentacija o1 = orijentacija(A, B, T);
Orijentacija o2 = orijentacija(B, C, T);
Orijentacija o3 = orijentacija(C, A, T);
return o1 == o2 && o2 == o3;
}# include <iostream> {.unnumbered .unlisted}
# include <cmath> {.unnumbered .unlisted}
using namespace std;
// tolerancija
const double EPS = 1e-6;
// tacka je zadata svojim dvema koordinatama
struct Tacka {
double x, y;
Tacka(double x_, double y_) {
x = x_; y = y_;
}
};
// moguce orijentacije trojke tacaka
enum Orijentacija {POZITIVNA, KOLINEARNE, NEGATIVNA};
Orijentacija orijentacija(const Tacka& A, const Tacka& B, const Tacka& C) {
double d = (B.x-A.x)*(C.y-A.y) - (C.x-A.x)*(B.y-A.y);
if (abs(d) < EPS)
return KOLINEARNE;
else if (d > EPS)
return POZITIVNA;
else
return NEGATIVNA;
}
bool tackaUOtvorenomTrouglu(const Tacka& T,
const Tacka& A, const Tacka& B, const Tacka& C) {
Orijentacija o1 = orijentacija(A, B, T);
Orijentacija o2 = orijentacija(B, C, T);
Orijentacija o3 = orijentacija(C, A, T);
return o1 == o2 && o2 == o3;
}
int main() {
double x, y;
cin >> x >> y;
Tacka P(x, y);
cin >> x >> y;
Tacka A(x, y);
cin >> x >> y;
Tacka B(x, y);
cin >> x >> y;
Tacka C(x, y);
if (tackaUOtvorenomTrouglu(P, A, B, C))
cout << "da" << endl;
else
cout << "ne" << endl;
return 0;
}Funkcija za proveru da li tačka pripada zatvorenom trouglu treba da uzme u obzir i da li tačka pripada stranicama trougla u slučaju kada je neka orijentacija nula.
bool tackaUZatvorenomTrouglu(const Tacka& T,
const Tacka& A, const Tacka& B, const Tacka& C) {
Orijentacija o1 = orijentacija(A, B, T);
Orijentacija o2 = orijentacija(B, C, T);
Orijentacija o3 = orijentacija(C, A, T);
if (o1 == 0 && pripadaDuzi(A, B, T)) return true;
if (o2 == 0 && pripadaDuzi(B, C, T)) return true;
if (o3 == 0 && pripadaDuzi(C, A, T)) return true;
return o1 == o2 && o2 == o3;
}Funkcija koja proverava pripadnost tačke duži je prikazana u poglavlju 28. Pošto se ta provera vrši samo kada se već zna da su odgovarajuće tačke kolinearne (jer je orijentacija \(0\)), dovoljno je samo proveriti projekcije na \(x\) i na \(y\)-osu.
Još jedan pristup proveri da li tačka pripada zatvorenom trouglu je da se proveri da li je zbir površina trouglova \(ABP\), \(BCP\) i \(CAP\) jednak površini trougla \(ABC\). Ovaj pristup može biti računski neefikasniji (naročito ako se površine računaju Heronovim obrascem, koji uključuje korenovanje). Dodatno, ako su tačke predstavljene realnim koordinatama, ovaj pristup može da bude numerički nestabilan. Naime, i za tačku koja je unutar trougla, može da se desi da zbir površina tri manja trougla ne bude tačno jednak, već samo blizak površini većeg trougla. Zato je jednakost potrebno proveravati do na neku tačnost \(\varepsilon\) (pri čemu ostaje osetljivo pitanje kako odrediti tu vrednost \(\varepsilon\)). Iz svih navedenih razloga, ovaj pristup je poželjno izbegavati.
bool tackaUZatvorenomTrouglu(const Tacka& T,
const Tacka& A, const Tacka& B, const Tacka& C) {
// racunamo povrsinu trougla ABC
double P = povrsinaTrougla(A, B, C);
// racunamo povrsine trouglova TBC, TAC i TAB
double PA = povrsinaTrougla(T, B, C);
double PB = povrsinaTrougla(A, T, C);
double PC = povrsinaTrougla(A, B, T);
// proveravamo da li one u zbiru daju povrsinu trougla ABC
// poredimo dve realne vrednosti na jednakost
return abs(P - (PA + PB + PC)) < EPS;
}# include <iostream> {.unnumbered .unlisted}
# include <cmath> {.unnumbered .unlisted}
using namespace std;
// tolerancija
const double EPS = 1e-6;
// tacka je zadata svojim dvema koordinatama
struct Tacka {
double x, y;
Tacka(double x_, double y_) {
x = x_; y = y_;
}
};
double povrsinaTrougla(const Tacka& A, const Tacka& B, const Tacka& C) {
// pertle (cik-cak)
return abs(+ A.x*B.y + B.x*C.y + C.x*A.y
- A.x*C.y - C.x*B.y - B.x*A.y) / 2.0;
}
bool tackaUZatvorenomTrouglu(const Tacka& T,
const Tacka& A, const Tacka& B, const Tacka& C) {
// racunamo povrsinu trougla ABC
double P = povrsinaTrougla(A, B, C);
// racunamo povrsine trouglova TBC, TAC i TAB
double PA = povrsinaTrougla(T, B, C);
double PB = povrsinaTrougla(A, T, C);
double PC = povrsinaTrougla(A, B, T);
// proveravamo da li one u zbiru daju povrsinu trougla ABC
// poredimo dve realne vrednosti na jednakost
return abs(P - (PA + PB + PC)) < EPS;
}
int main() {
double x, y;
cin >> x >> y;
Tacka P(x, y);
cin >> x >> y;
Tacka A(x, y);
cin >> x >> y;
Tacka B(x, y);
cin >> x >> y;
Tacka C(x, y);
if (tackaUZatvorenomTrouglu(P, A, B, C))
cout << "da" << endl;
else
cout << "ne" << endl;
return 0;
}Problem. Za duži \(AB\) i \(CD\) zadate koordinatama tačaka \(A\), \(B\), \(C\) i \(D\) odrediti da li se seku i, ako se seku, odrediti bar jednu presečnu tačku. Pretpostaviti da su duži zatvorene, tj. da sadrže svoje krajnje tačke.
Ako su sve tačke u opštem položaju, tj. sve tačke su različite i nikoje tri nisu kolinearne, duži se seku ako i samo ako duž \(AB\) seče pravu \(CD\) i duž \(CD\) seče pravu \(AB\), pa se ispitivanje preseka dve duži može lako svesti na ispitivanje preseka duži i prave (što je opisano u poglavlju 31). Duž seče pravu ako i samo ako su njene krajnje tačke sa raznih strana te prave, a to je problem koji se lako rešava pomoću ispitivanja orijentacije tačaka. Dovoljno je proveriti da li su orijentacije trojki \(CDA\) i \(CDB\) različitog znaka i da li su orijentacije trojki \(ABC\) i \(ABD\) različitog znaka, tj. da li im je proizvod negativan (pri čemu se za orijentaciju trojke \(XYZ\) može uzeti znak dvodimenzionalnog vektorskog proizvoda \(\overrightarrow{XY} \times_{2d} \overrightarrow{XZ}\)). Ovaj test se lako prilagođava slučajevima u kojima su neke tri tačke kolinearne. Naime, umesto da se zahteva da su dve tačke sa striktno različitih strana prave, moguće je uključiti i slučaj da neka od njih pripada pravoj, što se svodi na ispitivanje da li je orijentacija nepozitivna (vrednost joj je manja ili jednaka od nule).
Problem predstavlja degenerisani slučaj kada su sve četiri tačke kolinearne. Naime, ako su sve tačke kolinearne, sve orijentacije trojki biće jednake \(0\) i iz toga nećemo moći da izvučemo nikakav zaključak o međusobnom odnosu dve duži (znamo da one pripadaju jednoj pravoj, ali su svi njihovi međusobni odnosi mogući). U tom slučaju njihov odnos je moguće ispitati ispitivanjem njihovih projekcija na \(x\)-osu (tj. njihovih \(x\)-koordinata). Nažalost, ni ovo nije dovoljno u slučaju kada sve četiri tačke imaju istu \(x\) koordinatu, no tada možemo ispitati njihove projekcije na \(y\)-osu (tj. njihove \(y\)-koordinate). Da bi se projekcije na \(x\)-osu \([a_x, b_x]\) i \([c_x, d_x]\) sekle dovoljno je da ne važi da je jedan od intervala levo od drugog tj. ne sme da važi \(b_x < c_x\) niti \(d_x < a_x\), što je ekvivalentno tome da je \(b_x \geq c_x \wedge d_x \geq a_x\). Prilikom primene ovoga uslova potrebno je obezbediti da se zna šta je levi, a šta desni kraj intervala tj. da je \(a_x \leq b_x\) i \(c_x \leq d_x\). Analogno se postavlja uslov koji mora da važi i za projekcije na \(y\)-osu.
U narednom apletu vrši se provera postojanja preseka duži \(AB\) i \(CD\).
Sledi implementacija provere da li se dve duži seku. Funkcija koja izračunava orijentaciju vraća vrednosti \(-1\), \(0\), \(1\), čime je kôd možda malo manje čitljiv, ali je omogućeno da se provera da li su dva broja istog znaka izvrši tako što se proveri da li je proizvod dve orijentacije nenegativan. Obratimo pažnju na to da umesto vrednosti vektorskog proizvoda funkcija vraća njen znak, čime se izbegava opasnost od prekoračenja prilikom množenja dve orijentacije.
struct Tacka {
int x, y;
};
// 1 za pozitivne vrednosti, -1 za negativne i 0 za nulu
int znak(long long x) {
return (x > 0) - (x < 0);
}
// orijentacija tj. znak vektorskog proizvoda AB x AC
int orijentacija(const Tacka& A, const Tacka& B, const Tacka& C) {
return znak((B.x - A.x) * (C.y - A.y) - (C.x - A.x) * (B.y - A.y));
}
// provera da li prava AB sece duz MN
bool pravaSeceDuz(const Tacka& A, const Tacka& B,
const Tacka& M, const Tacka& N) {
return orijentacija(A, B, M) * orijentacija(A, B, N) <= 0;
}
// provera da li se intervali realne prave [a, b] i [c, d] seku
// (pri cemu se ne zna odnos vrednosti a i b tj. c i d)
bool projekcijeSeSeku(long long a, long long b, long long c, long long d) {
return max(a, b) >= min(c, d) && max(c, d) >= min(a, b);
}
// provera da li se duzi AB i CD seku
bool duziSeSeku(const Tacka& A, const Tacka& B,
const Tacka& C, const Tacka& D) {
return pravaSeceDuz(A, B, C, D) &&
pravaSeceDuz(C, D, A, B) &&
// seku se projekcije na x osu
projekcijeSeSeku(A.x, B.x, C.x, D.x) &&
// seku se projekcije na y osu
projekcijeSeSeku(A.y, B.y, C.y, D.y);
}# include <iostream> {.unnumbered .unlisted}
using namespace std;
struct Tacka {
int x, y;
};
// 1 za pozitivne vrednosti, -1 za negativne i 0 za nulu
int znak(long long x) {
return (x > 0) - (x < 0);
}
// orijentacija tj. znak vektorskog proizvoda AB x AC
int orijentacija(const Tacka& A, const Tacka& B, const Tacka& C) {
return znak((B.x - A.x) * (C.y - A.y) - (C.x - A.x) * (B.y - A.y));
}
// provera da li prava AB sece duz MN
bool pravaSeceDuz(const Tacka& A, const Tacka& B,
const Tacka& M, const Tacka& N) {
return orijentacija(A, B, M) * orijentacija(A, B, N) <= 0;
}
// provera da li se intervali realne prave [a, b] i [c, d] seku
// (pri cemu se ne zna odnos vrednosti a i b tj. c i d)
bool projekcijeSeSeku(long long a, long long b, long long c, long long d) {
return max(a, b) >= min(c, d) && max(c, d) >= min(a, b);
}
// provera da li se duzi AB i CD seku
bool duziSeSeku(const Tacka& A, const Tacka& B,
const Tacka& C, const Tacka& D) {
return pravaSeceDuz(A, B, C, D) &&
pravaSeceDuz(C, D, A, B) &&
// seku se projekcije na x osu
projekcijeSeSeku(A.x, B.x, C.x, D.x) &&
// seku se projekcije na y osu
projekcijeSeSeku(A.y, B.y, C.y, D.y);
}
int main() {
Tacka A, B, C, D;
cin >> A.x >> A.y >> B.x >> B.y >> C.x >> C.y >> D.x >> D.y;
cout << (duziSeSeku(A, B, C, D) ? "da" : "ne") << endl;
return 0;
}Funkcija koju smo implementirali ispravno radi u svim slučajevima (i nedegenerisanim i degenerisanim), ali u mnogim slučajevima vrši neke nepotrebne provere uslova (na primer, ako nisu sve četiri tačke kolinearne, nema potrebe proveravati projekcije na ose). Uz to, nakon što se detektuje da presek postoji, potrebno je izračunati ga sasvim iznova. Prikažimo sada drugačiji metod, koji je malo efikasniji i kojim se može odmah odrediti i presečna tačka.
Na početku računamo \(\overrightarrow{AB}\times_{2d} \overrightarrow{CD}\) i proveravamo da li je taj broj različit od nule. Time smo efektivno ispitali da li su vektori \(\overrightarrow{AB}\) i \(\overrightarrow{CD}\) kolinearni.
Ako je \(\overrightarrow{AB}\times_{2d} \overrightarrow{CD} \neq 0\), u pitanju je nedegenerisani slučaj i ispitujemo da li postoji presečna tačka prave \(AB\) i duži \(CD\), kao i da li postoji presečna tačka prave \(CD\) i duži \(AB\), što možemo uraditi na način koji je opisan u poglavlju 31. Pošto smo vrednost \(\overrightarrow{AB}\times_{2d} \overrightarrow{CD}\), već izračunali, dovoljno je da se izračunaju još samo vrednosti \(\overrightarrow{AC}\times_{2d}\overrightarrow{CD}\) i \(\overrightarrow{AB}\times_{2d}\overrightarrow{CA}\). Primetimo da je potrebno izračunati vrednosti samo \(3\) dvodimenzionalna vektorska proizvoda.
Ako je \(\overrightarrow{AB}\times_{2d} \overrightarrow{CD} = 0\), u pitanju je degenerisani slučaj. Ako tačke \(A\), \(B\) i \(C\) nisu kolinearne, tj. ako je \(\overrightarrow{AB}\times_{2d}\overrightarrow{AC} \neq 0\), tada su prave \(AB\) i \(CD\) paralelne i presek ne postoji. U suprotnom su sve ćetiri tačke kolinearne i potrebno je ispitati projekcije na \(x\)-osu, osim u slučaju kada su sve na vertikalnoj pravoj, kada možemo ispitati projekcije na \(y\)-osu.
// z koordinata vektorskog proizvoda vektora MN i PQ
long long vektorski_proizvod_2d(const Tacka& M, const Tacka& N,
const Tacka& P, const Tacka& Q) {
return (N.x - M.x)*(Q.y - P.y) - (N.y - M.y)*(Q.x - P.x);
}
// provera da li je 0 <= brojilac/imenilac <= 1
bool kolicnikUIntervalu01(int brojilac, int imenilac) {
return brojilac == 0 ||
(istogZnaka(brojilac, imenilac) && abs(brojilac) <= abs(imenilac));
}
// provera da li se intervali realne prave [a, b] i [c, d] seku
// (pri cemu se ne zna odnos vrednosti a i b tj. c i d)
bool projekcijeSeSeku(long long a, long long b, long long c, long long d) {
return max(a, b) >= min(c, d) && max(c, d) >= min(a, b);
}
// provera da li se duzi AB i CD seku
bool duziSeSeku(const Tacka& A, const Tacka& B,
const Tacka& C, const Tacka& D) {
int ABCD = vektorski_proizvod_2d(A, B, C, D);
if (ABCD != 0) {
int ABCA = vektorski_proizvod_2d(A, B, C, A);
int ACCD = vektorski_proizvod_2d(A, C, C, D);
// presecna tacka se moze odrediti kao: C + (ABCA/ABCD)CD
return kolicnikUIntervalu01(ACCD, ABCD) &&
kolicnikUIntervalu01(ABCA, ABCD);
} else {
int ABAC = vektorski_proizvod_2d(A, B, A, C);
if (ABAC != 0)
return false;
if (A.x == B.x && C.x == D.x)
return projekcijeSeSeku(A.y, B.y, C.y, D.y);
else
return projekcijeSeSeku(A.x, B.x, C.x, D.x);
}
}# include <iostream> {.unnumbered .unlisted}
using namespace std;
struct Tacka {
int x, y;
};
// provera da li su brojevi m i n (n je razlicito od nule) istog znaka
bool istogZnaka(int m, int n) {
return (m > 0) == (n > 0);
}
// z koordinata vektorskog proizvoda vektora MN i PQ
long long vektorski_proizvod_2d(const Tacka& M, const Tacka& N,
const Tacka& P, const Tacka& Q) {
return (N.x - M.x)*(Q.y - P.y) - (N.y - M.y)*(Q.x - P.x);
}
// provera da li je 0 <= brojilac/imenilac <= 1
bool kolicnikUIntervalu01(int brojilac, int imenilac) {
return brojilac == 0 ||
(istogZnaka(brojilac, imenilac) && abs(brojilac) <= abs(imenilac));
}
// provera da li se intervali realne prave [a, b] i [c, d] seku
// (pri cemu se ne zna odnos vrednosti a i b tj. c i d)
bool projekcijeSeSeku(long long a, long long b, long long c, long long d) {
return max(a, b) >= min(c, d) && max(c, d) >= min(a, b);
}
// provera da li se duzi AB i CD seku
bool duziSeSeku(const Tacka& A, const Tacka& B,
const Tacka& C, const Tacka& D) {
int ABCD = vektorski_proizvod_2d(A, B, C, D);
if (ABCD != 0) {
int ABCA = vektorski_proizvod_2d(A, B, C, A);
int ACCD = vektorski_proizvod_2d(A, C, C, D);
// presecna tacka se moze odrediti kao: C + (ABCA/ABCD)CD
return kolicnikUIntervalu01(ACCD, ABCD) &&
kolicnikUIntervalu01(ABCA, ABCD);
} else {
int ABAC = vektorski_proizvod_2d(A, B, A, C);
if (ABAC != 0)
return false;
if (A.x == B.x && C.x == D.x)
return projekcijeSeSeku(A.y, B.y, C.y, D.y);
else
return projekcijeSeSeku(A.x, B.x, C.x, D.x);
}
}
int main() {
Tacka A, B, C, D;
cin >> A.x >> A.y >> B.x >> B.y >> C.x >> C.y >> D.x >> D.y;
cout << (duziSeSeku(A, B, C, D) ? "da" : "ne") << endl;
return 0;
}Prethodni program je veoma jednostavno preraditi tako da izračunava i presečnu tačku duži ako ona postoji.
Treće moguće rešenje bi bilo da za tačke \(A\) i \(B\) ispitamo da li pripadaju duži \(CD\), a za tačke \(C\) i \(D\) da li pripadaju duži \(AB\) (ako je bilo šta od ovoga zadovoljeno, duži se seku). Da bi se ispitalo da li tačka \(P\) pripada duži \(MN\) dovoljno je proveriti da li su tačke \(M\), \(N\) i \(P\) kolinearne (tj. da li je orijentacija trojke \(MNP\) jednaka nuli) i da li je \(x\)-koordinata tačke \(P\) između \(x\)-koordinata tačaka \(M\) i \(N\) kao i da li je \(y\)-koordinata tačke \(P\) između \(y\)-koordinata tačaka \(M\) i \(N\).
Objekti koji se često razmatraju u računarskoj geometriji su i mnogouglovi.
Put \(P\) je niz tačaka \(P_1\), \(P_2,\ldots,P_k\) i duži \(P_1P_2\), \(P_2P_3,\ldots,P_{k-1}P_k\) koje ih povezuju. Duži koje čine put su njegove stranice (ivice). Primetimo da je u opštem slučaju dopušteno da tačke na putu budu i kolinearne.
Zatvoreni put je put čija se poslednja tačka poklapa sa prvom i nazivamo ga mnogougao ili poligon. Tačke koje definišu mnogougao su njegova temena.
Na primer, trougao je mnogougao sa tri temena. Mnogougao se predstavlja nizom, a ne skupom tačaka, jer je bitan redosled kojim se tačke zadaju; promenom redosleda tačaka iz istog skupa u opštem slučaju dobija se drugi mnogougao.
Prost mnogougao je onaj kod koga odgovarajući put nema preseka sa samim sobom; drugim rečima, jedine stranice koje imaju zajedničke tačke su susedne stranice sa svojim zajedničkim temenom. Prost mnogougao deli ravan na dve oblasti: unutrašnjost i spoljašnost. Na slici 13, levo prikazan je jedan prost mnogougao, dok je na sredini prikazan jedan mnogougao koji nije prost (tj. mnogougao koji je samopresecajući).

Otvoren mnogougao sadrži samo tačke u unutrašnjosti mnogougla (bez tačaka na stranicama). Zatvoren mnogougao pored tačaka u unutrašnjosti sadrži i tačke na stranicama mnogougla.
Konveksni mnogougao je mnogougao čija unutrašnjost sa svake dve tačke koje sadrži, sadrži i sve tačke duži koje te tačke određuju (ekvivalentno, mnogougao je konveksan ako su mu svi unutrašnji uglovi manji ili jednaki \(180^\circ\) tj. \(\pi\) radijana). Konveksni put je put sastavljen od tačaka \(P_1\), \(P_2,\ldots,P_k\) takav da je mnogougao \(P_1P_2\ldots P_k\) konveksan. Mnogougao na slici 13 levo je konveksan, dok je mnogougao na toj slici desno nekonveksan.
U narednom apletu možete videti kada je mnogougao prost, konveksan (tada je obojen plavom bojom), prost, nekonveksan (tada je obojen zelenom bojom) ili samopresecajući (tada je obojen crvenom bojom).
Prirodno se postavlja pitanje ispitivanja da li je mnogougao zadat nizom svojih tačaka prost i da li je konveksan.
Ispitivanje da li je dati poligon prost grubom silom podrazumeva da se proveri postojanje preseka svakog para stranica. Problem ispitivanja preseka duži je opisan u poglavlju 33 i provera da li se dve duži seku se može izvršiti u vremenu \(O(1)\), međutim, mnogougao sa \(n\) temena ima \(n\) stranica i \(\frac{n(n+1)}{2}\) parova stranica, pa je složenost ovog algoritma \(O(n^2)\).
Postoje i efikasniji načini da se ovaj problem reši. Bentli-Otmanov4 algoritam pronalazi sve preseke koji postoje u skupu od \(n\) duži u vremenu \(O((n+k)\log{n})\), gde je \(k\) broj preseka koji postoje (ovaj algoritam ima izlazno zavisnu složenost). Ako je broj preseka \(k\) znatno mali (što je čest slučaj), složenost je značajno bolja od algoritma grube sile. Opis ovog algoritma prevazilazi okvire ovog udžbenika. Ipak, u poglavlju 34 opisaćemo jednostavniju varijantu u kojoj se zna da su duži čiji se preseci traže horizontalne ili vertikalne. Da bi se proverilo da li je mnogougao prost, Bentli-Otmanov algoritam se primenjuje na skup svih stranica mnogougla. Ako preseka nema, složenost ispitivanja će biti \(O(n\log{n})\), a ako postoje preseci, algoritam može da se zustavi već nakon nalaženja prvog preseka, što opet garantuje složenost \(O(n\log{n})\), čak i kada preseka postoji puno.
U prostom konveksnom mnogouglu su sve trojke tačaka \(P_iP_jP_k\) za \(0 \leq i < j < k < n\) isto orijentisane. To je i dovoljan uslov da bi mnogougao bio prost i konveksan. Algoritmom grube sile bi se izračunale i uporedile sve ove orijentacije, što se može uraditi u vremenu \(O(n^3)\) (jer toliko trojki postoji) i veoma je neefikasno.
U konveksnom mnogouglu sve trojke uzastopnih tačaka imaju istu orijentaciju (na primer, kada se tačke obilaze redom, do naredne tačke se uvek dolazi praveći levi zaokret tj. zaokret u pozitivnom smeru), tj. sve trojke \(P_iP_{i+1}P_{i+2}\) za \(0 \leq i < n\) i \(P_n=P_0\), \(P_{n+1}=P_1\) imaju istu orijentaciju. Ovaj uslov nije dovoljan da bi mnogougao bio konveksan. Na primer, pentagram (zvezda petokraka) zadovoljava ovaj uslov, svi uglovi su oštri, ali ona nije konveksan mnogougao – nije čak ni prost, jer se nesusedne stranice seku. Ipak, ako se unapred zna da je mnogougao prost, ovaj uslov je dovoljan i da bi bio konveksan i može se koristiti kao algoritam za proveru, čija je složenost \(O(n)\).
Slično kao što je u poglavlju 29 pokazano za trougao, i mnogougao se može rastaviti na trapeze, tako da se označena površina prostog mnogougla može dobiti sabiranjem označenih površina pojedinačnih trapeza. Transformacijom tako dobijene formule dobija se ponovo formula pertle kojom se izračunava površina prostog mnogougla čija su temena tačke sa koordinatama \((x_1, y_1)\), \((x_2, y_2)\), \(\ldots\), \((x_n, y_n)\).
\[P = \frac{1}{2}\sum_{i=1}^{n}\left(x_iy_{i+1} - x_{i+1}y_i\right)\]
Pri tom se podrazumeva da je \((x_{n+1}, y_{n+1}) = (x_1, y_1)\).
Slika je preuzeta sa Vikipedije ().↩︎
Pojam vektorskog proizvoda (engl. cross product) se u teorijskom matematici uopštava i na \(n\)-dimenzionalne vektorske prostore, međutim, prikazana definicija dvodimenzionalnog vektorskog proizvoda se ne uklapa u tu opštu definiciju. Vrednost \(a\times_{2d} b\) se nekada naziva i označena površina (engl. signed area) paralelograma određenog preko vektorima \(a\) i \(b\) u ravni. U tom svetlu, ona je analogna operaciji mešovitog proizvoda trodimenzionalnih vektora, kojom se računa označena zapremina paralelepipeda kog tri vektora grade. Vrednost \(a\times_{2d} b\) se nekada naziva i normalni skalarni proizvod (engl. perp dot product), jer je \(a\times_{2d} b = a^\perp \circ b\), gde je sa \(a^\perp\) označen vektor normalan na \(a\), dobijen rotacijom vektora \(a\) za 90 stepeni. Ipak termin vektorski proizvod (engl. cross product) je zastupljen u literaturi o geometrijskim algoritmima i računarskoj grafici, pa ćemo ga i mi koristiti.↩︎
Aksiomatsko zasnivanje orijentacije detaljno je opisano u knjizi Donada Knuta “Aksiome i omotači”.↩︎
Algoritam su 1979. godine opisali Džon Bentli (engl. Jon Bentley) i Tomas Otman (engl. Thomas Ottmann), američki informatičari.↩︎