Ako su \(a\) i \(b\) celi brojevi i važi \(b\neq 0\), kažemo da je broj \(q\) količnik, a broj \(r\) ostatak pri deljenju broja \(a\) brojem \(b\) ako i samo ako važi \(a = q\cdot b + r\) i \(0 \leq r < y\). Brojevi \(q\) i \(r\) su ovim uslovom jedinstveno određeni. Pisaćemo \(q = a \,\mathrm{div}\,b\) i \(r = a \,\mathrm{mod}\,b\). U programskim jezicima se operacija \(\,\mathrm{mod}\,\) obično označava simbolom %, dok je \(\,\mathrm{div}\,\) celobrojno deljenje uz zaokruživanje naniže (što je podrazumevano ponašanje operatora / primenjenog na cele brojeve), odnosno \(a \,\mathrm{div}\,b = \left\lfloor{\frac{a}{b}}\right\rfloor\). Neki programski jezici imaju poseban operator za izračunavanje celobrojnog količnika (npr. operator // u jeziku Python). Treba biti obazriv jer različiti programski jezici drugačije tretiraju slučajeve kada je neki od brojeva \(a\) ili \(b\) negativan (u nekim jezicima operator % izračunava pozitivan, a u nekim negativan ostatak, što je u suprotnosti sa definicijom ostatka koju smo naveli).
Broj \(a\) je deljiv brojem \(b \neq 0\), što označavamo \(b\vert a\), ako i samo ako je \(a \,\mathrm{mod}\,b = 0\). Broj \(b\) je delilac broja \(a\), a broj \(a\) je sadržalac broja \(b\).
Brojevi koji imaju tačno dva različita delioca nazivaju se prosti – \(n > 1\) je prost ako su mu jedini delioci \(1\) i \(n\). Prirodni brojevi koji imaju više od dva različita delioca su složeni. Broj \(1\) nije ni prost ni složen. Prostih brojeva ima beskonačno mnogo. Naime, ako pretpostavimo da ih ima konačno mnogo, broj koji bi se dobio množenjem svih prostih brojeva i dodavanjem broja \(1\) na taj proizvod bio bi veći od svih prostih brojeva, a ne bi bio deljiv nijednim od njih, te bi morao da bude prost, čime bismo dobili kontradikciju. Svi brojevi manji od datog broja \(n\) se mogu efikasno odrediti algoritmom poznatim pod imenom Eratostenovo sito.
Najveći zajednički delilac (NZD) brojeva \(a\) i \(b\) je najveći broj \(d\) takav da \(d\vert a\) i \(d \vert b\), a najmanji zajednički sadržalac (NZS) brojeva \(a\) i \(b\) je najmanji broj \(s\) takav da \(a\vert s\) i \(b\vert s\). Podsetimo se osnovnog Euklidovog algoritma za određivanje najvećeg zajedničkog delioca brojeva \(a\) i \(b\).
Razmotrimo problem pronalaženja NZD dva broja.
Problem. Za date nenegativne cele brojeve \(a\) i \(b\) koji nisu istovremeno jednaki nuli izračunati \(\mathrm{nzd}(a, b)\).
Razmatramo čuveni Euklidov algoritam. Algoritam se može ilustrovati i geometrijski i u direktnoj je vezi sa problemom određivanja maksimalne dimenzije jednakih kvadrata kojima može da se poploča pravougaonik čije su dužine stranica \(a\) i \(b\).
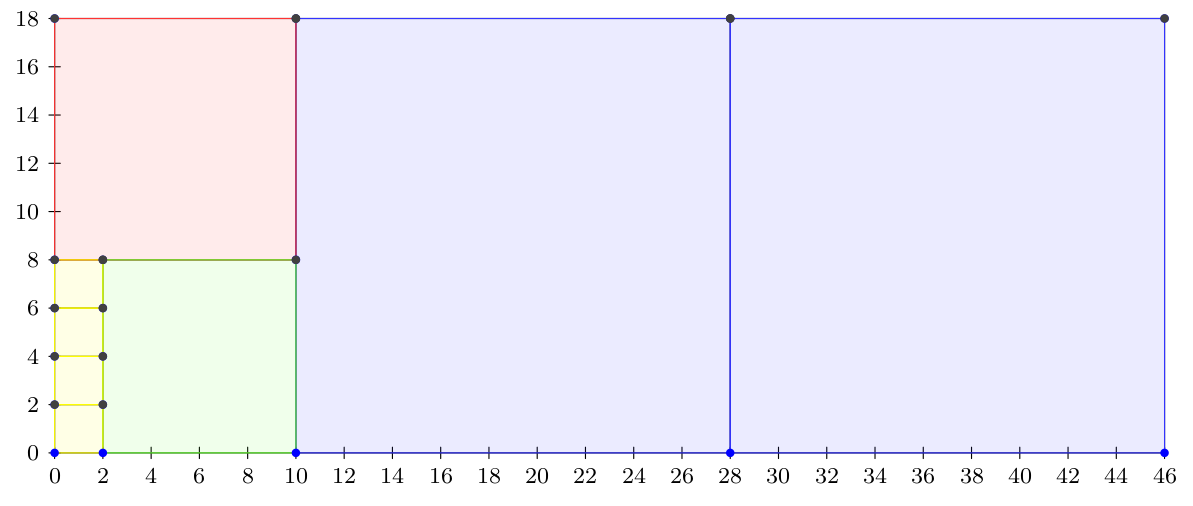
Primer 3.1.1. Neka je dat pravougaonik dimenzije \(a = 46\) i \(b = 18\), prikazan na slici 1. Tada se prvo iz njega mogu iseći dva kvadrata dimenzije \(18\times 18\) i ostaje nam pravougaonik dimenzije \(18\times 10\). Ukoliko nekim manjim kvadratima uspemo da popločamo taj preostali pravougaonik, tim kvadratima ćemo moći da popločamo i ove kvadrate dimenzije \(18\times 18\) (jer će dimenzija tih malih kvadrata deliti broj \(18\) jednak jednoj dimenziji preostalog pravougaonika), pa ćemo samim tim moći da popločamo i ceo polazni pravougaonik dimenzija \(46\times 18\). Od pravougaonika dimenzije \(18\times 10\) možemo iseći kvadrat dimenzije \(10\times 10\) i preostaje nam pravougaonik dimenzije \(10\times 8\). Ponovo, kvadratići kojima se može popločati taj preostali pravougaonik biće takvi da se njima može popločati i isečeni kvadrat dimenzije \(10\times 10\). Od tog pravougaonika isecamo kvadrat dimenzije \(8\times 8\) i dobijamo pravougaonik dimenzije \(8\times 2\). Njega možemo razložiti na četiri kvadrata dimenzije \(2\times 2\) i to je najveća dimenzija kvadrata kojima se može popločati polazni pravougaonik.

Implementacija koja direktno prati prethodnu definiciju je rekurzivna, a moguće je jednostavno napraviti i iterativnu implementaciju, u kojoj se u svakom koraku vrednost većeg od dva broja zamenjuje njihovom razlikom, sve dok se brojevi ne izjednače.
Rekurzivno se algoritam može izraziti na sledeći način.
int nzd(int a, int b) {
if (a > b) return nzd(a-b, b);
if (a < b) return nzd(a, b-a);
return a;
}Rekurzija se iz prethodnog algoritma može jako lako ukloniti.
int nzd(int a, int b) {
while (a != b) {
if (a > b)
a -= b;
else
b -= a;
}
return a;
}U narednom apletu možete isprobati geometrijski interpretaciju Euklidovog algoritma.
Dokažimo formalno korektnost algoritma (dokazujemo samo korektnost rekurzivne varijante, pošto joj je iterativna varijanta ekvivalentna).
Teorema 3.1.1. [Korektnost Euklidovog algoritma sa oduzimanjem] Za date prirodne brojeve \(a\) i \(b\), koji nisu istovremeno jednaki nuli, Euklidov algoritam sa oduzimanjem korektno izračunava njihov NZD.
Dokaz. Korektnost rekurzivne implementacije se jednostavno može dokazati indukcijom.
Bazu čini slučaj \(a = b\). Pošto su brojevi različiti od nule, očigledno je da je njihov NZD jednak \(a=b\).
Pretpostavimo da je \(a > b\). Tada je \(\mathrm{nzd}(a, b) = \mathrm{nzd}(a, a - b)\). Zaista, ako neki broj \(d\) deli brojeve \(a\) i \(b\), tada on deli i \(a-b\). Dakle, \(d=\mathrm{nzd}(a, b)\) sigurno deli i \(b\) i \(a-b\). Ako on ne bi bio NZD brojeva \(a-b\) i \(b\), tada bi postojao neki veći broj \(d'\) koji bi delio i \(a-b\) i \(b\). Međutim, tada bi \(d'\) delio i zbir \(a = (a-b) + b\), pa bi \(d'\) bio i delilac brojeva \(a\) i \(b\), koji je veći od \(d\), što je kontradikcija sa tim da je \(d\) NZD brojeva \(a\) i \(b\). Na osnovu induktivne hipoteze \(\mathrm{nzd}(a, a - b)\) umemo ispravno da izračunamo.
Slučaj \(a < b\) je potpuno simetričan. \(\Box\)
Ovaj se algoritam lako može optimizovati. Razmotrimo određivanje NZD dva broja na jednom primeru.
Primer 3.1.2. \(\mathrm{nzd}(279, 45)\) = \(\mathrm{nzd}(234, 45)\) = \(\mathrm{nzd}(189, 45)\) = \(\mathrm{nzd}(144, 45)\) = \(\mathrm{nzd}(99, 45)\) = \(\mathrm{nzd}(54, 45)\) = \(\mathrm{nzd}(9, 45)\) = \(\mathrm{nzd}(9, 36)\) = \(\mathrm{nzd}(9, 27)\) = \(\mathrm{nzd}(9, 18)\) = \(\mathrm{nzd}(9, 9)\) = \(9\).
Možemo primetiti dugačak niz koraka u kojima se malo po malo od broja \(279\) oduzima broj \(45\), sve dok se ne dođe do broja koji je manji od broja \(45\). Za tim nema potrebe, jer znamo da će se posle tog dugog niza koraka postupak zaustaviti kada nam jedan argument bude baš \(45\), a drugi bude jednak ostatku pri deljenju broja \(279\) brojem \(45\), a to je broj \(9\). Dakle, umesto da iterativno taj ostatak računamo uzastopnim oduzimanjima, bolji pristup je da primenimo deljenje i u jednom koraku ga izračunamo kao ostatak pri deljenju. Ako sličan princip primenimo na brojeve \(9\) i \(45\), doći ćemo do toga da će nam ostati broj \(9\) i ostatak pri deljenju ta dva broja, što je nula. To nije baš u potpunosti identično kao u slučaju oduzimanja, gde smo se zaustavili kod para \((9, 9)\), međutim, sasvim je ispravno i može se smatrati produženjem prethodnog postupka u kom bi se pre prijavljivanja rezultata uradilo još jedno oduzimanje i došlo se do toga da je jedan od brojeva jednak nuli, kada je NZD jednak drugom broju.
Brži Euklidov algoritam, u kom se koristi deljenje, zasnovan je na sledećim tvrđenjima.
Primetimo da nema potrebe analizirati koji je broj manji, a koji je veći. Ako je \(a < b\), tada važi \(a \,\mathrm{mod}\,b = a\), pa se u prvom koraku dobija da je \(\mathrm{nzd}(a, b) = \mathrm{nzd}(b, a)\). Pošto je \(a \,\mathrm{mod}\,b < b\), jednom kada je prvi argument veći od drugog, to će tako ostati do kraja.
I Euklidov algoritam sa deljenjem, dakle, dopušta jednostavnu rekurzivnu implementaciju.
int nzd(int a, int b) {
if (b == 0)
return a;
return nzd(b, a % b);
}Euklidov algoritam se može formulisati i implementirati i iterativno, tako što u petlji koja se izvršava sve dok je broj \(b\) veći od nule par promenljivih \((a, b)\) zamenjujemo vrednostima \((b, a \,\mathrm{mod}\,b)\). Na kraju petlje je \(b=0\), tako da kao rezultat možemo prijaviti tekuću vrednost broja \(a\).
int nzd(int a, int b) {
while (b != 0) {
int ost = a % b;
a = b;
b = ost;
}
return a;
}U prethodnom apletu možete isprobati i geometrijsku interpretaciju optimizovanog Euklidovog algoritma zasnovanog na deljenju.
Dokažimo formalno korektnost algoritma (dokazujemo samo korektnost rekurzivne varijante, pošto joj je iterativna varijanta ekvivalentna).
Teorema 3.1.2. [Korektnost Euklidovog algoritma sa deljenjem] Za date prirodne brojeve \(a\) i \(b\), koji nisu istovremeno jednaki nuli, Euklidov algoritam sa deljenjem korektno izračunava njihov NZD.
Dokaz. Korektnost rekurzivne varijante se dokazuje matematičkom indukcijom.
Bazu čini slučaj \(\mathrm{nzd}(a, 0)\), za \(a \neq 0\). Pošto važi \(a \vert 0\) i \(a \vert a\), a ne postoji ni jedan broj \(a' > a\) takav da \(a' \vert a\), važi da je \(\mathrm{nzd}(a, 0) = a\).
Na osnovu definicije celobrojnog deljenja važi \(a = (a\,\mathrm{div}\,b)\cdot b + (a \,\mathrm{mod}\,b)\). Obeležimo sa \(d\) NZD brojeva \(b\) i \(a\,\mathrm{mod}\,b\). Da bismo dokazali da je on ujedno NZD brojeva \(a\) i \(b\) dovoljno je dokazati da on deli ta dva broja i da svaki broj koji deli ta dva broja deli njega.
Pošto broj \(d\) deli brojeve \(b\) i \(a \,\mathrm{mod}\,b\), on deli oba sabirka na desnoj strani, pa zato deli i njihov zbir koji je jednak \(a\), te zato deli i \(a\) i \(b\).
Dalje, ako neki broj \(d'\) deli brojeve \(a\) i \(b\), on mora deliti i broj \(a\,\mathrm{mod}\,b\) (jer se on može iskazati kao razlika dva broja deljivih brojem \(d'\)), pa pošto je \(d'\) delilac brojeva \(b\) i \(a\,\mathrm{mod}\,b\), on mora deliti i njihov NZD, tj. mora deliti broj \(d\).
Pošto \(\mathrm{nzd}(b, a \,\mathrm{mod}\,b)\) možemo izračunati na osnovu induktivne hipoteze, tvrđenje je dokazano. \(\Box\)
Euklidov algoritam koji je zasnovan na deljenju možemo predstaviti i na sledeći način:
\[ \begin{array}{rcll} r_0 &=& a\\ r_1 &=& b\\ r_2 &=& r_0 \,\mathrm{mod}\,r_1 = r_0 - q_1r_1, &\quad 0 < r_2 < r_1\\ \ldots\\ r_{i+1} &=& r_{i-1} \,\mathrm{mod}\,r_i = r_{i-1} - q_ir_i, & \quad 0 < r_{i+1} < r_i\\ \ldots \\ r_{k} &=& r_{k-2} \,\mathrm{mod}\,r_{k-1} = r_{k-2} - q_{k-1}r_{k-1}, &\quad 0 < r_k < r_{k-1}\\ r_{k+1} &=& r_{k-1} \,\mathrm{mod}\,r_k = r_{k-1} - q_kr_k, & \quad r_{k+1} = 0 \end{array} \]
Vrednost \(r_k\) je NZD brojeva \(a\) i \(b\). Zaista, pošto je \(r_{k+1}=0\), važi \(r_{k-1} = q_kr_k\), pa broj \(r_k\) deli \(r_{k-1}\). Međutim, pošto je \(r_{k-2} = q_{k-1}r_{k-1} + r_{k}\), \(r_k\) deli i \(r_{k-2}\). Sličnim rezonovanjem, unazad, može se zaključiti da \(r_k\) deli i \(r_1\) i \(r_0\), tj. \(a\) i \(b\). Obratno, ako neki broj deli i \(a\) i \(b\) onda on deli i \(r_0\) i \(r_1\), a pošto je \(r_2 = r_0 - q_1r_1\), on deli i \(r_2\). Sličnim rezonovanjem, unapred, može se zaključiti da taj broj mora deliti i \(r_k\). Stoga je \(r_k\) NZD brojeva \(a\) i \(b\).
Dakle, polazeći od brojeva \(r_0=a\) i \(r_1=b\), izračunava se ostatak \(r_2=r_0\,\mathrm{mod}\,r_1\), zatim ostatak \(r_3=r_1\,\mathrm{mod}\,r_2\), itd. Na taj način dobija se opadajući niz ostataka \(r_i\) za koji važi:
\[r_{i-1}=q_i r_i+r_{i+1},\quad 0\le r_{i+1}<r_i,\text{ za }i=1,2,\ldots,k\](1)
Pri deljenju \(r_{i-1}\) sa \(r_i\) količnik je \(q_i\), a ostatak \(r_{i+1}\). Dobijeni niz \(r_i\) je konačan jer je opadajući (važi \(r_{i+1}<r_i\) za svako \(i\)), a sastoji se od prirodnih brojeva. Ako je \(r_{k+1}=0\) i \(r_k\neq 0\) poslednji član ovog niza različit od nule, kako je
\[\mathrm{nzd}(r_0, r_1)=\mathrm{nzd}(r_1, r_2)=\ldots=\mathrm{nzd}(r_{k-1}, r_{k})=\mathrm{nzd}(r_{k}, 0)=r_k,\]
zaključujemo da je \(d=\mathrm{nzd}(a, b)\) upravo jednako \(r_k\), poslednjem ostatku u nizu ostataka koji je različit od nule.
Upotrebiti naredni aplet da proverite da li ste razumeli kako se određuje niz ostataka \(r_0=a\), \(r_1=b\), \(r_2\), …, \(r_k\), \(r_{k+1}=0\).
Što se tiče implementacije, u svakom koraku algoritma održavamo dve uzastopne vrednosti niza ostataka. U početku, to su članovi \(r_0\) i \(r_1\), tj. originalne vrednosti \(a\) i \(b\). Važi da je \(q_1 = a\,\mathrm{div}\,b\), a \(r_2 = a \,\mathrm{mod}\,b\). U drugom koraku promenljive \(a\) i \(b\) treba da imaju vrednosti članova \(r_1\) i \(r_2\), što znači da se par promenljivih \(a\), \(b\) zamenjuje vrednostima \(b\) i \(a\,\mathrm{mod}\,b\). Postupak se nastavlja sve dok par uzastopnih vrednosti ne postane \(r_k\), \(r_{k+1}\), tj. pošto par uzastopnih vrednosti održavamo u promenljivama \(a\) i \(b\), dok \(b\) ne postane nula i tada je NZD koji je jednak \(r_k\) sadržan u promenljivoj \(a\).
Primetimo da se posle najviše jednog koraka osigurava da je \(a > b\) (jer se u svakom koraku par \((a, b)\) zamenjuje parom \((b, a \,\mathrm{mod}\,b)\), a uvek važi da je \(a \,\mathrm{mod}\,b < b\)). Posle bilo koje dve iteracije se od para \((a, b)\) dolazi do para \((a \,\mathrm{mod}\,b, b \,\mathrm{mod}\,(a \,\mathrm{mod}\,b))\) (naravno, pod pretpostavkom da je \(b \neq 0\) i da je \(a \,\mathrm{mod}\,b \neq 0\)). Dokažimo da je \(a \,\mathrm{mod}\,b < a/2\). Ako je \(b \leq a/2\), tada je \(a \,\mathrm{mod}\,b < b \leq a/2\). U suprotnom, za \(b > a/2\) važi da je \(a \,\mathrm{mod}\,b = a - b < a/2\). Zato se prvi argument posle svaka dva koraka smanjuje bar dvostruko. Do vrednosti \(1\) prvi argument stiže u logaritamskom broju koraka u odnosu na veći od polazna dva broja i tada drugi broj sigurno dostiže nulu (jer je strogo manji od prvog) i postupak se završava. Dakle, složenost algoritma je logaritamska u odnosu na veći od dva broja, odnosno \(O(\log(a + b))\). Ako se složenost računa u odnosu na broj cifara broja (što je veličina ulaza), onda je ona zapravo linearna. Ovo ukazuje na to da je problem određivanja NZD veoma lak problem i da se efikasno može rešiti i za ogromne brojeve (brojeve i sa nekoliko hiljada cifara).
Uz malu dopunu, Euklidov algoritam se može iskoristiti i za rešavanje sledećeg problema.
Problem. Najveći zajednički delilac \(d\) dva prirodna broja \(a\) i \(b\) izraziti kao njihovu celobrojnu linearnu kombinaciju. Drugim rečima, odrediti cele brojeve \(x\) i \(y\), tako da važi \(d=\mathrm{nzd}(a, b)=x\cdot a+y\cdot b.\)
Primer 3.1.3. Najveći zajednički delilac brojeva \(a=10\) i \(b=18\) je \(d=2\) i on se može predstaviti kao njihova celobrojna linearna kombinacija na sledeći način: \(2=2\cdot 10-1\cdot 18\).
Brojevi \(x\) i \(y\) postoje na osnovu tvrđenja koje je poznato kao Bezuov stav, a koje ćemo u nastavku konstruktivno dokazati na dva različita načina (iz kojih će proizaći dva različita algoritma za izračunavanje koeficijenata \(x\) i \(y\)).
Teorema 3.1.3. [Bezuov stav] Ako su \(a\) i \(b\) dva prirodna broja (ne istovremeno jednaka nuli) i važi da je \(\mathrm{nzd}(a, b) = d\), tada postoje celi brojevi \(x\) i \(y\) takvi da je \(x\cdot a + y\cdot b = d\).
Pošto je \(r_0=a\) i \(r_1=b\), problem možemo formulisati nešto drugačije: zadatak je broj \(d=\mathrm{nzd}(a, b)\) izraziti u obliku celobrojne linearne kombinacije ostataka \(r_0\) i \(r_1\), odnosno kao \(d=r_k=x\cdot r_0 + y\cdot r_1\), gde je \(r_k\) poslednji član niza ostataka različit od nule. Ovako formulisan problem se može rešiti indukcijom.
Polazi se od baznog slučaja koji odgovara predstavljanju broja \(d\) kao celobrojne linearne kombinacije dva uzastopna ostatka \(r_{k-2}\) i \(r_{k-1}\): \(d=r_k=r_{k-2}-q_{k-1}r_{k-1}\). Ovaj izraz je ekvivalentan pretposlednjem deljenju u Euklidovom algoritmu (izraz (1)) za \(i=k-1\).
Korak indukcije bio bi da se polazeći od izraza za \(d\) \(d=x'\cdot r_i+y'\cdot r_{i+1}\)(2)
kao celobrojne linearne kombinacije ostataka \(r_{i}\) i \(r_{i+1}\), broj \(d\) izrazi kao celobrojna linearna kombinacija ostataka \(r_{i-1}\) i \(r_{i}\), odnosno u obliku \(d=x''\cdot r_{i-1}+y''\cdot r_{i}.\) Ovo se postiže zamenom vrednosti \(r_{i+1}\) u jednakosti (2) sa \(r_{i-1}-q_{i}r_{i}\) iz jednakosti (1). Na taj način se dobija
\[d = x'\cdot r_i+y'\cdot r_{i+1} = x'\cdot r_i+y'\cdot (r_{i-1}-q_i r_i) = y'\cdot r_{i-1}+(x'-q_i y')\cdot r_i\](3)
odnosno:
\[\begin{eqnarray*} x'' &=& y' \\ y'' &=& x'-q_iy' \end{eqnarray*}\]
tj. izrazili smo \(d\) u obliku celobrojne linearne kombinacije ostataka \(r_{i-1}\) i \(r_{i}\). Dakle, indukcijom po \(i\), \(i=k-2,k-3,\ldots,1\), dokazano je da se \(d\) može izraziti kao celobrojna linearna kombinacija proizvoljna dva uzastopna člana \(r_{i}\) i \(r_{i+1}\) niza ostataka. Specijalno, za \(i=0\), dobija se traženi izraz. Ova verzija Euklidovog algoritma se ponekad naziva prošireni Euklidov algoritam (engl. extended Euclidean algorithm).
Primer 3.1.4. Potrebno je odrediti cele brojeve \(x\) i \(y\) tako da važi \(3=33x+24y\). S obzirom na to da je \(\mathrm{nzd}(33, 24)=3\), možemo iskoristiti prethodni postupak za određivanje brojeva \(x\) i \(y\). Prilikom izračunavanja najvećeg zajedničkog delioca brojeva \(33\) i \(24\) imamo naredni niz jednakosti: \(\mathrm{nzd}(33, 24)=\mathrm{nzd}(24, 9)=\mathrm{nzd}(9, 6)=\mathrm{nzd}(6, 3)=\mathrm{nzd}(3, 0)=3\). Prateći unazad niz deljenja sa ostatkom dobijamo: \(d=3=9-6=9-(24-2\cdot 9)=3\cdot 9-24=3\cdot(33-24)-24=3\cdot 33-4\cdot 24\), odnosno \(x=3,y=-4\).
Prethodna induktivna konstrukcija pogodna je za rekurzivnu implementaciju jer nove vrednosti promenljivih \(x\) i \(y\) dobijamo na osnovu prethodnih. U narednoj implementaciji, vrednost koju funkcija vraća jeste najveći zajednički delilac datih brojeva, dok vrednosti koeficijenata \(x\) i \(y\) vraćamo preko referenci, kroz listu parametara funkcije.
Primetimo da je baza indukcije u implementaciji slučaj \(d = r_k = 1\cdot r_k + 0\cdot r_{k+1}\).
// funkcija koja vraca nzd brojeva a i b i racuna koeficijente x i y
int nzdProsireni(int a, int b, int &x, int &y) {
// ako je b jednako 0, onda je nzd(a, b) = a
if (b == 0) {
x = 1;
y = 0;
return a;
}
int x1, y1;
// rekurzivno resavamo problem za naredna dva elementa u nizu ostataka,
// a to su brojevi b i a%b
int nzd = nzdProsireni(b, a % b, x1, y1);
// azuriramo koeficijente
x = y1;
y = x1 - (a / b) * y1;
return nzd;
} Primetimo da se u ovoj verziji algoritama dva puta prolazi kroz količnike i ostatke. U prolazu unapred se određuje vrednost NZD, a zatim se u prolazu unazad određuju koeficijenti (u rekurzivnoj implementaciji taj drugi prolaz se izvršava tek nakon što se stigne do izlaza iz rekurzije). Zato se ovaj algoritam teže implementira nerekurzivno (i memorijska složenost mu je, kao i vremenska, \(\log(a+b)\), jer zahteva istovremeno čuvanje više stek okvira).
U prethodnom izvođenju smo sve vreme poslednji ostatak \(d=r_k\) predstavljali kao celobrojnu linearnu kombinaciju dva susedna elementa iz niza ostataka počev od \(r_{k-1}\) i \(r_{k-2}\). Alternativno, moguće je jednu po jednu vrednost iz niza ostataka počev od \(r_0\) predstaviti kao celobrojnu linearnu kombinaciju brojeva \(a\) i \(b\) i, na kraju, i broj \(r_k\) predstaviti na ovaj način. Naime, pošto je \(r_0 = a\) i \(r_1 = b\), važi: \[\begin{eqnarray*} r_0&=&1\cdot a+0\cdot b \\ r_1&=&0\cdot a+1\cdot b \end{eqnarray*}\]
odnosno za \(r_0=a\) važi \(x_0=1\) i \(y_0=0\), a za \(r_1=b\) važi \(x_1=0\) i \(y_1=1\).
Želimo da \(r_{i+1}\) predstavimo kao celobrojnu linearnu kombinaciju brojeva \(a\) i \(b\), ako znamo da važi: \[\begin{eqnarray*} r_{i-1}&=&x_{i-1}\cdot a+y_{i-1}\cdot b \\ r_{i}&=&x_{i}\cdot a+y_{i}\cdot b \end{eqnarray*}\]
Na osnovu jednakosti (1), tj. veze \(r_{i+1}=r_{i-1}-q_i\cdot r_i\) dobijamo:
\[r_{i+1}=(x_{i-1}\cdot a+y_{i-1}\cdot b)-q_i(x_{i}\cdot a+y_{i}\cdot b)=(x_{i-1}-q_ix_i)\cdot a+(y_{i-1}-q_iy_i)\cdot b\]
Dakle, vrednosti \(x_{i+1}\) i \(y_{i+1}\) možemo izračunati na osnovu prethodnih vrednosti \(x_{i-1}\) i \(x_i\), odnosno \(y_{i-1}\) i \(y_i\), tj. važi naredna veza: \[\begin{eqnarray*} x_{i+1}&=&x_{i-1}-q_ix_i\\ y_{i+1}&=&y_{i-1}-q_iy_i \end{eqnarray*}\]
Na osnovu ovih veza dolazi se do naredne C++ implementacije iterativnog algoritma za rešavanje polaznog problema.
// funkcija koja vraca nzd brojeva a i b i racuna koeficijente x i y
int nzdProsireni(int a, int b, int &x, int &y) {
// vrednost x i y za r_0 = a
int x_preth = 1;
int y_preth = 0;
// vrednost x i y za r_1 = b
int x_tek = 0;
int y_tek = 1;
while (b != 0) {
// azuriramo vrednosti za a i b
// kao u standardnom Euklidovom algoritmu
int q = a/b;
int r = a - q * b;
a = b;
b = r;
// azuriramo tekucu i prethodnu vrednost niza x
int xpom = x_preth - q * x_tek;
x_preth = x_tek;
x_tek = xpom;
// azuriramo tekucu i prethodnu vrednost niza y
int ypom = y_preth - q * y_tek;
y_preth = y_tek;
y_tek = ypom;
}
// postavljamo konacne vrednosti za x i y
// kao vrednosti x i y za r_k
x = x_preth;
y = y_preth;
// vracamo a kao nzd brojeva
return a;
} Primer 3.1.5. Primenimo algoritam na brojeve \(33\) i \(24\).
\[ \begin{array}{cccccccccccrc} 33& & & & & & & & &=& 1\cdot 33&+&0\cdot 24\\ 24& & & & & & & & &=& 0\cdot 33&+&1\cdot 24\\ 9 &=&33 &-& 1\cdot 24 &=&(1\cdot 33+0\cdot 24)&-&1\cdot(0\cdot 33+1\cdot 24) &=& 1\cdot 33&-&1\cdot 24\\ 6 &=&24 &-& 2\cdot 9 &=&(0\cdot 33+1\cdot 24)&-&2\cdot(1\cdot 33-1\cdot 24) &=& -2\cdot 33&+&3\cdot 24\\ 3 &=&9 &-& 1\cdot 6 &=&(1\cdot 33-1\cdot 24)&-&1\cdot(-2\cdot 33+3\cdot 24) &=& 3\cdot 33&-&4\cdot 24\\ 0 &=&6 &-& 2\cdot3 \end{array} \]
Veze između \((x_{i+1}, y_{i+1})\) i \((x_i, y_i)\) su bile izažene na način pogodan implementaciji (naredni koeficijenti su bili izraženi preko prethodniih). Primetimo da se ove veze mogu izraziti i na sledeći način, tako da je oblik veza isti i za količnike i ostatke \(r\) i za koeficijente \(x\) i \(y\):
\[ \begin{array}{ccccc} r_{i-1} &=& q_ir_i &+& r_{i+1}\\ x_{i-1} &=& q_ix_i &+& x_{i+1}\\ y_{i-1} &=& q_iy_i &+& y_{i+1} \end{array} \]
Pri tom u svakoj koloni u prethodnim jednakostima važi veza istog oblika:
\[ \begin{array}{ccrcr} r_{i-1} &=& x_{i-1}a &+& y_{i-1}b\\ r_{i} &=& x_{i}a &+& y_{i}b\\ r_{i+1} &=& x_{i+1}a &+& y_{i+1}b\\ \end{array} \]
U narednom apletu možete proveriti svoje razumevanje rada proširenog Euklidovog algoritma.
Broj operacija koje se izvršavaju u proširenom Euklidovom algoritmu proporcionalan je broju operacija u standardnom Euklidovom algoritmu, tj. iznosi \(O(\log(a+b))\), pa je i ovo izrazito efikasan algoritam. Primetimo i da se u ovoj varijanti algoritma vrši samo jedan prolaz, pa se nakon određivanja narednih vrednosti koeficijenata, prethodne mogu zaboraviti. Memorijska složenost je, stoga, konstantna (za razliku od prethodne, rekurzivne varijante koja zbog čuvanja stek okvira zahteva prostor \(O(\log(a+b))\)).
Iz prethodno opisanih razloga ova (jednoprolazna) varijanta algoritma je poželjnija od prethodne (dvoprolazne), pa stoga neki autori pod nazivom prošireni Euklidov algoritam podrazumevaju samo ovu varijantu.
Jedna od primena Bezuovog stava i proširenog Euklidovog algoritma je u rešavanju jedne klase Diofantovih jednačina, tzv. linearnih Diofantovih jednačina koje su oblika \(a\cdot x+b\cdot y=c\).
Problem. Za date nenegativne cele brojeve \(a\) i \(b\) (koji nisu istovremeno jednaki nuli) i nenegativan ceo broj \(c\) odrediti cele brojeve \(x\) i \(y\) tako da važi \(a\cdot x + b\cdot y = c\).
Naredni aplet prikazuje vrednost linearne kombinacije \(a\cdot x+b\cdot y\) za različite vrednosti koeficijenata \(x\) i \(y\). Pokušajte samostalno da otkrijete potreban i dovoljan uslov da bi se neka vrednost \(c\) mogla izraziti kao ta linearna kombinacija.
Bezuov stav daje jedno rešenje jednačine \(ax + by = d\), za \(d=\mathrm{nzd}(a, b)\). Naredni stav govori o strukturi svih rešenja.
Lema 3.1.1. [Sva rešenja Bezuovog identiteta] Ako je \((x_0, y_0)\) jedno rešenje jednačine \(ax + by = d\), gde je \(d = \mathrm{nzd}(a, b)\), onda su sva rešenja oblika \(x = x_0 - k\frac{b}{d}\), \(y = y_0 + k\frac{a}{d}\), za \(k \in \mathbb{Z}\). Postoje tačno dva “mala” para rešenja, za koje je \(|x| \leq |b/d|\) i \(|y|\leq |a/d|\). Jednakost važi ako i samo ako je jedan od brojeva \(a\) ili \(b\) umnožak onog drugog.
Dokaz. Pošto je \(ax_0 + by_0 = d = ax+by\), važi \(a(x_0 - x) = b(y - y_0)\). Ova se veza može podeliti sa \(d\) i i dobija se \(\frac{a}{d}(x_0 - x) = \frac{b}{d}(y - y_0)\). Brojevi \(\frac{a}{d}\) i \(\frac{b}{d}\) su uzajamno prosti pa mora da postoji ceo broj \(k\) takav da je \(x_0 - x = k\frac{b}{d}\), a \(y - y_0 = k\frac{a}{d}\). Odatle se dobija i opšte rešenje:
\[(x, y) = \Bigl( x_0 - k\frac{b}{d}, y_0 + k\frac{a}{d} \Bigr)\]
“Mali” parovi rešenja se dobijaju tako što se za \(k\) uzme bilo koji od dva cela broja koji su najbliži vrednosti \(x_0 \frac{d}{b}\). \(\Box\)
Napomenimo da prošireni Euklidov algoritam uvek vraća jedan od dva “mala” para rešenja o kojima se govori u prethodnoj lemi.
Primer 3.1.6. Razmotrimo sada jednačinu \(4x+10y=2\). Važi \(d = \mathrm{nzd}(4, 10) = 2\), pa korišćenjem proširenog Euklidovog algoritma najveći zajednički delilac \(d=2\) brojeva \(a=4\) i \(b=10\) izražavamo kao njihovu celobrojnu linearnu kombinaciju: \(x_0a + y_0b = d\), tj. \(-2\cdot 4+1\cdot 10=2\). Ostala rešenja jednačine su oblika \(x = x_0 - k\cdot b/d = -2 - 5k\) i \(y = y_0 + k\cdot a/d = 1 + 2k\). Zaista, važi \(4x + 10y = 4(-2-5k) + 10(1+2k) = (-8 + 10) + (20k - 20k) = 2\). “Mala” rešenja su ona za koja važi \(|x| \leq |b/d| = 5\) i \(|y| \leq |a/d| = 2\) i to su jedino \((-2, 1)\) i \((3, -1)\).
Teorema 3.1.4. [Postojanje rešenja linearne diofantske jednačine] Da bi jednačina \(a\cdot x+b\cdot y=c\) imala bar jedno rešenje, potrebno je i dovoljno da \(d=\mathrm{nzd}(a, b)\) deli \(c\).
Dokaz. Naime, pošto \(d\) deli levu stranu jednačine, mora da deli i desnu, pa je ovaj uslov potreban. Dokažimo da je i dovoljan, tako što ćemo opisati postupak konstrukcije rešenja. Naime, ako je ovaj uslov ispunjen, jedno od rešenja ove jednačine lako se dobija narednim postupkom: najpre se \(d\) izrazi u obliku \(d=x'\cdot a+y'\cdot b\) a zatim se množenjem leve i desne strane jednakosti celim brojem \(c/d\) dobija:
\[c=\frac{x'c}{d}\cdot a +\frac{y'c}{d}\cdot b\]
tj. jedno rešenje polazne jednačine predstavlja par
\[(x_0,y_0)=\Bigl(\frac{x'c}{d},\frac{y'c}{d}\Bigr)\]
Struktura svih rešenja sledi iz leme 3.1.1, tj. sva rešenja su opisana parom:
\[(x, y) = \Bigl(\frac{x'c -kb}{d}, \frac{y'c +ka}{d}\Bigr)\]
\(\Box\)
Primer 3.1.7. Razmotrimo jednačinu \(4x+10y=7\). Važi da je \(\mathrm{nzd}(4, 2) = 2\), međutim \(2\) ne deli desnu stranu jednakosti, tj. broj \(7\), te ova Diofantova jednačina nema rešenja.
Primer 3.1.8. Razmotrimo sada jednačinu \(4x+10y=8\). Dakle, \(a=4\), \(b=10\) i \(c=8\). Važi \(d = \mathrm{nzd}(4, 10) = 2\) i \(2 \,\vert\, 8\), pa pošto \(d\,\vert\,c\), ova jednačina ima rešenja. Jedno njeno rešenje možemo dobiti na sledeći način: korišćenjem proširenog Euklidovog algoritma najveći zajednički delilac brojeva \(a=4\) i \(b=10\) izražavamo kao njihovu celobrojnu linearnu kombinaciju: \(x'a + y'b = d\), tj. \(-2\cdot 4+1\cdot 10=2\), a zatim obe strane jednakosti množimo brojem \(c/d = 8/2 = 4\) čime dobijamo: \(x_0a+y_0b=c\), tj. \(-8\cdot 4+4\cdot 10=8\). Dakle, jedno rešenje ove jednačine je \(x_0=-8\) i \(y_0=4\). Ostala rešenja su oblika \(x = x_0 - k\cdot b/d = -8 - 5k\) i \(y = y_0 + k\cdot a/d = 4 + 2k\). Zaista, važi \(4x + 10y = 4(-8-5k) + 10(4+2k) = (-32 + 40) + (20k - 20k) = 8\).
Dalje primene proširenog Euklidovog algoritma biće prikazane u narednim poglavljima (u poglavlju 3.4 ovaj algoritam se primenjuje na problem određivanja modularnog multiplikativnog inverza, a u poglavlju 3.6 na rešavanje sistema kongruencija primenom Kineske teoreme o ostacima).
Zadaci: