Svaka od \(k^n\) nizova treba da se javi tačno jednom kao segmenta traženog niza, pri čemu se svaka dva uzastopna segmenta poklapaju na \(n-1\) pozicija. Dva segmenta mogu biti uzastpna ako i samo ako se poslednjih \(n-1\) brojeva prvog poklapa sa \(n-1\) prvih brojeva drugog segmenta. Ovo je moguće modelovati usmerenim grafom. Svaki niz brojeva iz intervala \([0, k)\) dužine \(n\) možemo predstaviti jednim čvorom grafa (graf, dakle, ima \(n^k\) čvorova), a grana od čvora \(A\) do čvora \(B\) postoji ako i samo ako niz \(A\) i niz \(B\) mogu da budu uzastopni segmenti (koji se preklapaju na \(n-1\) pozicija). Primeri takvih grafova za \(k=2\) i \(n=1\), \(n=2\) i \(n=3\), su prikazani na slici.
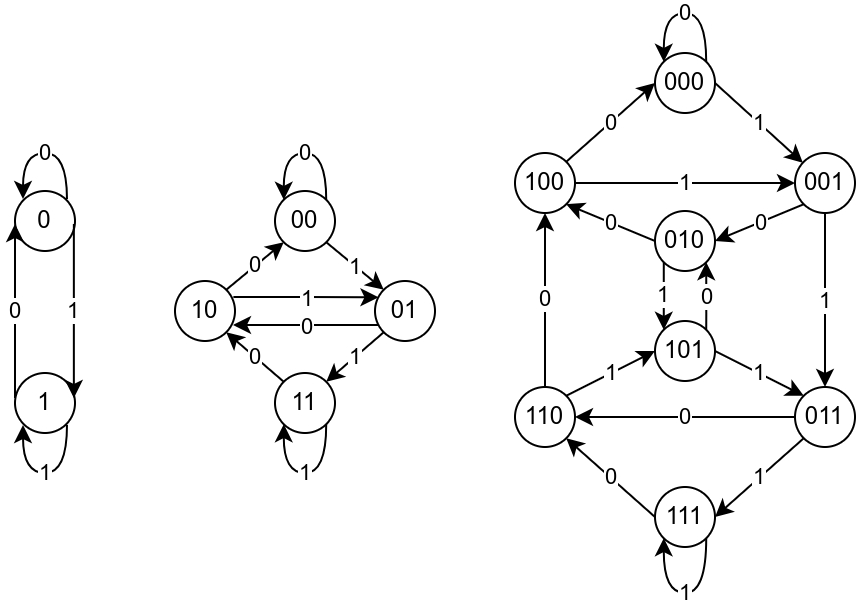
Svaki put u grafu odgovara binarnom nizu i obratno. Na primer, de Brujnom nizu 00111010 za \(n=3\) i \(k=2\), odgovara put kroz čvorove 001, 011, 111, 110, 101, 010.
DeBrujnov niz se može dobiti pronalaskom Hamiltonovog ciklusa u grafu (jer Hamiltonov ciklus obilazi svaki čvor tačno jednom, pre nego što se vrati u početni čvor). Dužina niza koja odgovara Hamiltonovom ciklusu je \(k^n + n - 1\), pri čemu se poslednjih \(n-1\) elemenata niza poklapa sa prvih \(n-1\) elemenata, pa se oni mogu izostaviti (što odgovara izostavljanju poslednjih \(n-1\) elemenata Hamiltonovog ciklusa.
Međutim, de Brujinov niz za dato \(n\) i \(k\) se može dobiti i od grafa za to \(k\) i \(n-1\). Svakom segmentu \(a_1, a_2, \ldots, a_{n-1}, a_n\) odgovara grana od čvora \(a_1, \ldots, a_{n-1}\) do čvora \(a_2, \ldots a_n\). U tom slučaju se kroz svaku granu prolazi samo jednom, što znači da de Brujnovim nizovima odgovaraju Ojlerovi ciklusi i obratno.
Zadatak ze zato može rešiti pronalaženjem Ojlerovog ciklusa u grafu za dato \(k\) i \(n-1\). Ojlerov ciklus možemo pronaći Hirholcerovim algoritmom. Ako znamo sve čvorove Ojlerovog ciklusa (pri čemu su prvi i poslednji jednaki), niz možemo dobiti čitajući redom njihove poslednje brojeve, i izostavljajući poslednji čvor.
U narednoj implementaciji rekurzivno nabrajamo sve varijacije i tako gradimo sve čvorove grafa kao eksplicitne niske cifara (implementacija bi se mogla unaprediti korišćenjem neke efikasnije reprezentacije grafa).
// pomocna funkcija za generisanje varijacija
void sviCvorovi(int m, int k, string& s, vector<string>& rezultat) {
if (m == 0) {
rezultat.push_back(s);
return;
}
for (int i = 0; i < k; i++) {
s[m-1] = '0' + i;
sviCvorovi(m-1, k, s, rezultat);
}
}
// cvorovi grafa su sve varijacije duzine m od azbuke {0, 1, .., k-1}
vector<string> sviCvorovi(int m, int k) {
vector<string> rezultat;
string s(m, ' ');
sviCvorovi(m, k, s, rezultat);
return rezultat;
}
int main() {
int n;
cin >> n;
int k;
cin >> k;
// generisemo vektor svih cvorova grafa
// cvorovi su varijacije duzine m od azbuke {0, 1, .., k-1}
vector<string> cvorovi = sviCvorovi(n-1, k);
// za svaki cvor pamtimo koja grana je na redu za obilazak
unordered_map<string, int> tekucaGrana;
// na pocetku nismo obisli nijednu granu
for (const string& cvor : cvorovi)
tekucaGrana[cvor] = 0;
// Ojlerov put određen čvorovima kroz koje se prolazi
vector<string> ojlerovPut;
stack<string> tekuciPut;
// krecemo, na primer, od cvora 00..00
tekuciPut.push(string(n-1, '0'));
while (!tekuciPut.empty()) {
string tekuciCvor = tekuciPut.top();
// ako postoji neobrađena grana iz tekućeg čvora
if (tekucaGrana[tekuciCvor] < k) {
// oznaka na toj grani
char grana = '0' + tekucaGrana[tekuciCvor]++;
// čvor do koga vodi ta grana
string sledeciCvor = tekuciCvor.substr(1) + string(1, grana);
tekuciPut.push(sledeciCvor);
} else {
ojlerovPut.push_back(tekuciCvor);
tekuciPut.pop();
}
}
// ispisujemo rezultujuci niz
// (dobijen od poslednjih brojki na cvorovima kojima prolazi Ojlerov put)
for (int i = 0; i < ojlerovPut.size() - 1; i++)
cout << ojlerovPut[i].back();
cout << endl;
return 0;
}#include <iostream>
#include <string>
#include <vector>
#include <unordered_map>
#include <stack>
using namespace std;
// pomocna funkcija za generisanje varijacija
void sviCvorovi(int m, int k, string& s, vector<string>& rezultat) {
if (m == 0) {
rezultat.push_back(s);
return;
}
for (int i = 0; i < k; i++) {
s[m-1] = '0' + i;
sviCvorovi(m-1, k, s, rezultat);
}
}
// cvorovi grafa su sve varijacije duzine m od azbuke {0, 1, .., k-1}
vector<string> sviCvorovi(int m, int k) {
vector<string> rezultat;
string s(m, ' ');
sviCvorovi(m, k, s, rezultat);
return rezultat;
}
int main() {
int n;
cin >> n;
int k;
cin >> k;
// generisemo vektor svih cvorova grafa
// cvorovi su varijacije duzine m od azbuke {0, 1, .., k-1}
vector<string> cvorovi = sviCvorovi(n-1, k);
// za svaki cvor pamtimo koja grana je na redu za obilazak
unordered_map<string, int> tekucaGrana;
// na pocetku nismo obisli nijednu granu
for (const string& cvor : cvorovi)
tekucaGrana[cvor] = 0;
// Ojlerov put određen čvorovima kroz koje se prolazi
vector<string> ojlerovPut;
stack<string> tekuciPut;
// krecemo, na primer, od cvora 00..00
tekuciPut.push(string(n-1, '0'));
while (!tekuciPut.empty()) {
string tekuciCvor = tekuciPut.top();
// ako postoji neobrađena grana iz tekućeg čvora
if (tekucaGrana[tekuciCvor] < k) {
// oznaka na toj grani
char grana = '0' + tekucaGrana[tekuciCvor]++;
// čvor do koga vodi ta grana
string sledeciCvor = tekuciCvor.substr(1) + string(1, grana);
tekuciPut.push(sledeciCvor);
} else {
ojlerovPut.push_back(tekuciCvor);
tekuciPut.pop();
}
}
// ispisujemo rezultujuci niz
// (dobijen od poslednjih brojki na cvorovima kojima prolazi Ojlerov put)
for (int i = 0; i < ojlerovPut.size() - 1; i++)
cout << ojlerovPut[i].back();
cout << endl;
return 0;
}