Ако са \(a\), \(b\) и \(c\) обележимо број сваке од три врсте инсеката, а са \(t\) величину сваког тима, бројеви \(a\), \(b\) и \(c\) морају бити дељиви са \(t\) (јер сваки инсект мора бити укључен тачно у један тим). Дакле, тражимо највећи број \(t\) који дели бројеве \(a\), \(b\) и \(c\), а то је њихов највећи заједнички делилац (НЗД).
НЗД три броја се може одредити као НЗД од НЗД-а прва два и трећег броја, тј. важи \(nzd(a, b, c) = nzd(nzd(a, b), c)\). Довољно је, дакле, да опишемо поступак одређивања НЗД два броја.
Еуклидов алгоритам
За одређивање НЗД најбоље је употребити чувени Еуклидов алгоритам. Оригинална формулација Еуклидовог алгоритма заснована је на одузимању.
Ако су два броја једнака тј. ако је \(a=b\), тада им је и њихов НЗД једнак.
У супротном се проблем може свести на проналажење НЗД мањег од два броја и разлике два броја. На пример, ако је \(a > b\), тада је \(nzd(a, b) = nzd(a-b, b)\).
Алгоритам се може илустровати и геометријски (и у директној је вези са проблемом одређивања максималне димензије квадрата којима може да се поплоча правоугаоно поље димензија \(a \times b\)).
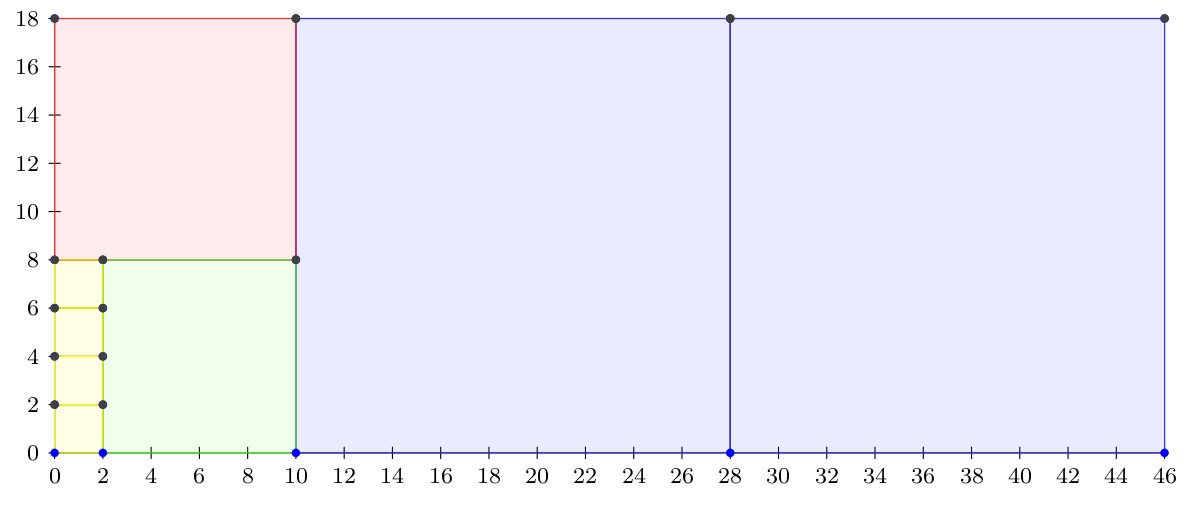
Пример. Претпоставимо да је дат правоугаоник чије су дужине страница \(a\) и \(b\) и да је потребно одредити највећу дужину странице квадрата таква да се правоугаоник може поплочати квадратима те димензије. Ако је полазни правоугаоник димензије \(a = 46\) и \(b = 18\), тада се прво из њега могу исећи два квадрата димензије \(18\) пута \(18\) и остаће нам правоугаоник димензије \(18\) пута \(10\). Јасно је да ако неким мањим квадратима успемо да поплочамо тај преостали правоугаоник, да ћемо тим квадратима успети да поплочамо и ове квадрате димензије \(18\) пута \(18\) (јер ће димензија тих малих квадрата делити број \(18\)), па ћемо самим тим моћи поплочати и цео полазни правоугаоник димензија \(46\) пута \(18\). Од правоугаоника димензије \(18\) пута \(10\) можемо исећи квадрат димензије \(10\) пута \(10\) и преостаће нам правоугаоник димензије \(10\) пута \(8\). Поново, квадратићи којима ће се моћи поплочати тај преостали правоугаоник ће бити такви да се њима може поплочати и исечени квадрат димензије \(10\) пута \(10\). Од тог правоугаоника исецамо квадрат \(8\) пута \(8\) и добијамо правоугаоник димензије \(8\) пута \(2\). Њега можемо разложити на четири квадрата димензије \(2\) пута \(2\) и то је највећа димензија квадрата којим се може поплочати полазни правоугаоник.
Имплементација може бити рекурзивна, која директно прати претходну дефиницију. Могуће је једноставно направити и итеративну имплементацију, у којој се у сваком кораку вредност већег од два броја мења њиховом разликом.
#include <iostream>
using namespace std;
// izracunavanje najveceg zajednickog delioca brojeva a i b
int nzd(int a, int b) {
// Euklidov algoritam sa oduzimanjem
while (a != b) {
if (a > b)
a -= b;
else
b -= a;
}
return a;
}
// izracunavanje najveceg zajednickog delioca brojeva a, b i c
int nzd(int a, int b, int c) {
return nzd(nzd(a, b), c);
}
int main() {
// ucitavamo 3 broja
int a, b, c;
cin >> a >> b >> c;
// izracunavamo njihov nzd
cout << nzd(nzd(a, b), c) << endl;
return 0;
}Доказ коректности. Ако неки број \(d\) дели бројеве \(a\) и \(b\), тада он дели и њихову разлику. Дакле, \(d=nzd(a, b)\) сигурно дели и \(b\) и \(a-b\). Ако он не би био НЗД бројева \(a-b\) и \(b\), тада би постојао неки већи број \(d'\) који би делио и \(a-b\) и \(b\). Међутим, тада би \(d'\) делио и збир \(a = (a-b) + b\), па би био делилац бројева \(a\) и \(b\), који је већи од \(d\), што је контрадикција са тим да је \(d\) НЗД бројева \(a\) и \(b\).
Ако је \(a < b\), тада се веома слично може доказати да је \(nzd(a, b) = nzd(a, b-a)\).
Сложеност. Најгори случај наступа када је разлика између два броја јако велика (ако је \(a=1\), он ће се одузимати од \(b\) све док он не постане 1, за шта је потребно \(b-1\) корака). Може се показати да је сложеност линеарна у односу на већи од два броја, што се може записати као \(O(\max{(a, b)})\) или \(O(a+b)\). Ако се сложеност рачуна у односу на број цифара броја (што је величина улаза), онда је она заправо експоненцијална.
Поправљање сложености коришћењем дељења
Пример. Размотримо одређивање НЗД на једном примеру.
\(nzd(279, 45)\) = \(nzd(234, 45)\) = \(nzd(189, 45)\) = \(nzd(144, 45)\) = \(nzd(99, 45)\) = \(nzd(54, 45)\) = \(nzd(9, 45)\) = \(nzd(9, 36)\) = \(nzd(9, 27)\) = \(nzd(9, 18)\) = \(nzd(9, 9)\) = \(9\).
Можемо приметити дугачак низ корака у којима се мало по мало од броја \(279\) одузима број \(45\), све док се не дође до броја који је мањи од броја \(45\). За тим нема потребе, јер знамо да ће се после тог дугог низа поступак зауставити када нам један аргумент буде баш \(45\), а други буде једнак остатку при дељењу броја \(279\) бројем \(45\), а то је број \(9\). Дакле, уместо да итеративно, тај остатак рачунамо узастопним одузимања, бољи приступ је да применимо дељење и у једном кораку га израчунамо као остатак при дељењу. Ако сличан принцип применимо на бројеве \(9\) и \(45\), доћи ћемо до тога да ће нам остати број \(9\) и остатак при дељењу та два броја, што је нула. То није баш у потпуности једнако као у случају одузимања, где смо се зауставили код пара \((9, 9)\), међутим, сасвим је исправно и може се сматрати продужењем претходног поступка у ком би се пре пријављивања резултата урадило још једно одузимање и дошло се до тога да је један од бројева једнак нули, када је НЗД једнак другом броју.
Бржи Еуклидов алгоритам, у ком се користи дељење, заснован је на следећим тврђењима.
НЗД било ког броја \(a\) и нуле је тај број \(a\) (он дели и нулу и самог себе и највећи је такав број јер није могуће да неки број већи од \(a\) дели број \(a\)).
НЗД бројева \(a\) и \(b\), када \(b\) није нула, једнак је НЗД броја \(b\) и остатка при дељењу \(a\) бројем \(b\), тј. \(nzd(a, b) = nzd(b, a \,\mathrm{mod}\,b)\).
Приметимо да нема потребе анализирати који је број мањи, а који је већи. Ако је \(a < b\), тада ће важити \(a \,\mathrm{mod}\,b = a\), па ће се у првом кораку добити да је \(nzd(a, b) = nzd(b, a)\). Пошто је \(a \,\mathrm{mod}\,b < b\), једном када је први аргумент већи од другог, то ће тако остати до краја.
Еуклидов алгоритам, дакле, допушта веома једноставну рекурзивну карактеризацију.
Имплементацију Еуклидовог алгоритма можемо извршити итеративно, тако што у петљи која се извршава све док је број \(b\) већи од нуле пар променљивих \((a, b)\) мењамо вредностима \((b, a \,\mathrm{mod}\,b)\). Наивни покушај да се то уради на следећи начин:
a = b;
b = a % b;није коректан, јер се приликом израчунавања остатка користи промењена вредност променљиве a. Зато је неопходно употребити помоћну променљиву. На пример:
tmp = b;
b = a % b;
a = tmp;На крају петље вредност \(b\) једнака је нули, тако да као резултат можемо пријавити текућу вредност броја \(a\).
#include <iostream>
using namespace std;
// izracunavanje najveceg zajednickog delioca brojeva a i b
int nzd(int a, int b) {
// Euklidov algoritam
while (b > 0) { // dok b ne postane nula
int tmp = b; // par (a, b) menjamo parom (b, a % b)
b = a % b; // jer je nzd(a, b) = nzd(b, a % b)
a = tmp;
}
return a; // nzd(a, 0) = a
}
// izracunavanje najveceg zajednickog delioca brojeva a, b i c
int nzd(int a, int b, int c) {
return nzd(nzd(a, b), c);
}
int main() {
// ucitavamo 3 broja
int a, b, c;
cin >> a >> b >> c;
// izracunavamo njihov nzd
cout << nzd(a, b, c) << endl;
return 0;
}Доказ коректности. Докажимо формално коректност алгоритма. На основу дефиниције целобројног дељења важи да је \(a = (a\,\mathrm{div}\,b)\cdot b + (a \,\mathrm{mod}\,b)\). Обележимо са \(d\) НЗД бројева \(b\) и \(a\,\mathrm{mod}\,b\). Да бисмо доказали да је он уједно НЗД бројева \(a\) и \(b\) довољно је доказати да он дели та два броја и да сваки број који дели та два броја дели њега.
Пошто број \(d\) дели бројеве \(b\) и \(a \,\mathrm{mod}\,b\), он дели оба сабирка на десној страни, па зато дели и њихов збир који је једнак \(a\) и зато дели и \(a\) и \(b\).
Даље, ако неки број \(d'\) дели бројеве \(a\) и \(b\) он мора делити и број \(a\,\mathrm{mod}\,b\) (јер се он може исказати као разлика два броја дељивих бројем \(d'\)), па пошто је \(d'\) делилац бројева \(b\) и \(a\,\mathrm{mod}\,b\), он мора делити и њихов НЗД тј. мора делити број \(d\).
Еуклидов алгоритам који је заснован на дељењу можемо представити и на следећи начин:
\[ \begin{array}{rcll} r_0 &=& a\\ r_1 &=& b\\ r_2 &=& r_0 - q_1r_1, &\quad 0 < r_2 < r_1\\ \ldots\\ r_{i+1} &=& r_{i-1} - q_ir_i, & \quad 0 < r_{i+1} < r_i\\ \ldots \\ r_{k} &=& r_{k-2} - q_{k-1}r_{k-1}, &\quad 0 < r_k < r_{k-1}\\ r_{k+1} &=& r_{k-1} - q_kr_k, & \quad 0 = r_{k+1} \end{array} \]
Вредност \(r_k\) је НЗД бројева \(a\) и \(b\). Заиста, пошто је \(r_{k+1}=0\), важи да је \(r_{k-1} = q_kr_k\), па број \(r_k\) дели \(r_{k-1}\). Међутим, пошто је \(r_{k-2} = q_{k-1}r_{k-1} + r_{k}\), он дели и \(r_{k-2}\). Сличним резоновањем, уназад, може се закључити да \(r_k\) дели и \(r_1\) и \(r_0\) тј. \(a\) и \(b\). Обратно, ако неки број дели и \(a\) и \(b\) онда он дели и \(r_0\) и \(r_1\), а пошто је \(r_2 = r_0 - q_1r_1\), он дели и \(r_2\). Сличним резоновањем, унапред, може се закључити да тај број мора делити и \(r_k\). Стога је \(r_k\) НЗД бројева \(a\) и \(b\).
У сваком кораку алгоритма одржавамо две узастопне вредности низа \(r_i\). У почетку, то су чланови \(r_0\) и \(r_1\) тј. оригиналне вредности \(a\) и \(b\). Важи да је \(q_1 = a\,\mathrm{div}\,b\), а \(r_2 = a \,\mathrm{mod}\,b\). У другом кораку променљиве \(a\) и \(b\) треба да имају вредности чланова \(r_1\) и \(r_2\), што значи да се пар променљивих \(a\), \(b\) мења вредностима \(b\) и \(a\,\mathrm{mod}\,b\), што је управо оно што смо радили у претходно описаном коду. Поступак се наставља све док пар узастопних вредности не постане \(r_k\), \(r_{k+1}\), тј., пошто пар узастопних вредности одржавамо у променљивама \(a\) и \(b\), док \(b\) не постане нула и тада је НЗД који је једнак \(r_k\) садржан у променљивој \(a\).
Сложеност. Приметимо да се после највише једног корака осигурава да је \(a > b\) (јер се у сваком кораку пар \((a, b)\) мења паром \((b, a \,\mathrm{mod}\,b)\), а увек важи да је \(a \,\mathrm{mod}\,b < b\)). После било које две итерације се од пара \((a, b)\) долази до пара \((a \,\mathrm{mod}\,b, b \,\mathrm{mod}\,(a \,\mathrm{mod}\,b))\) (наравно, под претпоставком да је \(b \neq 0\) и да је \(a \,\mathrm{mod}\,b \neq 0\)). Докажимо да је \(a \,\mathrm{mod}\,b < a/2\). Ако је \(b \leq a/2\), тада је \(a \,\mathrm{mod}\,b < b \leq a/2\). У супротном, за \(b > a/2\) важи да је \(a \,\mathrm{mod}\,b = a - b < a/2\). Зато се први аргумент после свака два корака смањи бар двоструко. До вредности 1 први аргумент стигне у логаритамском броју корака у односу на већи од полазна два броја и тада други број сигурно достиже нулу (јер је строго мањи од првог) и поступак се завршава. Дакле, сложеност је логаритамска у односу на већи од два броја, што може да се запише и као \(O(\log(a + b))\). Ако се сложеност рачуна у односу на број цифара броја (што је величина улаза), онда је она заправо линеарна.