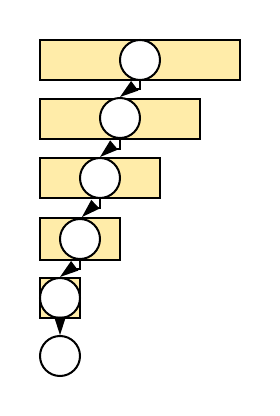
Сложеност рекурзивних функција се често може описати рекурентним једначинама. Решење рекурентне једначине је функција \(T(n)\) и за решење ћемо рећи да је у затвореном облику ако је изражено као елементарна функција по \(n\) (и не укључује са десне стране поновно реферисање на функцију \(T\)). Често ћемо се задовољити да уместо потпуно прецизног решења знамо само његово асимптотско понашање. Подсетимо се неколико најчешћих рекурентних једначина.
У првој групи се проблем своди на проблем димензије која је тачно за један мања од димензије полазног проблема.
У другој групи се проблем своди на два (или више) проблема чија је димензија за један или два мања од димензије полазног проблема. То обично доводи до експоненцијалне сложености.
У наредној групи се проблем своди на један (или више) потпроблема који су значајно мање димензије од полазног (обично су бар дупло мањи). Ово доводи до полиномијалне сложености, па често и до веома ефикасних решења.
Ако су границе у самим једначинама егзактне, скоро у свим претходно набројаним једначинама дато решење није само горње ограничење, већ је асимптотски егзактно. На пример, решење једначине \(T(n) = 2T(n/2) + \Theta(n)\), \(T(1) = \Theta(1)\) има решење \(T(n) = \Theta(n\log{n})\). Изузетак је пример Фибоначијевог низа где понашање јесте експоненцијално, али основа није \(2\), већ златни пресек \((1 + \sqrt{5}) / 2\).
Потпуно формално и прецизно извођење и доказивање асимптотског понашања решења ових једначина нам неће бити у директном фокусу. Много важније је стећи неку интуицију зашто су решења баш таква каква јесу (уз одређену дозу резерве, јер овакве грубе апроксимације некада могу довести до грешке). Један начин да се то уради је да се крене са “одмотавањем” рекурзије и да се види до чега се долази.
На пример, код једначине \(T(n) = T(n-1) + O(1)\) и \(T(0) = O(1)\), након одмотавања добијамо да важи \[\begin{eqnarray*} T(n) &=& T(n-1) + O(1)\\ &=& T(n-2) + O(1) + O(1)\\ &=& T(n-3) + O(1) + O(1) + O(1)\\ &=& \ldots \\ &=& T(0) + n \cdot O(1) \\ &=& O(1) + n \cdot O(1)\\ &=& O(n). \end{eqnarray*}\]

Наравно, у оваквим неформалним извођењима треба бити обазрив. Иако је \(O(1) + O(1) = O(1)\), када имамо \(n\) сабирака њихов збир више није \(O(1)\) него \(O(n)\). Мало прецизнији можемо бити ако уместо \(O(1)\) употребимо неку константу \(c\) (која сигурно постоји) и одмотамо једначину \(T(n) = T(n-1) + c\), \(Т(0) = d\).
Код једначине \(T(n) = T(n-1) + O(n)\), \(T(0) = O(1)\) слично добијамо \(n\) сабирака који су сви \(O(n)\) тако да је укупна сума \(O(n^2)\). Поставља се питање да ли је ова граница егзактна тј. да ли је могуће да је сложеност мања од изведеног горњег ограничења. Претпоставимо да је \(T(n) = T(n-1) + cn\) и да је \(T(0) = d\) (наравно, \(О(n)\) може бити и нека друга линеарна, па и нелинеарна функција, али избором константе \(c\) можемо постићи да је она одозго ограничена изразом \(cn\)). Тада је
\[\begin{eqnarray*} T(n) &=& T(n-1) + cn \\ &=& T(n-2) + ц(n-1) + cn \\ &=& \ldots\\ &=& T(0) + c(1 + \ldots + n)\\ &=& O(1) + cn(n+1)/2, \end{eqnarray*}\]
тако да је \(T(n) = \Theta(n^2)\).
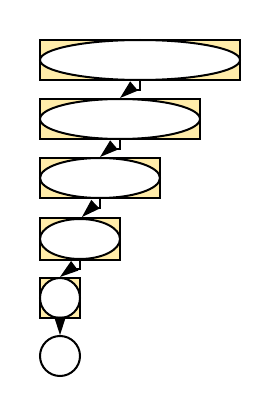
Покажимо још и шта се дешава са једначином \(T(n) = T(n-1) + c\log{n}\), \(T(0) = O(1)\). Одмотавањем добијамо
\[\begin{eqnarray*} T(n) &=& T(n-1) + c\log{n}\\ &=& T(n-2) + c\log{(n-1)} + c\log(n)\\ &=& \ldots \\ &=& O(1) + c(\log{1} + \ldots + \log{n}). \end{eqnarray*}\]
Пошто је логаритам растућа функција, сваки од \(n\) чланова овог збира ограничен је одозго вредношћу \(\log{n}\). Зато је збир \(O(n \log{n})\). Докажимо да ово ограничење није превише грубо. Важи да је
\[\log{1} + \log{2} + \ldots + \log{n} \geq \log{(n/2)} + \log{(n/2 + 1)} + \ldots + \log{n},\]
јер је првих \(n/2\) чланова који су из суме изостављени сигурно ненегативно. Пошто је логаритам растућа функција (за основу већу од \(1\)), сви сабирци у овом збиру су већи или једнаки \(\log{(n/2)}\), па је
\[\log{(n/2)} + \log{(n/2 + 1)} + \ldots + \log{n} \geq \log{(n/2)} + \log{(n/2)} + \ldots + \log{(n/2)}.\]
Збир на десној страни има \(n/2\) истих сабирака и једнак је \((n/2)\cdot \log{(n/2)}\). Стога је почетни збир логаритама ограничен и одоздо и одозго функцијама које су \(\Theta({n\log{n}})\), па је и сам \(\Theta({n\log{n}})\).
Још један начин да се ово покаже који се често среће у литератури је следећи. Збир логаритама, једнак је логаритму производа, па заправо овде рачунамо вредност \(\log{1\cdot\ldots\cdot n} = \log{n!}\). По Стирлинговој формули \(n!\) се понаша као \(\sqrt{2\pi n}\left(\frac{n}{e}\right)^n\). Зато се \(\log{n!}\) понаша као \(n\log n - n + O(\log{n})\), па је укупан збир \(\Theta(n\log{n})\).
Можемо уочити неке правилности. Код свих једначина облика \(T(n) = T(n-1) + f(n)\), \(T(0) = c\), након одмотавања добијамо да је \(T(n) = c + f(1) + f(2) + \ldots + f(n)\), тако да се одређивање асимптотског понашања своди на сумирање.
Збир \(n\) сабирака реда \(1+2+\ldots+n\) има вредност \(n(n+1)/2\), која је реда \(\Theta(n^2)\). То је само дупло мање од вредности збира \(n + \ldots + n\), који се састоји од \(n\) сабирака и има вредност \(n^2\).
Збир \(n\) сабирака \(\log{1} + \ldots + \log{n}\) има вредност која се понаша као \(n\log{n} - n\), што је асимптотски исто као вредност збира \(\log{n} + \ldots + \log{n}\) који има \(n\) сабирака и вредност \(n\log{n}\).
Слично, збир \(1^2 + \ldots + n^2\) има вредност \(n(n+1)(2n+1)/6\), што је \(\Theta(n^3)\) и само је око три пута мање од збира \(n^2 + \ldots + n^2\) који има \(n\) сабирака и вредност \(n^3\).
Иако овакве генерализације прете да буду непрецизне, са малом дозом резерве се може проценити да алгоритми у којима се \(n\) пута примењује нека операција сложености \(\Theta(f(k))\) имају сложеност \(\Theta(n\cdot f(n))\), чак и када се операција у сваком кораку примењује над подацима који су се за \(O(1)\) повећали у односу на претходни корак и само у крајњој инстанци имамо \(\Theta(n)\) података.
Одмотавањем једначине \(T(n) = 2T(n-1) + O(1)\), \(T(0) = O(1)\) добијамо
\[\begin{eqnarray*} T(n) &=& 2T(n-1) + O(1)\\ &=& 2(2T(n-2) + O(1)) + O(1) = 4T(n-2) + 2O(1) + O(1)\\ &=& 4(2T(n-3)+O(1)) + 2O(1) + O(1)\\ &=& 8T(n-3) + 4O(1) + 2O(1) + O(1)\\ &=& \ldots\\ &=& 2^nT(0) + (2^{n-1} + \ldots + 2 + 1)\cdot O(1)\\ &=& 2^n\cdot O(1) + (2^n-1)\cdot O(1) = O(2^n). \end{eqnarray*}\]
Дакле, иако се у сваком рекурзивном позиву ради мало посла, рекурзивних позива има експоненцијално много, што доводи до изразито неефикасног алгоритма.
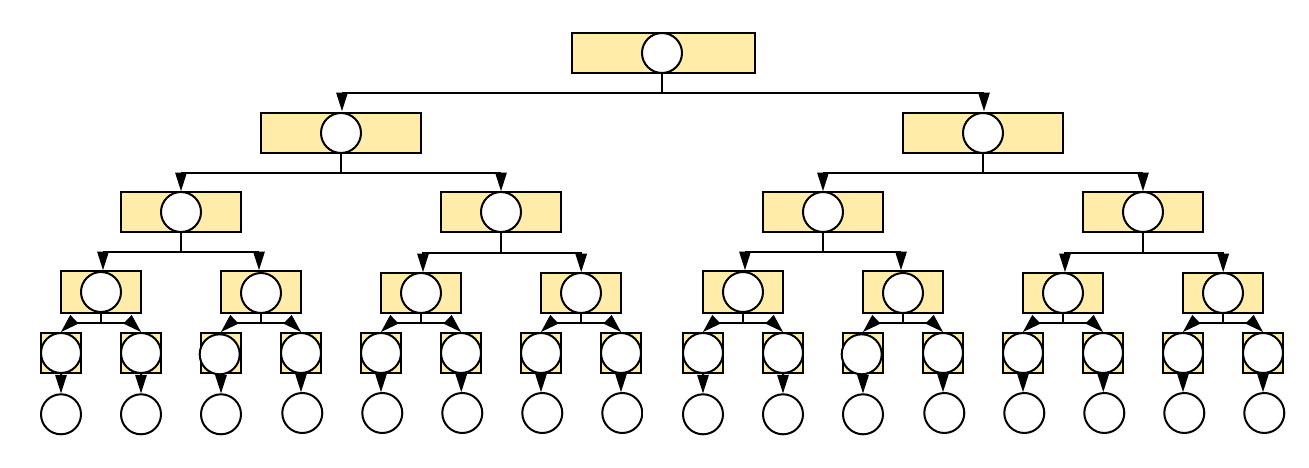
Функције које задовољавају једначину \(T(n) = 2T(n-1) + O(n)\), \(T(0) = O(1)\) такође показују експоненцијалну сложеност.
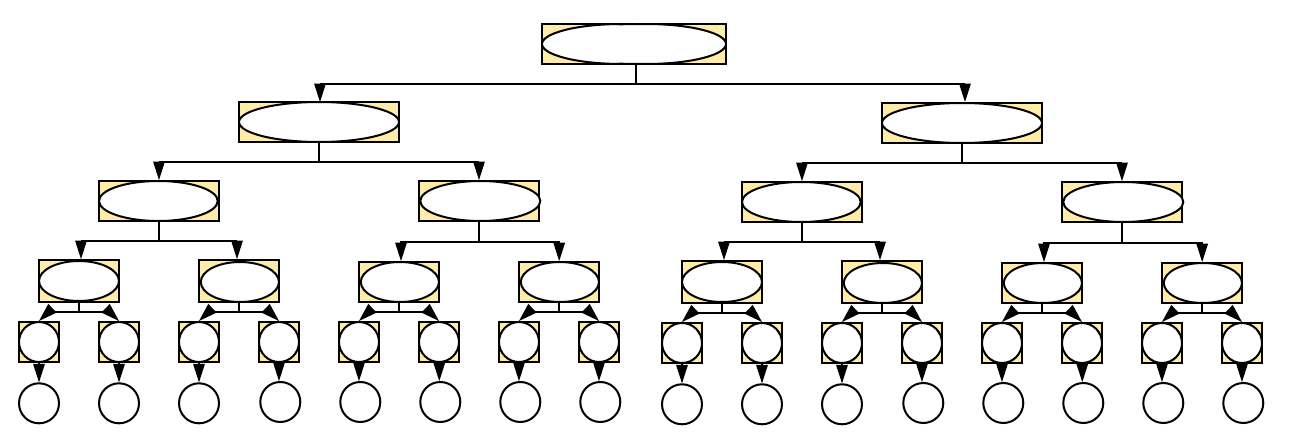
Одмотавањем једначине \(T(n) = 2T(n-1) + c\cdot n\), \(T(0) = O(1)\) добијамо
\[\begin{eqnarray*} T(n) &=& 2T(n-1) + c\cdot n\\ &=& 2(2T(n-2) + c\cdot (n-1)) + c\cdot n = 4T(n-2) + c\cdot (2 (n-1) + n)\\ &=& 4(2T(n-3)+ c\cdot (n-2)) + c\cdot (2 (n-1) + n)\\ &=& 8T(n-3) + c\cdot(4(n-2) + 2(n-1) + n)\\ &=& \ldots\\ &=& 2^nT(0) + c(2^{n-1}\cdot 1 + 2^{n-2}\cdot 2 + \ldots + 2(n-1) + n)\cdot O(1)\\ &=& 2^n\cdot O(1) + \sum_{k=0}^{n}2^k(n-k). \end{eqnarray*}\]
Коришћењем раније изведених формула можемо једноставно израчунати и суму
\[\sum_{k=0}^{n} 2^{k}(n-k) = n + 2(n-1) + 2^2(n-2) + \ldots + 2^{n-1}\cdot 1.\]
Важи да је
\[\begin{eqnarray*} \sum_{k=0}^{n} 2^{k}(n-k) &=& n\sum_{k=0}^{n}2^k - \sum_{k=0}^{n}k2^k\\ &=& n(2^{n+1}-1) - ((n-1)2^{n+1}+2)\\ &=& 2^{n+1}-n-2 \end{eqnarray*}\]
Зато је \(T(n) = 2^n\cdot O(1) + 2^{n+1}-n-2\). Дакле, и у овом случају функција показује експоненцијално понашање \(O(2^n)\).
Једначине засноване на декомпозицији проблема на неколико мањих потпроблема које су облика \(T(n) = aT(n/b) + O(n^k)\), \(T(0) = O(1)\) се решавају на основу мастер теореме.
Теорема: Решење рекурентне релације \(T(n) = aT(n/b)+cn^k\), где су \(a\) и \(b\) целобројне константе такве да важи \(a \geq 1\) и \(b \geq 1\), и \(c\) и \(k\) су позитивне реалне константе је
\[T(n)=\left\{ \begin{array}{ll} \Theta(n^{\log_b a}) \;,\; & \mbox{ако је} \log_b{a}>k\\ \Theta(n^k \log n) \;,\; & \mbox{ако је} \log_b{a}=k\\ \Theta(n^k) \;,\; & \mbox{ако је} \log_b{a}<k \end{array} \right.\]
Пре доказа ове теореме покушајмо опет да дамо неко интуитивно јасно објашњење.
У првом случају се добија дрво рекурзивних позива чији број чворова доминира послом који се ради у сваком чвору. Размотримо, на пример, једначину \(T(n) = 2\cdot T(n/2) + O(1)\), \(T(1) = O(1)\). Дрво ће садржати \(O(n)\) чворова, а у сваком чвору ће се вршити посао који захтева \(O(1)\) операција. Одмотавањем рекурентне једначине, добијамо
\[\begin{eqnarray*} T(n) &=& 2\cdot T(n/2) + O(1)\\ &=& 4\cdot T(n/4) + 2\cdot O(1) + O(1)\\ &=& 8\cdot T(n/8) + 4\cdot O(1) + 2 \cdot O(1) + O(1)\\ &=& 2^k \cdot T(n/2^k) + (2^{k-1} + \ldots + 2 + 1)\cdot O(1). \end{eqnarray*}\]
Ако је \(n=2^k\) добијамо да је \(n/2^k = 1\), па пошто је на основу формуле за збир геометријског низа \(2^{k-1} + \ldots + 2 + 1 = 2^k - 1\), сложеност је \(\Theta({n})\). И када \(n\) није степен двојке, добија се исто асимптотско понашање (што се може доказати ограничавањем одозго и одоздо степенима двојке).
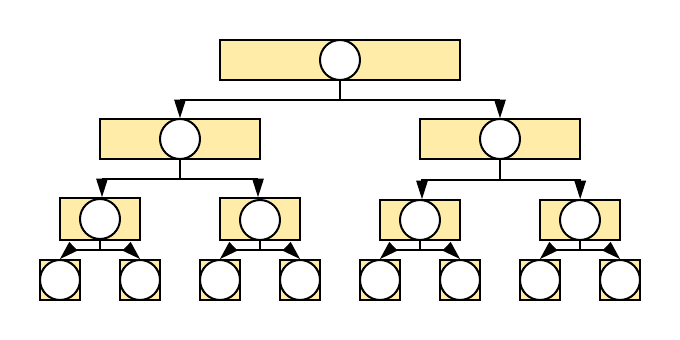
У другом случају су број чворова и посао који се ради на неки начин уравнотежени. Размотримо, на пример, једначину \(T(n) = 2\cdot T(n/2) + c\cdot n\), \(T(1) = O(1)\) и поново покушајмо да је одмотамо.
\[\begin{eqnarray*} T(n) &=& 2\cdot T(n/2) + c\cdot n\\ &=& 2\cdot(2\cdot T(n/4) + c\cdot n/2) + c\cdot n\\ &=& 4T(n/4) + c\cdot n + c\cdot n\\ &=& 4(2T(n/8) + c\cdot n/4) + 2\cdot c\cdot n\\ &=& 8T(n/8) + 3\cdot c\cdot n\\ &=& \ldots\\ &=& 2^k\cdot T(n/2^k) + k\cdot c\cdot n. \end{eqnarray*}\]
Ако је \(n=2^k\) после \(k = \log_2{n}\) корака \(n/2^k\) ће достићи вредност \(1\) тако да ће збир бити реда величине \(n\cdot O(1) + \log_2{n}\cdot c\cdot n = \Theta(n\log{n})\). Исто важи и када \(n\) није степен двојке.
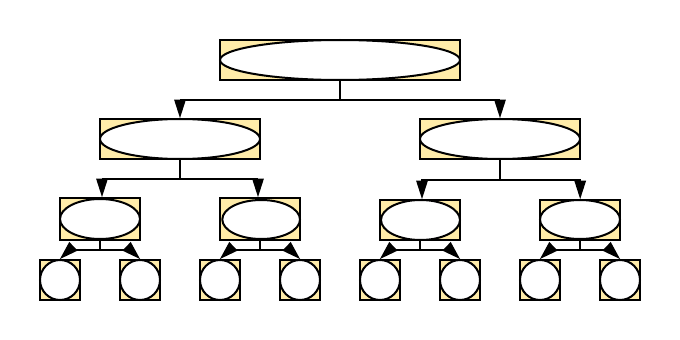
У трећем случају посао који се ради у чворовима доминира бројем чворова. Размотримо једначину \(T(n) = T(n/2) + cn\), \(T(1) = O(1)\). Њеним одмотавањем добијамо да је
\[\begin{eqnarray*} T(n) &=& T(n/2) + cn\\ &=& T(n/4) + cn/2 + cn\\ &=& T(n/8) + cn/4 + cn/2 + cn\\ &=& \ldots\\ &=& T(n/2^k) + cn(1/2^{k-1} + \ldots + 1/2 + 1). \end{eqnarray*}\]
Поново, ако је \(n=2^k\), тада је први члан једнак \(O(1)\) и пошто је на основу формуле за збир геометријског низа \(1/2^{k-1} + \ldots + 1/2 + 1 = (1 - (1/2)^k)/(1-(1/2)) = 2 - 2/n\) збир је једнак \(O(1) + cn(2-2/n) = \Theta(n)\).
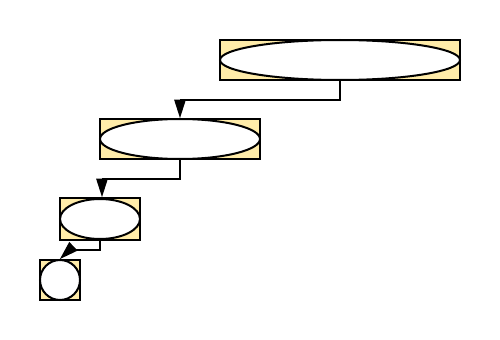
Прокоментаришимо да се у неким проблемима добијају једначине које нису баш у сваком рекурзивном позиву идентичне овим наведеним. На пример, приликом анализе алгоритма QuickSort, ако је пивот тачно на средини низа, важи да је \(T(n) = 2T(n/2) + O(n)\) и \(T(1) = O(1)\). Када би се то стално догађало, решење би било \(T(n) = O(n\log{n})\), међутим, вероватноћа да се то догоди је страшно мала, јер у већини случајева пивот не дели низ на два дела потпуно исте димензије и зато треба бити обазрив. Ако би се десило да пивот стално завршавао на једном крају низа, једначина би била \(T(n) = T(n-1) + O(n)\), \(T(1) = O(1)\), што би довело до сложености \(O(n^2)\), што и јесте сложеност најгорег случаја. Анализом коју ћемо приказати касније се може утврдити да је просечна сложеност \(O(n\log{n})\) тј. да иако пивот није стално на средини, да је у довољном процену случајева негде близу ње (рецимо између 25% и 75% дужине низа). Слична анализа важи и за проблем проналажења медијане.
Међутим, постоје и алгоритми код којих ствари стоје другачије. Приликом обиласка бинарног дрвета, балансираност нема утицаја. Наиме, ако је дрво потпуно, тада је једначина \(T(n) = 2T(n/2) + O(1)\), \(T(1) = O(1)\), чије је решење \(O(n)\). Међутим, чак и када је дрво издегенерисано у листу, једначина је \(T(n) = T(n-1) + O(1)\), \(T(1) = O(1)\), чије је решење опет \(O(n)\). Какав год да је однос броја чворова у левом и десном поддрвету решење ће бити \(O(n)\). То се може описати једначином \(T(n) = T(k) + T(n-k-1) + O(1)\), \(T(1) = O(1)\), за \(0 \leq k \leq n-1\), чије ће решење бити \(O(n)\), без обзира на то какво се \(k\) појављује у разним рекурзивним позивима.
Доказаћемо мастер теорему за једначину \(T(n) = aT(\frac{n}{b}) + cn^k\), \(T(1) = O(1)\), вредности \(n=b^m\), за \(m \in \mathbb{N}_0\). Једначина тада гласи:
\[T(b^m) = aT(b^{m-1}) + cb^{mk}\]
Да би се она лакше решил, можем да је поделимо са \(c\cdot a^m\) и добијамо
\[\frac{T(b^m)}{c\cdot a^m} = \frac{T(b^{m-1})}{c\cdot a^{m-1}} + \left(\frac{b^k}{a}\right)^m\]
Сада можемо увести смену \(t_m = \frac{T(b^m)}{c\cdot a^m}\) и \(q = \frac{b^k}{a}\), чиме добијамо једначину
\[t_m = t_{m-1} + q^m\]
Она се лако решава одмодавањем:
\[t_m = t_0 + \sum_{i=1}^m q^i,\]
где је \(t_0 = \frac{1}{c}T(1) = O(1)\).
За \(q\neq 1\) можемо применити формулу за збир геометријског реда,
\[t_m = t_0 + \left(\frac{q^{m+1} - 1}{q - 1} - 1\right),\]
док за \(q=1\) добијамо решење:
\[t_m = t_0 + m.\]
Зато је асимптотско понашање решења једнако:
\[t_m = \begin{cases} O(1),\qquad q < 1\\ O(m),\qquad q = 1,\\ O(q^m),\qquad q > 1 \end{cases}\]
Враћајућии смену добијамо
\[T(n) = T(b^m) = ca^mt_m = \begin{cases} O(a^m) = O(b^{m\log_b a})=O(n^{\log_b a}),\qquad a > b^k\\ O(ma^m)=O(\log_b n\cdot n^{\log_b a})=O(n^k \log n),\qquad a = b^k,\\ O((aq)^m)=O(b^{mk})=O(n^k),\qquad a < b^k \end{cases} \]