Понашање за конкретне вредности улазних параметара се може експериментално одредити, тестирањем рада програма. На пример, размотримо наредна два алгоритма (дата у псеудокоду) који израчунавају збирове природних бројева од \(1\) до \(i\), за свако \(i\) из интервала \(1\) до \(n\).
zbir = 0
foreach i in [1, n]:
zbir += i
print(zbir)и
function zbir(k):
zbir = 0
foreach i in [1, k]:
zbir += i
return zbir
foreach k in [1, n]:
print(zbir(k))Ако се први алгоритам имплементира (на пример, у програмском језику Python) и ако се измери његово време извршавања за различите вредности \(n\), добијају се следећи резултати (као резултат приказан је збир свих бројева од \(1\) до \(n\)).
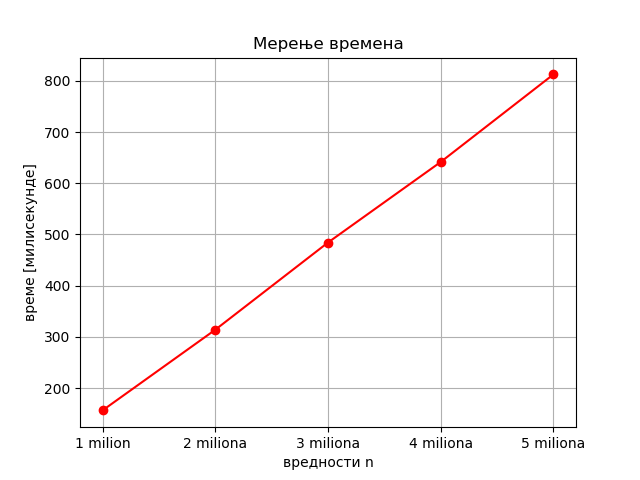
n = 1000000, rezultat: 500000500000, vreme: 0.16 sekundi n = 2000000, rezultat: 2000001000000, vreme: 0.31 sekundi n = 3000000, rezultat: 4500001500000, vreme: 0.49 sekundi n = 4000000, rezultat: 8000002000000, vreme: 0.65 sekundi n = 5000000, rezultat: 12500002500000, vreme: 0.83 sekundi
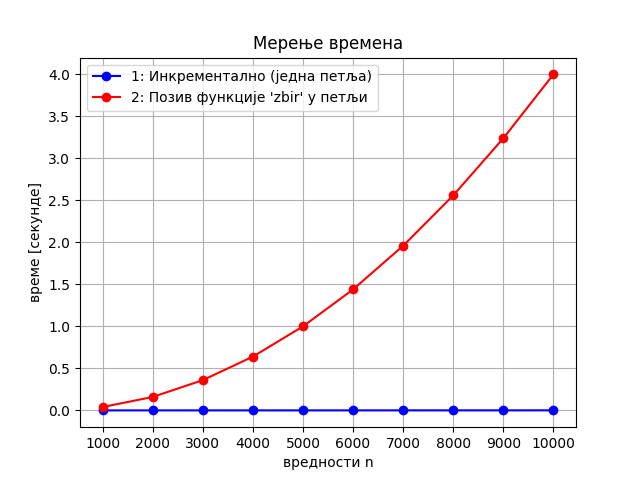
Већ одавде се види да су времена приближно сразмерна вредностима \(n\). Још прегледнији начин да уочимо ову пропорционалност је приказивање графика времена израчунавања суме у зависности од \(n\), са кога се јасно види да код првог програма време извршавања приближно линеарно зависи од \(n\).

Ако се други алгоритам имплементира и ако се измери његово време извршавања (на пример, у програмском језику Python), добијају се следећи резултати (поново је приказан само збир свих бројева од \(1\) до \(n\)).
n = 1000, rezultat: 500500, vreme: 31.24 ms n = 2000, rezultat: 2001000, vreme: 156.25 ms n = 3000, rezultat: 4501500, vreme: 359.35 ms n = 4000, rezultat: 8002000, vreme: 633.19 ms n = 5000, rezultat: 12502500, vreme: 993.25 ms n = 6000, rezultat: 18003000, vreme: 1448.38 ms n = 7000, rezultat: 24503500, vreme: 1984.94 ms n = 8000, rezultat: 32004000, vreme: 2547.53 ms n = 9000, rezultat: 40504500, vreme: 3291.45 ms n = 10000, rezultat: 50005000, vreme: 4049.11 ms
У овом случају зависност није линеарна. Наиме, када се \(n\) удвостручи, време се уместо 2 пута, отрпилике увећа 4 пута, што сугерише да је време извршавања сразмерно са квадратом величине улаза, тј. да је у питању квадратна зависност. Рачунањем \(\frac{t(n)}{n^2}\) за разне \(n\) добијамо приближно сталну вредност 0.00004, што значи да се време извршавања \(t(n)\) може апроксимирати као \(t(n) \approx 0.00004 n^2\). На следећој слици видимо график измерених вредности и график вредности добијене квадратне функције која моделира време извршавања.
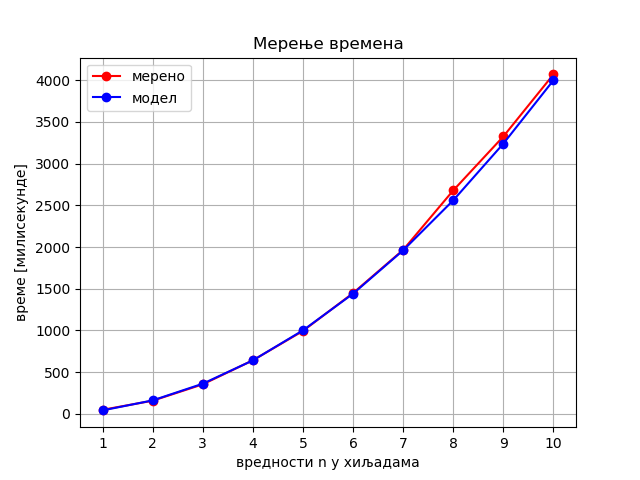
Два дата графика се у значајној мери поклапају, што показује да је \(0.00004 n^2\) веома добра процена времена извршавања алгоритма за разне вредности \(n\). Наравно, време извршвања увек зависи од програмског језика и конкретног рачунара на ком је мерење извршено, али експеримент говори да можемо очекивати да ће време рада другог алгоритма увек бити прилижно квадратна функција величине улаза. Ово се, наравно, може и формално доказати анализом броја извршених инструкција.
На основу измерених времена видимо да је први програм неупоредиво бржи у односу на други. Линеарно време извршавања је толико мање од квадратног, да када се оба времена прикажу на истом графику, делује да је линеарно време стално једнако нули.