Да бисмо могли да анализирамо сложеност потребно је да владамо одређеним математичким апаратом. У наставку ћемо резимирати основне математичке појмове које ћемо користити у анализи сложености алгоритама.
Током анализе алгоритама често имамо потребу да израчунамо одређене коначне суме. Са њима сте се сретали у средњој школи и курсевима дискретне математике. Резимирајмо их кроз неколико најзначајнијих примера.
Гаусу се приписује да је још као дете израчунао да је
\[1 + 2 + \ldots + n = \sum_{k=0}^{n} k = \frac{n(n+1)}{2}.\]
Заиста, у овом збиру се крије \(n/2\) парова чији је збир \(n+1\) (ово, наравно, важи само када је \(n\) паран број, али нам даје одличну интуицију која нам помаже да ову формулу лако запамтимо). Прецизније, ако означимо тај збир са \(S\) онда је \(2S = S+S = (1 + 2 + \ldots + n) + (n + (n-1) + \ldots + 1) = n\cdot(n+1)\).
Некада слика говори више од речи.

На основу претходног једноставно се изводи да је збир првих \(n\) чланова аритметичког низа чији је први члан \(a\), а разлика између свака два суседна члана једнака \(р\) једнака
\[a + (a + r) + (a + 2r) + \ldots + (a + (n-1)\cdot r) = \sum_{k=0}^{n-1} (a + k\cdot r) = n\cdot a + r\frac{n(n-1)}{2}.\]
Интуиција нам опет говори да се овде крије \(\frac{n}{2}\) парова чији је збир \(a_0 + a_{n-1}\), што опет доводи до формуле \(\frac{n}{2}\left(2a + (n-1)\cdot r\right)\).
Један важан аритметички низ је низ непарних бројева. Важи да је \(1 + 3 + 5 + \ldots + (2k-1) = \frac{k}{2} \cdot (1 + (2k-1)) = k^2\).
Израчунавање збира узастопних парних бројева се лако своди на збир узастопних бројева. \(2 + 4 + 6 + \ldots 2k = 2(1+2+3+\ldots k) = k(k+1)\).
Поново слика говори више од речи.
Изведимо формулу за збир првих \(n\) чланова геометријског низа коме је први члан \(a\) а количник свака два узастопна члана \(q \neq 1\). Обележимо тражену суму са \(S\).
\[S = a + a \cdot q^1 + a \cdot q^2+ \ldots + a \cdot q^{n-2} + a \cdot q^{n-1} = \sum_{k=0}^{n-1} a\cdot q^k.\]
Ако леву и десну страну претходне једнакости помножимо са \(1 - q\) добијамо једнакост:
\(S \cdot (1 - q) = a \cdot (1 - q) + a \cdot q \cdot (1 - q) + a \cdot q^2 \cdot (1 - q) + \ldots + a \cdot q^{n-2}\cdot (1 - q) + a \cdot q^{n-1} \cdot (1 - q)\)
Извршимо множења на десној страни једнакости:
\[S \cdot (1 - q) = a - a\cdot q + a \cdot q - a \cdot q^2 + a \cdot q^2 - a \cdot q^3 + \ldots + a \cdot q^{n-2} - a \cdot q^{n-1} + a \cdot q^{n-1} - a \cdot q^n\]
Сређивањем последњег израза добијамо \(S \cdot (1 - q) = a - a \cdot q^n\). Према томе, пошто је \(q \neq 1\), важи
\[S = a \cdot \frac {1 - q^n}{1 - q}.\]
За \(|q| < 1\) геометријски ред конвергира и сума му је \(\frac{a}{1-q}\).
Нама ће најчешће бити корисни случајеви \(q=2\) и \(q=1/2\).
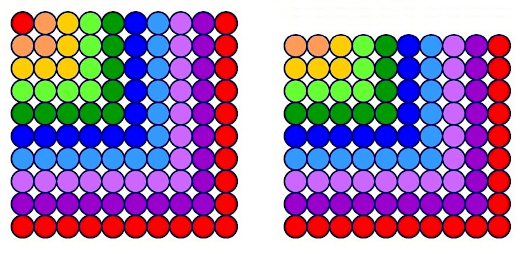
На основу претходне формуле, за \(a=1\) и \(q=2\), важи да је \(1+2+\ldots+2^{n-1} = 2^n - 1\). Ова формула има интересантно тумачење. Сума са леве стране представља укупан број чворова на првих \(n\) нивоа потпуног бинарног дрвета, док је израз са десне стране за један мањи од броја чворова на наредном нивоу \(n+1\). Дакле, на сваком наредном нивоу бинарног дрвета има један чвор више него што је чворова на свим претходним нивоима дрвета.
За \(a=1\) и \(q=1/2\) добијамо да је
\[1+1/2+\ldots+(1/2)^{n-1} = \frac{1-(1/2)^n}{1-1/2} = 2-(1/2)^{n-1}.\]
Са порастом \(n\) ова вредност се приближава вредности \(2\) (свакако је њоме ограничена одозго).
Опет слика говори више од речи.
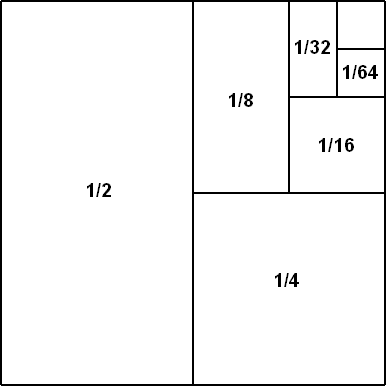
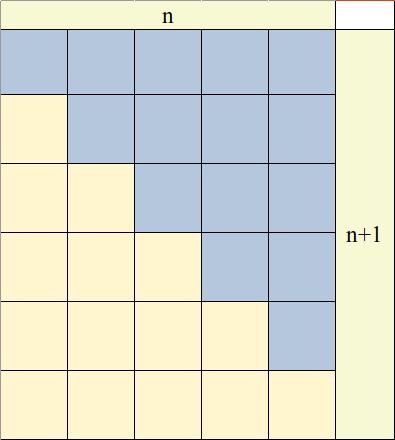
Прикажимо како можемо израчунати суму квадрата свих природних бројева од \(1\) до \(n\). Важи да је
\[(k+1)^3 - k^3 = k^3 + 3k^2 + 3k + 1 - k^3 = 3k^2 + 3k + 1.\]
Зато је \[\begin{eqnarray*} 2^3 - 1^3 &=& 3\cdot 1^2 + 3\cdot 1 + 1\\ 3^3 - 2^3 &=& 3\cdot 2^2 + 3\cdot 2 + 1\\ \ldots\\ (n+1)^3 - n^3 &=& 3\cdot n^2 + 3\cdot n + 1 \end{eqnarray*}\]
Сабирањем претходних једнакости добијамо
\[(n+1)^3 - 1 = 3\cdot(1^2+\ldots + n^2) + 3\cdot(1+\ldots+n) + (1+\ldots + 1)\]
тј.
\[3\cdot \sum_{k=1}^{n} k^2 = (n+1)^3-1 - 3\sum_{k=1}^{n} k - \sum_{k=1}^{n} 1.\]
На основу раније изведених формула за збир аритметичког низа, следи да је
\[\sum_{k=1}^n k^2 = \frac{1}{3}\cdot\left(n^3 +3n^2 +3n - 3\frac{n(n+1)}{2} - n\right) = \frac{n\cdot (2n+1)\cdot (n+1)}{6} = \frac{1}{3}\left(n \cdot (n + \frac{1}{2}) \cdot (n+1)\right).\]
Дакле, сума квадрата природних бројева од \(1\) до \(n\) се асимптотски понаша као \(\frac{n^3}{3}\).
Опет слика говори више од речи.
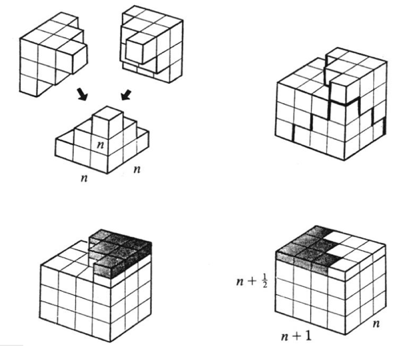
Потпуно аналогно, сумирањем израза \((k+1)^4 - k^4\) од \(1\) до \(n\) и применом до сада изведених формула може се показати да је
\[1^3+2^3+\ldots + n^3 = \sum_{k=1}^n k^3 = \frac{(n(n+1))^2}{4}.\]
Ово тврђење, познато као Никомахова теорема показује да је збир кубова свих природних бројева од \(1\) до \(n\) једнак квадрату збира свих природних бројева од \(1\) до \(n\) и асимптотски се понаша као \(\frac{n^4}{4}\).
Опет слика говори више од речи.
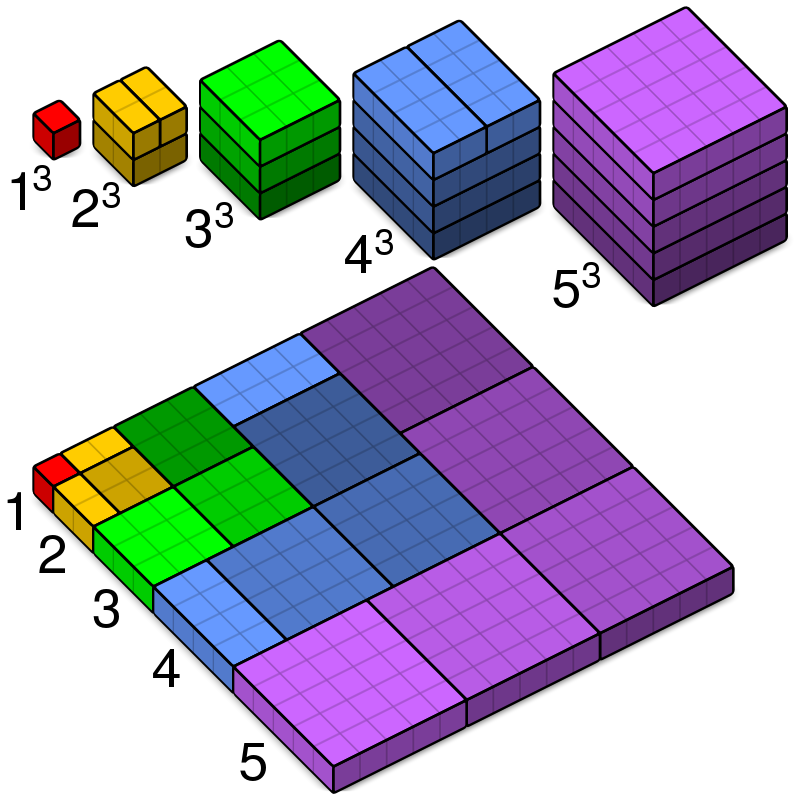
Пошто ће нас у анализи алгоритама најчешће занимати само асимптотско понашање функција, најважније је запамтити да се сума \(n\) \(p\)-тих степена свих природних бројева од \(1\) до \(n\) асимптотски понаша као \(\frac{n^{p+1}}{p+1}\).
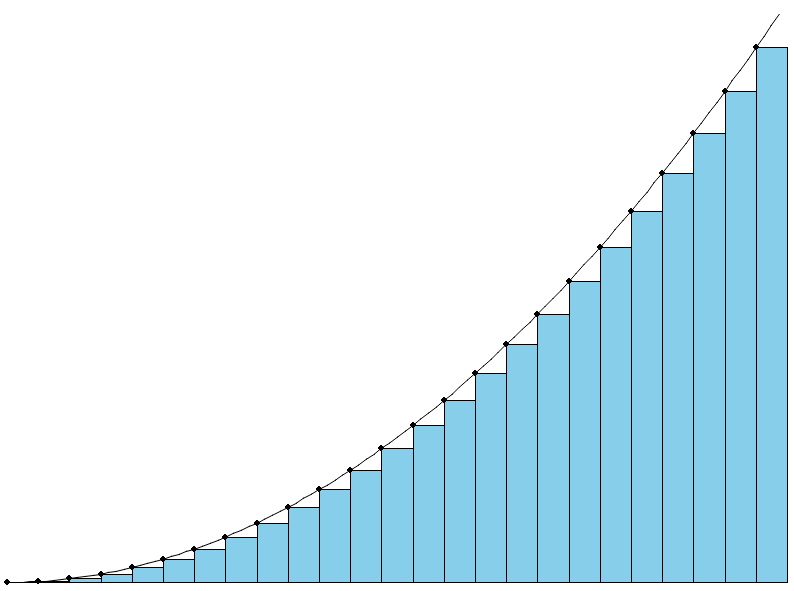
За израчунавање и оцену сума могу се користити и изводи и интеграли. Приметимо да је неодређени интеграл функције \(x^p\) функција \(\frac{x^{p+1}}{p+1}\), а да се збир \(p\)-тих степена свих природних бројева од \(1\) до \(n\) асимптотски понаша управо као \(\frac{n^{p+1}}{p+1}\). То није случајност. Размотримо монотоно растућу функцију \(f\) (таква је функција \(f(x)=x^n\)) на домену \(x \geq 0\). Сума \(\sum_{k=0}^{n-1} f(k)\) се визуелно може представити као површина \(n\) правоугаоника (свакоме је ширина \(1\), а висина \(k\)-тог је \(f(k)\)). На слици је приказана сума првих \(25\) потпуних квадрата. Са слике је прилично очигледно да је та сума (збир површина правоугаоника) веома блиска површини испод криве \(f(x) = x^2\) која се може израчунати (тј. чије се асимптотско понашање може проценити) применом одређених интеграла.
Илуструјмо ово и мало прецизније. Површина испод криве \(f(x)\) за \(k \leq x \leq k+1\) једнака је одређеном интегралу \(\int_{k}^{k+1} f(x)\ dx\). Пошто је функција растућа, та површина је већа од површине правоугаоника чија је висина \(f(k)\) и ширина \(1\), а мања од површине правоугаоника чија је висина \(f(k+1)\) и ширина \(1\) тј. важи
\[f(k) \leq \int_k^{k+1} f(x)\ dx \leq f(k+1).\]
Зато је
\[\sum_{k=0}^{n-1} f(k) \leq \int_0^{n} f(x)\ dx \leq \sum_{k=0}^{n-1} f(k+1).\]
Горњу границу суме можемо директно прочитати из прве неједнакости. Пошто је
\[\sum_{k=0}^{n-1} f(k+1) = \sum_{k=0}^{n-1} f(k) - f(0) + f(n),\]
из друге неједнакости следи и доња граница, па важи:
\[\int_{0}^n f(x)\ dx + f(0) - f(n) \leq \sum_{k=0}^{n-1} f(k) \leq \int_0^n f(x)\ dx.\]
Случај када је \(f(x)\) монотоно опадајућа функција за \(x \geq 0\) се обрађује аналогно (само је потребно уместо \(\leq\) користити \(\geq\)).
На пример, понашање суме \(\sum_{k=0}^{n-1} ka^k = a + 2a^2 + 3a^3 + \ldots + (n-1)a^{n-1},\) можемо проценити израчунавањем одређеног интеграла \(\int_0^n xa^x\ dx.\)
Он се једноставно може израчунати парцијалном интеграцијом за \(u=x\) (па је \(du=dx\)) и \(dv=a^x\ dx\), одакле је \(v = \frac{a^x}{\ln{a}}\). Зато је
\[\int_0^n xa^x\ dx = \int_0^n u\ dv = (uv)\big\rvert_0^n - \int_{0}^n v\ du = \frac{na^n}{\ln{a}} - \frac{\int_0^n a^x\ dx}{\ln{a}} = \frac{na^n}{\ln{a}} - \frac{(a^n - 1)}{\ln^2{a}},\]
па се ова функција асимптотски понаша као \(na^n\).
Ову суму је могуће израчунати и егзактно, применом диференцирања. Наиме, важи да је
\[\sum_{k=0}^{n-1} x^k = 1 + x + \ldots + x^{n-1} = \frac{x^n - 1}{x-1}.\]
Диференцирањем обе стране по \(x\) добијамо
\[1 + 2x + 3x^2 + \ldots + (n-1)x^{n-2} = \frac{nx^{n-1}(x-1) - (x^n-1)}{(x-1)^2}.\]
Множењем са \(x\) добијамо
\[\sum_{k=0}^{n-1} kx^k = x + 2x^2 + 3x^3 + \ldots + (n-1)x^{n-1} = x\frac{nx^{n-1}(x-1) - (x^n-1)}{(x-1)^2}.\]
На пример, за \(x=2\) добијамо да је \(\sum_{k=0}^{n-1} k2^k = (n-2)\cdot 2^{n} + 2\).
Напоменимо и да се та сума веома једноставно може израчунати и сасвим елементарним техникама. Нека је \(S_x(n) = \sum_{k=0}^{n-1} kx^k\). Тада множењем ове једнакости са \(x\), одузимањем добијеног резултата од полазне једнакости и применом формуле за збир геометријског низа добијамо
\[\begin{eqnarray*} S_x(n) &=& x^1 + 2x^2 + 3x^3 + \ldots + (n-2)x^{n-2} + (n-1)x^{n-1}\\ x\cdot S_x(n) &=& x^2 + 2x^3 + 3x^4 + \ldots + (n-2)x^{n-1} + (n-1)x^n\\ S_x(n) - xS_x(n) &=& x^1 + x^2 + x^3 + \ldots + x^{n-1} + (n-1)x^n\\ (1 - x)S_x(n) &=& x(x^0 + \ldots + x^{n-2}) + (n-1)x^n = x\frac{1-x^{n-1}}{1-x} + (n-1)x^n \end{eqnarray*}\]
Одатле следи да је
\[S_x(n) = \frac{x-x^n}{(1-x)^2} + (n-1)x^n\]
Иако није добијен идентичан израз ономе који је добијен применом диференцирања, лако се показује да су добијени изрази једнаки. Заменом вредности \(x=2\) поново добијамо да је \(S_2(n) = \sum_{k=0}^{n-1} k2^k = (n-2)\cdot 2^{n} + 2\).
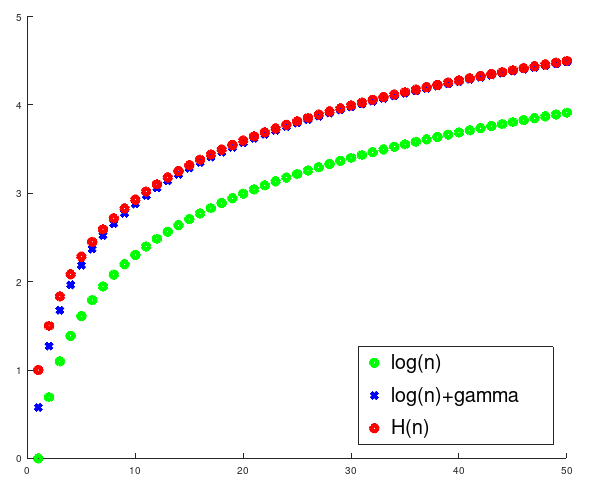
Размотримо збир \(H(n) = 1 + \frac{1}{2} + \frac{1}{3} + \frac{1}{4} + \ldots + \frac{1}{n}\). Њега не можемо егзактно израчунати, али можемо га прилично добро приближно проценити.
Прво покажимо да \(H(n)\) дивергира и да тежи бесконачности како \(n\) тежи бесконачности. Важи да је \(H(n) > 1 + \frac{1}{2} + \frac{1}{4} + \frac{1}{4} + \frac{1}{8} + \frac{1}{8} + \frac{1}{8} + \frac{1}{8} + \ldots\) Наиме, важи да је \(\frac{1}{3} > \frac{1}{4}\), затим да је \(\frac{1}{5} > \frac{1}{8}\), \(\frac{1}{6} > \frac{1}{8}\) и \(\frac{1}{7} > \frac{1}{8}\) итд. Међутим, важи да је \(\frac{1}{4} + \frac{1}{4} = \frac{1}{2}\), да је \(\frac{1}{8} + \frac{1}{8} + \frac{1}{8} + \frac{1}{8} = \frac{1}{2}\) итд. Зато је десни збир једнак \(1 + \frac{1}{2} + \frac{1}{2} + \frac{1}{2} + \ldots\), а овај збир јасно дивергира тј. тежи бесконачности са повећањем броја сабирака.
Слично би се могло доказати и коришћењем процене суме одређеним интегралом. Број \(H(n)\) се може проценити као \(\int_1^{n+1} \frac{1}{x}\mathrm{d}x\), који је једнак \((\ln{x})\big\rvert^{n+1}_1\) тј. \(\ln{(n+1)}\).
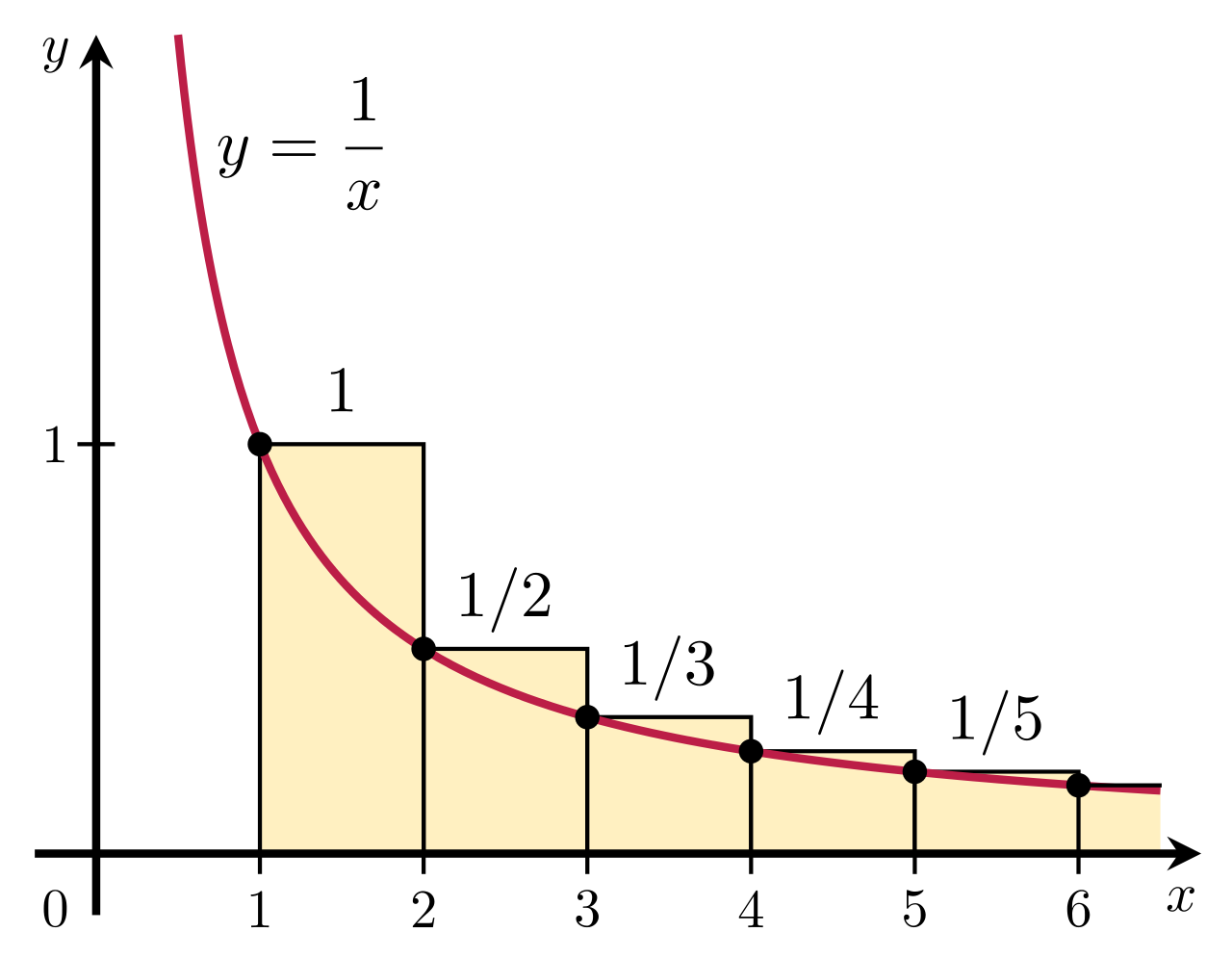
Ако се нацрта график функције \(H(n)\) може се уочити да она веома споро тежи бесконачности и може се приметити веома сличан облик графику функције \(\ln{n}\). Заиста, доказује се да разлика између функција \(H(n)\) и \(\ln{n}\) веома брзо конвергира и тежи константи \(\gamma\) која је позната под именом Ојлер-Маскеронијева константа и чија је вредност приближно једнака \(\gamma = 0.57722\). Ништа се не би променило и да се посматра однос \(H(n)\) са функцијом \(\ln{(n+1)}\) (јер са повећањем \(n\) разлика између \(\ln{(n+1)}\) и \(\ln{n}\) веома брзо тежи нули), осим што би процена била мало прецизнија за мале вредности \(n\).