Мерење времена извршавања се може урадити за сваки програм, али оно није поуздан аргумент само за себе, већ служи пре свега за почетно стицање осећаја о ефикасности појединих алгоритама (да знамо шта треба да докажемо), као и за потврду закључака добијених теоријским разматрањем. Осим тога, често нам је потребно да можемо да унапред дамо неку грубу процену потребних ресурса за произвољне улазне вредности, без покретања програма (па чак и пре писања програма, само на основу алгоритма који ће бити примењен).
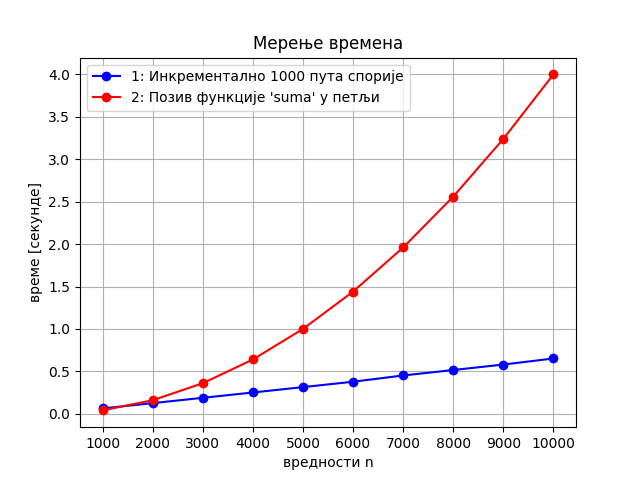
Питање које се природно поставља је то на ком ће се рачунару програм извршавати. Наравно, ако је један рачунар два пута бржи (у неком сегменту) од другог, за очекивати је да ће се програм на њему извршавати два пута брже. Ипак, показаће се да су разлике између ефикасних и неефикасних алгоритама толико велике, да је то што је неки рачунар 2, 3 или чак 10 пута бржи од другог заправо небитно и не може да надомести то колико је неефикасан алгоритам лошији од ефикасног. На пример, наредна слика приказује како би изгледао однос времена извршавања ако би се бржи алгоритам извршавао на 1000 пута споријем рачунару. Као што видимо, линеарна функција се мало “одлепила” од нуле, међутим, и даље су њене вредности много мање него код квадратне функције. Другим речима, алгоритам линеарне сложености, чак и када се успори 1000 пута, и даље је много бржи од алгоритма квадратне сложености (и што је \(n\) веће, разлика у брзини је све већа).

Да бисмо проценили зависност времена извршавања од димензије проблема, основни приступ је да покушамо да конструишемо функцију \(f(n)\) која одређује зависност броја инструкција које алгоритам треба да изврши у односу на величину улаза \(n\).
Израчунајмо број наредби сабирања које се изврше у првом и у другом програму из претходног примера (програми извршавају и друге наредбе, попут оних потребних да се организују петље, међутим, претпоставићемо да су нам сабирања једино значајна).
Јасно је да се у првом програму врши једно сабирање по петљи, па је укупан број сабирања једнак броју корака извршавања петље, а то је \(n\). Ово је линеарна зависност, што је у складу са измереним временима.
У другом програму анализа је мало компликованија. За било које дато \(k\), функција zbir врши око \(k\) сабирања. Пошто се функција позива за све вредности \(k\) од 1 до \(n\), то се укупно изврши \(1 + 2 + \ldots + n = \frac{n(n+1)}{2} = \frac{1}{2}n^2 + \frac{1}{2}n\) сабирања. И ако бисмо рачунали све инструкције, добили бисмо да је број инструкција нека квадратна функција облика \(an^2 + bn + c\), што је опет у складу са измереним временима.
Ако (поједностављено) претпоставимо да се свака инструкција на рачунару извршава за једну наносекунду (\(10^{-9}s\)), а да број инструкција зависи од величине улаза \(n\) на основу функције \(f(n)\), тада је време потребно да се алгоритам изврши дат у следећим табелама.
Алгоритми чија је сложеност одозго ограничена полиномијалним функцијама, у принципу се сматрају ефикасним.
| \(n / f(n)\) | \(\log{n}\) | \(\sqrt{n}\) | \(n\) | \(n\log{n}\) | \(n^2\) | \(n^3\) |
|---|---|---|---|---|---|---|
| 10 | 0,003 \(\mu s\) | 0,003 \(\mu s\) | 0,01 \(\mu s\) | 0,033 \(\mu s\) | 0,1 \(\mu s\) | 1 \(\mu s\) |
| 100 | 0,007 \(\mu s\) | \(0,010\) \(\mu s\) | 0,1 \(\mu s\) | 0,644 \(\mu s\) | 10 \(\mu s\) | 1 \(ms\) |
| 1,000 | 0,010 \(\mu s\) | \(0,032\) \(\mu s\) | 1,0 \(\mu s\) | 9,966 \(\mu s\) | 1 \(ms\) | 1 \(s\) |
| 10,000 | 0,013 \(\mu s\) | \(0,1\) \(\mu s\) | 10 \(\mu s\) | 130 \(\mu s\) | 0,1 \(s\) | 16,7 \(min\) |
| 100,000 | 0,017 \(\mu s\) | \(0,316\) \(\mu s\) | 100 \(\mu s\) | 1,67 \(ms\) | 10 \(s\) | 11,57 \(dan\) |
| 1,000,000 | 0,020 \(\mu s\) | 1 \(\mu s\) | 1 \(ms\) | 19,93 \(ms\) | 16,7 \(min\) | 31,7 \(god\) |
| 10,000,000 | 0,023 \(\mu s\) | 3,16 \(\mu s\) | 10 \(ms\) | 0,23 \(s\) | 1,16 \(dan\) | \(3\times 10^5\) \(god\) |
| 100,000,000 | 0,027 \(\mu s\) | 10 \(\mu s\) | 0,1 \(s\) | 2,66 \(s\) | 115,7 \(dan\) | |
| 1,000,000,000 | 0,030 \(\mu s\) | 31,62 \(\mu s\) | 1 \(s\) | 29,9 \(s\) | 31,7 \(god\) |
Алгоритми чија је сложеност одоздо ограничена експоненцијалном или факторијелском функцијом се сматрају неефикасним.
| \(n / f(n)\) | \(2^n\) | \(n!\) |
|---|---|---|
| 10 | 1 \(\mu s\) | 3,63 \(ms\) |
| 20 | 1 \(ms\) | 77,1 \(god\) |
| 30 | 1 \(s\) | \(8,4\times 10^{15}\) \(god\) |
| 40 | 18,3 \(min\) | |
| 50 | 13 \(dan\) | |
| 100 | \(4 \times 10^{13}\) \(god\) |
Можемо поставити и питање која димензија улаза се отприлике може обрадити за одређено време. Одговор је дат у наредној табели.
| \(t\) | \(n\) | \(n\log{n}\) | \(n^2\) | \(n^3\) | \(2^n\) | \(n!\) |
|---|---|---|---|---|---|---|
| \(1ms\) | \(10^6\) | \(63,000\) | \(1,000\) | \(100\) | \(20\) | \(9\) |
| \(10ms\) | \(10\cdot 10^6\) | \(530,000\) | \(3,200\) | \(215\) | \(23\) | \(10\) |
| \(100ms\) | \(100\cdot 10^6\) | \(4,5\cdot 10^6\) | \(10,000\) | \(465\) | \(27\) | \(11\) |
| \(1s\) | \(10^9\) | \(40\cdot 10^6\) | \(32,000\) | \(1,000\) | \(30\) | \(12\) |
| \(1min\) | \(60\cdot 10^{9}\) | \(1,9\cdot 10^9\) | \(245,000\) | \(3,900\) | \(36\) | \(14\) |
Из претходних табела јасно је да време извршавања суштински зависи од функције \(f(n)\). На пример, ако поредимо алгоритме код којих је \(f_1(n) = n\), \(f_2(n) = 5n\), \(f_3(n) = n^2\) и \(f_4(n) = 2n^2 + 3n + 2\), јасно нам је да ће се за \(n=10^6\), време извршавања првог и другог алгоритма мерити милисекундама, док ће се време извршавања трећег и четвртог алгоритма мерити минутима. Код функције \(f_4\), јасно је да је време које потиче од фактора \(3n\) (три милисекунде) и \(2\) (две нанонсекунде) апсолутно занемариво у односу на време које долази од фактора \(2n^2\) (око 33 минута). За прва два алгоритма рећи ћемо да имају линеарну временску сложеност, а за друга два да имају квадратну временску сложеност.
Чак ни педесет пута бржи рачунар неће помоћи да се трећи или четврти алгоритам изврше брже од првог или другог. Иако смо поједностављено претпоставили да се све инструкције извршавају исто време (једну наносекунду), што није случај у реалности, из претходних табела је јасно да нам тај поједностављени модел даје сасвим добру основу за поређење различитих алгоритама и да прецизнија анализа не би ни по чему значајно променила ситуацију. Сложеност се обично процењује на основу изворног кода програма. Савремени компилатори извршавају различите напредне оптимизације и машински кôд који се извршава може бити прилично другачији од изворног кода програма (на пример, компилатор може скупу операцију множења заменити ефикаснијим битовским операцијама, може наредбу која се више пута извршава у петљи изместити ван петље и слично). Детаљи који се у изворном коду не виде, попут питања да ли се неки податак налази у кеш-меморији или је потребно приступати РАМ-у, такође могу веома значајно да утичу на стварно време извршавања програма. Савремени процесори подржавају проточну обраду и паралелно извршавање инструкција, што такође чини стварно понашање програма другачијим од класичног, секвенцијалног модела који се најчешће подразумева приликом анализе алгоритама. Дакле, стварно време извршавања програма зависи од карактеристика конкретног рачунара на ком се програм извршава, али и од карактеристика програмског преводиоца, па и оперативног система на ком се програм извршава. Међутим, поново наглашавамо да ништа од тих фактора не може променити однос између времена извршавања алгоритама линеарне и алгоритама квадратне сложености, за велике улазе (код малих улаза, сви алгоритми раде веома ефикасно, па нам обрада малих улаза није интересантна).
Дакле, можемо закључити да нам за је за грубу процену времена потребног за извршавање неког алгоритма, чији број инструкција полиномијално зависи од величине улаза \(n\) довољно да знамо само који је степен тог полинома. Можемо слободно да занемаримо све мономе мањег степена, а можемо и слободно да занемаримо коефицијенте уз водећи степен, као и коефицијент којим се одређује брзина стварног рачунара у односу на овај фиктивни, за који смо приказали времена. Наиме у реалним ситуацијама сви ти коефицијенти могу да утичу да ће програм бити бржи или спорији највише десетак пута (па нек је и стотинак пута), али не могу да утичу на то да се за велики улаз алгоритам чији је број инструкција квадратни изврши брже од алгоритма чији је број инструкција линеаран (говоримо о односу минута и милисекунди).
Горња граница сложености се обично изражава коришћењем \(O\)-нотације.
Дефиниција: Ако постоје позитивна реална константа \(c\) и природан број \(n_0\) такви да за функције \(f\) и \(g\) над природним бројевима важи \(f(n) \leq c \cdot g(n)\) за све природне бројеве \(n\) веће од \(n_0\) онда пишемо \(f(n)=O(g(n))\) и читамо “\(f\) је велико ,о` од \(g\)”.
У неким случајевима користимо и ознаку \(\Theta\) која нам не даје само горњу границу, већ прецизно описује асимптотско понашање.
Дефиниција: Ако постоје позитивне реалне константе \(c_1\) и \(c_2\) и природан број \(n_0\) такви да за функције \(f\) и \(g\) над природним бројевима важи \(c_1 \cdot g(n) \leq f(n) \leq c_2 \cdot g(n)\) за све природне бројеве \(n\) веће од \(n_0\), онда пишемо \(f(n)=\Theta(g(n))\) и читамо ,,\(f\) је велико ‘тета’ од \(g\)``.
Дакле, асимптотским ознакама смо занемарили мономе мањег степена и сакрили константе уз највећи степен полинома. Стварно време извршавања зависи и од константи сакривених у асимптотским ознакама, међутим, асимптотско понашање обично прилично добро одређује његов ред величине (да ли су у питању микросекунде, милисекунде, секунде, минути, сати, дани, године).
Наведимо карактеристике основних класа сложености.
Иако су класе поређане редом, не треба претпостављати да су оне “подједнако размакнуте”. На пример, честа је заблуда да су алгоритми сложености \(O(n \log{n})\) по својој ефикасности негде између \(O(n)\) и \(O(n^2)\). Истина је заправо да су они прилично слични класи \(O(n)\) и да је често тешко емпријски измерити разлику између те две класе, а да су и једни и други неупоредиво бржи од алгоритама квадратне сложености. На пример, ако је \(n=10^6\), веома груба процена (када се занемаре сви константни коефицијенти) броја корака линеарног алгоритма је \(10^6\), квазилинеарног алгоритма је око \(20 \cdot 10^6\), а број корака квадратног алгоритма је \(10^{12}\). Дакле, на тако великом улазу квазилинеарни алгоритам би био тек пар десетина пута спорији од линеарног (конкретан однос, наравно, зависио би од констаних фактора), док би квадратни алгоритам био милион пута спорији од линеарног и неких педесет хиљада пута спорији од квазилинеарног.