Hofmanov i Grejov kod

Hofmanovo kodiranje je algoritam kodiranja za kompresiju podataka koji pronalazi optimalni sistem kodiranja objekata zasnovan na relativnoj frekvenciji pojave svakog objekta u kolekciji.


Danas taj kod ima veliku primenu. U pitanju je optimalni binarni prefiksni kod. Reči binarnog koda su nizovi bitova (ne obavezno fiksne dužine). Reči prefiksnog koda imaju svojstvo da niti jedna reč nije prefiks druge. Ako je neki kompresioni kod prefiksni, ta osobina je značajna zbog postupka dekompresije.

Hofmanovo kodiranje danas se često koristi kao "back-end" faza za druge kompresione metode kao na primer PKZIP algoritam DEFLATE. JPEG i MP3 algoritmi imaju front-end prolaz i kvantizaciju koju prati Hofmanovo kodiranje.

Kod Hofmanovog algoritma kreiraju se simboli promenljive dužine koji zamenjuju ulazne simbole. Što je verovatnoća pojavljivanja simbola veća, utoliko je manji broj bita kojim se on reprezentuje. Za jedinstveno identifikovanje simbola promenljive dužine se koriste jedinstveni prefiksni atributi (biti).

Kodiranje/dekodiranje simbola se u Huffman-ovoj tehnici vrši na osnovu Huffman-ovog stabla. Simboli u stablu se nalaze organizovani prema verovatnoći pojavljivanja. Simboli sa većom verovatnoćom se nalaze bliže korenu stabla, dok se simboli sa najmanjom verovatnoćom dalje.

Huffman-ovo stablo je binarno stablo i gradi se od dna ka vrhu. Kreće se od listova stabla i progresivno se gradi sve do korena. Algoritam za generisnje stabla je jednostavan i elegantan. Prvo se formira niz simbola u obliku listova koji će se povezati u binarno stablo. Za svaki od simbola se vezuje težina koja opisuje njegovu verovatnoću pojavljivanja (što je težina veća, to je veća i verovatnoća).


Stablo se gradi kroz sledeće korake:

1. Pronalaze se dva slobodna čvora u nizu sa najmanjom vrednošću težina.

2. Kreira se nadređeni čvor za pronađene čvorove. Dodaje mu se težina jednaka zbiru težina njegovih podređenih čvorova.

3. Nadređeni čvor se dodaje u niz slobodnih čvorova a podređeni čvorovi se izvlače iz niza.

4. Putanji od nadređenog do jednog od podređenih čvorova se dodeljuje vrednost 0, dok se putanji do drugog čvora dodeljuje vrednost 1.

5. Prethodni koraci se ponavljaju sve dok u nizu slobodnih čvorova ne preostane samo jedan. Poslednji čvor je koren Huffman-ovog binarnog stabla.

Povodom osobine optimalnosti,važno je istaći i da je pokazano da je Hofmanovo kodiranje najefikasniji kompresioni metod u svojoj klasi, a to je klasa preslikavanja karaktera eksterne azbuke neke tekstualne kolekcije u bitove  za poznatu frekvenciju pojave svakog karaktera eksterne azbuke. Ako verovatnoća pojave svakog simbola ima uniformnu distribuciju, a broj simbola je stepen dvojke, Hofmanovo kodiranje je kodiranje binarnim blokovima(ASCII,…).



Varijacije Hofmanovog kodiranja

Adaptivno Hofmanovo kodiranje

Ova varijanta izračunava frekvencije objekata dinamički tokom pregleda tekućeg dokumenta. Radi se o jednoprolaznom algoritmu korisnom za realtime aplikacije. Ova varijanta Hofmanovog kodiranja je kasnije upotrebljena u familiji Lempel-Ziv algoritama.

n-arno Hofmanovo kodiranje

n -arno Hofmanovo algoritmi koristi {0, 1,..., n − 1} alfabet za kodiranje objekata i izgradnju n-arnog stabla.



Zadatak 1. Optimalnim binarnim prefiksnim kodom kodirati rečenicu: NA VRH BRDA VRBA MRDA

Skup karaktera S={N, A, _, V, R, H, B, D, M} (_ je stavljeno umesto znaka za razmak)

Ako kodiramo ravnomernim kodom,onda je dužina binarne reči koda svakog karaktera bar 4 bita.
Za rečenicu sa 21 karakterom je potrebno 4*21 = 84 bita
Upotrebom tradicionalnih 7-bitnih/8-bitnih kodova, dužina je:

7*21 =147 bitova

8*21 =168 bitova

Ali, Hofmanovim kodiranjem će se dobiti optimalna dužina: (pogledati poglavlje 5.5 o kompresiji podataka u knjizi M. Živković "Algoritmika")

Neka je fi broj pojava karaktera i u rečenici. Tada je:


A

blanko

R

B

V

D

N

M

H

fi

4

4

4

2

2

2

1

1

1

Spajaju se 2 po 2 najmanje tezine (kada postoji vise mogucnosti na proizvoljan nacin se bira jedna.


A

blanko

R

B

V

D

N

MH

fi

4

4

4

2

2

2

1

2


A

blanko

R

B

V

D

MHN

fi

4

4

4

2

2

2

3


A

blanko

R

B

VD

MHN

fi

4

4

4

2

4

3


A

blanko

R

BMHN

VD

fi

4

4

4

5

4


A

R

BMHN

VDblanko

fi

4

4

5

8


AR

BMHN

VDblanko

fi

8

5

8


AR

BMHNVDblanko

fi

8

13


ARBMHNVDblanko

fi

21

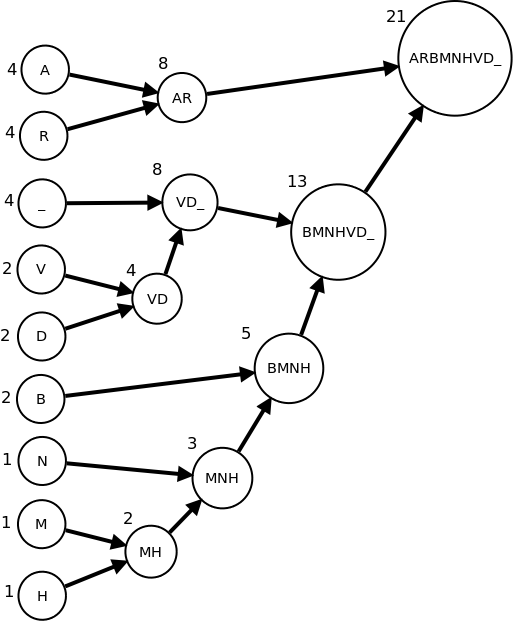
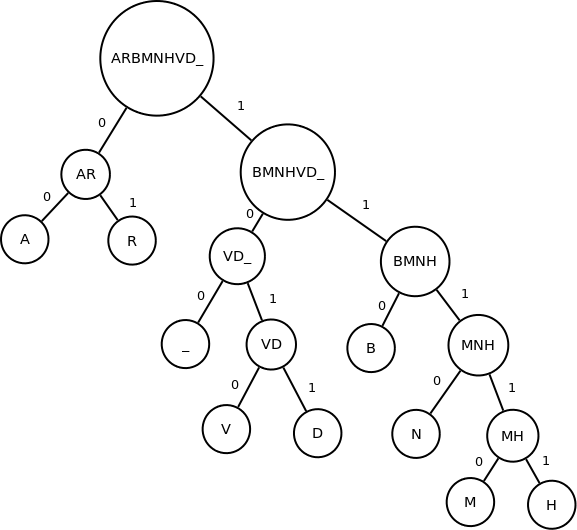
Prethodni postupak se moze prikazati i na sledeci nacin:



Konacno, rotacijom i dodavanjem 0 i 1 dobija se Hofmanovo stablo:

Dakle,tablica kodova glasi:

karakter

A

R

_

V

D

B

N

M

H

kod

00

01

100

1010

1011

110

1110

11110

11111

Broj bitova za rečenicu je:
f1*l1 + . . . + f9*l9= 2*4 + . . . + 5*1 = 64

Napomena: Hofmanovo kodiranje nije jednoznacno. U zavisnosti od toga koja se dva slobodna cvora izaberu dobija se razlicito stablo a time i razliciti kodovi.

ZADACI ZA VEZBU:

Zadatak 1. Optimalnim binarnim prefiksnim kodom kodirati rečenicu: RIBA RIBI GRIZE REP

Zadatak 2. Optimalnim binarnim prefiksnim kodom kodirati rečenicu: PO JUTRU SE DAN POZNAJE

Zadatak 3. Optimalnim binarnim prefiksnim kodom kodirati rečenicu: BEZ MUKE NEMA NAUKE

Zadatak 4. Optimalnim binarnim prefiksnim kodom kodirati rečenicu: BEZ ALATA NEMA ZANATA. Ako postoji vise od 2 cvora koji su iste tezine prvo spajati one koji imaju tekst sto je krace duzine, a ako ih ima vise od 2 sa tekstom istih duzina uzimati one sa pocetnim slovom blizim pocetku azbuke.

Uputstvo: dobijaju se novi cvorovi: BL, EM, NT, BLZ, _EM, BLZNT, _EMA, svi.


Grejov kod(Frank Grey)

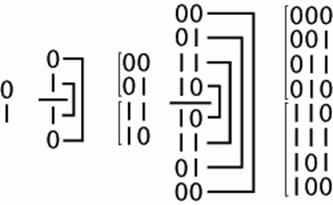
Grejov kod dužine n>1 je niz k-torki bita (k>=1) b1, b2,...bn takvih da se u nizu b svaka dva uzastopna člana, kao i prvi i poslednji član razlikuju na tačno jednoj poziciji. Na primer, Grejov kod dužine 4 je 00, 01, 11, 10.

Grejov kod se koristi i kao ciklički kod za kodiranje dekadnih cifara binarnim rečima sa svojstvom da pri prelasku sa dekadne cifre i nacifru i+1 u kodnoj reči se menja samo binarna cifra na jednoj poziciji. Ovo svojstvo ga čini pogodnim za primene u kontroli pozicija rotirajućih elemenata, na primer kod nekih štampača, mehaničkih dekodera, ...

Na primer Grejov kod za k=3, n=8

0 000

1 001

2 011

3 010

4 110

5 111

6 101

7 100

Izgradnja Grej koda sa k bita na osnovu k-1 bitnog Grej koda – prefiksovanjem najpre sa k nula, a potom sa k jedinica



G1. Da li postoji Grejov kod neparne dužine?

O1. Ne postoji, jer za i>1 b1,bi se razlikuju na parnom (neparnom) broju pozicija ako i je neparno(parno). Ako bi dužina koda n bila neparna, onda bi se b1,bn razlikovali na parnom broju pozicija, što je kontradikcija sa svojstvom da se oni razlikuju na jednoj poziciji.



Čekajući Godoa: Beckett-Gray kod

Interesantna primena Grejovog koda jeBeckett-Gray kod nazvanog po engleskom piscu Semjuelu Beketu. Sam Beket je kao režiser ekstremno poštovao principe simetrije na sceni u smislu da mu je bilo važan broj glumaca na i van scene.

Jedan od njegovih komada "Blok"se odigrava u 16 vremenskih perioda. Na kraju svakog perioda, Beket je želeo da jedan od četvoro glumaca ili uđe na ili iziđe sa scene i da komad započne i završi se sa praznom pozornicom.

Insistirao je i da se svaka grupa glumaca pojavi u zajedničkoj sceni najviše jednom.

Matematički formulisano, to znači da se glumci na pozornici mogu predstaviti 4-bit binarnim Grejovim kodom. Dodatno ograničenje Beketovog scenarija je bilo i da glumci izlaze na i odlaze sa pozornice tako da odlazi sa scene onaj glumac koji je najduže boravio na pozornici.

Dakle, glumci bi mogli da se reprezentuje FIFO strukturom reda čekanja, tako da prvi izlazni glumac bude onaj koji je i prvi ušao u red čekanja.

Inače, matematičimarima nije bilo jednostavno pokazati da li postoji ili neBeckett-Gray kod za n = 4, već je iscrpnom pretragom prostora rešenja utvrđeno da takav kod ne postoji, tj. Beket nije mogao ostvariti pređašnju zamisao, ali sa drugim brojem glumaca, moguće je. Jer za n = {2, 5, 6} postoji SB kod, ali ne postoji za n = {3, 4}.Interesantno je da prostor za pretragu rešenja za n = 6 je veliki i još nije kompletno okončana diskusija svih postojećih rešenja,već je poznatao nekoliko hiljada SB kodova za n = 6.



ZADACI ZA VEZBU:

Zadatak 1: Konstruisite 5-bitni Grejov kod.

Zadatak 2. Neka su A i B kvadratne matrice reda n cije su vrste otvoreni Grejovi kodovi (elementi su im iz skupa {0, 1}, a svake dve uzastopne vrste razlikuju se na tacno jednom mestu). Konstruisati algoritam slozenosti O(n2) za mnozenje ovakvih matrica.