3.
Ako je neka duž podeljena neprekidno, biće kvadrat zbira manjeg dela i polovine većeg dela pet puta veći od kvadrata na polovini većeg dela.
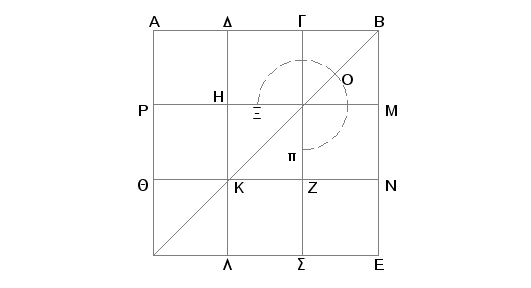
Neka je duž AB podeljena tačkom G neprekidno, i neka je veći deo AG, i AG prepolovljeno tačkom D. Tvrdim da je kvadrat na BD pet puta veći od kvadrata na DG.
Zaista, konstruišimo na AB kvadrat AE i nacrtajmo dvostruku sliku. Pošto je AG dvostruko DG, biće kvadrat na AG četiri puta veći od kvadrata na DG, tj. PS od ZH. I pošto je pravougaonik obuhvaćen od AB i BG jednak kvadratu na AG, a isti pravougaonik, obuhvaćen od AB i BG, jednak i GE, biće GE jednako PS. No PS je četvorostruko ZH. Dakle, i GE je četvorostruko ZH. Dalje, pošto je AD jednako DG, biće i QK jednako KZ. Te prema tome je i kvadrat HZ jednak kvadratu QL. A kako je HK jednako KL, a i MN - NE, biće i MZ jednako ZE. Ali MZ je jednako GH, pa prema tome je i GH jednako ZE. Dodajmo im isto GN; tada će gnomon XOp biti jednak GE. Ali već je dokazano da je GE četvorostruko HZ. I prema tome je i gnomon XOp četvorostruki kvadrat ZH. Znači, zbir gnomona XOp i kvadrata ZH je petostuki kvadrat ZH. No zbir gnomona XOp i kvadrat ZH je DN. A DN je kvadrat na DB, a HZ kvadrat na DG. Na ovaj način kvadrat na DB je petostruki kvadrat na DG. A to je trebalo dokazati.