Lema

Da ugao jednakostranog i jednakouglog petougla iznosi prav ugao i petinu pravog, dokazuje se ovako.

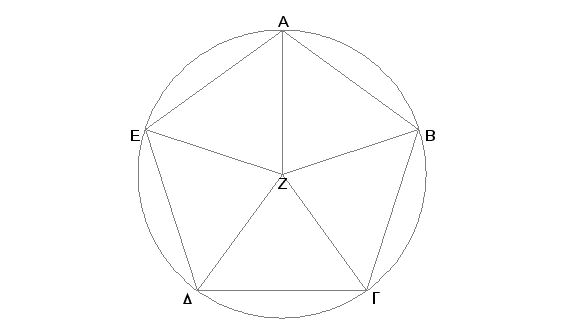
Neka je ABGDE jednakostrani i jednakougli petougao; opišimo oko njega krug ABGDE; uzmimo mu centar Z i spojimo ZA, ZB, ZG, ZD, ZE. Ove prave polove uglove kod A, B, G, D, E. Pošto je pet uglova kod Z jednako četiri prava ugla i oni su jednaki, jedan od njih, napr. AZB, iznosi prav ugao bez jedne petine pravog. A zbir ostala dva, ZAB i ABZ, iznosi prav ugao i jednu petinu. Kako je ugao ZAB jednak ZBG, biće i ceo ugao ABG jednak pravom uglu i jednoj petini. A to je trebalo dokazati.