1.
Jedan deo prave linije ne može se nalaziti u nekoj, osnovnoj, ravni, a drugi deo biti izdignut iznad te ravni.
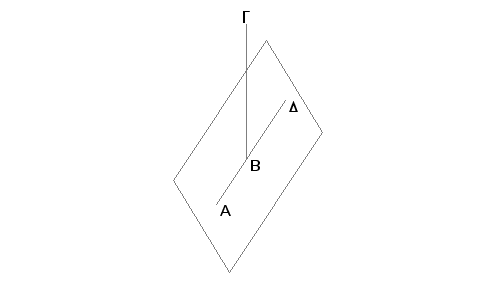
Zaista, ako je to moguće, neka se deo AB prave linije ABG nalazi u osnovnoj ravni, dok je drugi deo BG izdignut.
Neka postoji u osnovnoj ravni neka prava kao pravolinijsko produženje prave AB. Neka to bude BD. Na ovaj način AB je zajednički deo dve prave ABG i ABD. A to je nemoguće, jer, ako oko centra B sa poluprečnikom AB nacrtamo krug, njegovi prečnici otsecaće od kruga nejednake kružne lukove.
Na ovaj način, ne može se jedan deo prave linije nalaziti u nekoj, osnovnoj, ravni, a drugi biti izdignut iznad te ravni.
A to je trebalo dokazati.