36.

Ako se uzme ma koliko proporcionalnih brojeva sa jedinicom na prvom mestu u razmeri jedan prem dva i to dotle dok zbir svih tih brojeva ne postane prost broj i ako taj zbir pomnožen poslednjim brojem proizvodi nešto, biće dobiveni broj savršen.

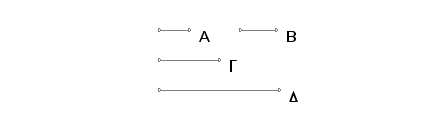
Uzmimo sa jedinicom na prvom mestu ma koliko proporcionalnih brojeva A, B, G, D sa razmerom jedan prema dva, i neka njihov zbir, broj E bude prost, i E pomnoženo sa D proizvodi broj ZH. Tvrdim da je ZH savršen broj.
Zaista, ma kolika bila množina brojeva A, B, G, D, toliko uzmimo brojeva E, QK, A, M koji su u neprekidnoj razmeri jedan prema dva. Tada na osnovu jednakoudaljenosti imamo da je A prema D kao E prema M. Dakle, proizvod od E i D jednak je prizvodu od A i M. A ako je proizvod od E i D jednak ZH, biće i proizvod od A i M jednak ZH. Dakle, A pomnoženo sa M proizvodi HZ. Prema tome M meri ZH prema broju jedinica u A. Ali A je dvojka, paje, znači, ZH udvostručen broj M. Međutim, i svaki od M, L, QK, E je dvaput veći od narednog. Na taj način su brojevi E, QK, L, M, ZH neprekidno proporcionalni u razmeri jedan prema dva. Oduzmimo sad od drugog QK i od poslednjeg ZH brojeve QN, odnosno ZX, svaki jednak prvom E.

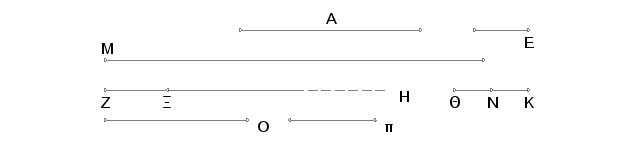
Tada, pošto se razlika drugog i prvog odnosi prema prvom kao razlika poslednjeg i prvog prema zbiru svih ispred njega, broj NK je prema E kao XH prema zbiru M, L, KQ, E. Ali, NKje jednako E, pa, znači, XH je jednako zbiru M, L, QK, E. Ali i ZX je jednako E, a E je jednako zbiru A, B, G, D i jedinice. Na taj način celo ZH je jednako zbiru E, QK, L, M sa zbirom A, B, G, D i jedinicom. I ono se meri tim brojevima. Tvrdim da se ZH ne meri nikakvim drugim brojevima sem A, B, G, D, E, QK, L, M i jedinicom. Zaista, neka se ZH meri, ako je moguće, brojem O i broj O nije isti ni sa jednim od brojevaA, B, G, D, E, QK, L, M. I neka koliko puta O meri ZH, toliko bude jedinica u p, tj. p pomnoženo sa O proizvodi ZH. Ali i E pomnoženo sa D proizvodi ZH. Dakle, i E je prema p kao O prema D. I pošto su, počev od jedinice, brojevi A, B, G, D neprekidno proporcionalni, D se neće meriti nikakvim drugim brojem sem brojevva A, B, G. Ali predpostavljeno je da O nije isti broj ni sa jednim od brojeva A, B, G. Znači O ne meri D. Ali je O prema D kao E prema p, znači, i E ne meri p. I pri tome je E prost broj. A svaki prost broj je sa svakim brojem, kojeg ne meri, uzajamno prost. Znači, brojevi E i p su uzajamno prosti. Ali prosti brojevi su i najmanji, a najmanji brojevi mere isti broj puta brojeve koji su sa njima u istoj razmeri i to predhodni meri predhodni i naredni - naredni. I pošto se E prema p odnosi kao O prema D, onda će E meriti isti broj puta O kao što i p meri D. Ali D se ne meri nikakvim drugim brojem sem A, B, G. Znači, broj p je isti sa jednim od brojeva A, B, G. Neka to bude broj B. I ma kolika bila množina brojeva B, G, D isto toliko brojeva uzmimo počev od E, naime E, QK, L. I neka ti brojevi E, QK, L budu u istoj razmeri sa brojevima B, G, D. Tada će po jednakoudaljenosti B biti prema D kao E prema L. Međutim, proizvod od B i E je jednak proizvodu od p i O. Ali proizvod od p i O jednak je proizvodu od B i L. Znači, proizvod od B i L jednak je proizvodu od D i L. Znači p je prema B kao kao L prema O. I p je isto Što i B, pa znači i L je isto što je i O. Ato je nemoguće, jer se pretpostavlja da O nije isto ni da jednim od uzetih brojeva. Znači ZH se ne meri nijednim od brojeva A, B, G, D, E, QK, L, M i jedinice. A dokazano je da je broj ZH jednak zbiru brojeva A, B, G, D, E, QK, L, M i jedinice. A savršen je onaj broj koji je jednak zbiru svih svojih delova (koji ga mere). Na ovaj način ZH je savršen broj. A to je trebalo dokazati.