35.

Ako postoji ma koliko neprekidno proporcionalnih brojeva pa se od drugog i poslednjeg oduzme isti broj jednak prvom broju, ostatak od drugog odnosi se prema prvom broju kao ostatak od poslednjeg prema zbiru svih ispred njega.

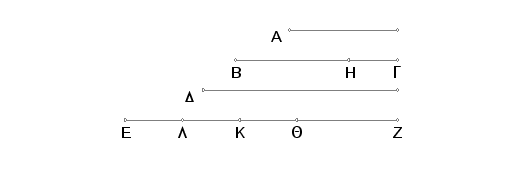
Neka postoji ma koliko neprekidno proporcionalnih brojeva A, BG, D, EZ, počev od najmanjeg A i neka se od BG i EZ oduzme BH, odnosno ZQ, svako jednako A. Tvrdim da je HG prema A kao EQ prema zbiru od A, BG, D.
Zaista, odmerimo ZKjednako BG i ZA jednako D. Pošto je ZK jednako BG, a ZQ jednako BH, biće i ostatak QK jednak ostatku HG. I pošto je EZ prema D kao D prema BG i kao BG prema A, a D je jednako ZA, i BG broju ZK, i A broju ZQ. Posle razdvajanja EA će se odnositi prema AZ kao AK prema Zk i kao AQ prema ZQ. Ali je jedan od predhodnih prema jednom od narednih kao zbir svih predhodnih prema zbiru svih narednih. Dakle, KQje prema ZQ kao zbir od EA, AK, KQ prema zbiru AZ, ZK, QZ. Ali , KQ je jednako GH, ZQ jednakO A, zbir AZ ZK, QZ zbiru D, BG, A. Prema tome je GH prema A kao EQ prema zbiru D, BG, A. Na ovaj način, ostatak od drugog posle oduzimanja prvog se odnosi prema prvom kao ostatak od poslednjeg posle oduzimanja prvog prema zbiru svih ispred poslednjeg. A to je trebalo dokazati.