31.
Ako je neparanbroj sa nekim brojem uzajamno prost, biće on uzajamno prost i sa dvostrukim tim brojem.
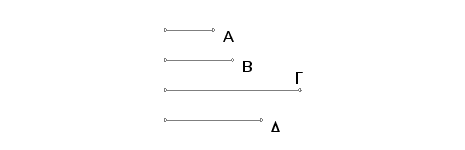
Neka je neparan broj A uzajamno prost sa nekim brojem B i G je dvostruki broj B. Tvrdim da je A uzajamno prost sa G.
Zaista, ako oni (A i B) nisu uzajamno prosti, tada ih meri isti broj. Neka ih meri, i neka to bude broj D. Ali, A je neparan broj, pa je tada i D neparan broj. I pošto D, neparan broj meri G, a G je paran broj, onda D meri i polovinu G. Ali polovina B je G, pa, znači, D meri B. A D meri i A. Prema tome D meri A i B koji su uzajamno prosti, a to je nemoguće. Znači, A i G nisu uzajamno složeni. Dakle, A i G su uzajamno prosti. A to je trebalo dokazati.