Ako su između dva broja umetnuti brojevi, koji su u neprekidnoj proporciji sa njima, onda će se između dva druga broja, koji su u istoj razmeri sa prvima moći umetnuti isti toliki broj neprekidno proporcionalnih brojeva.

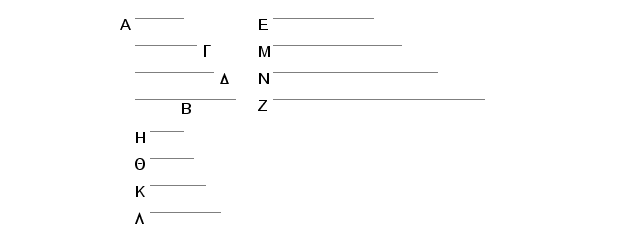
Neka su između dva broja A i B umetnuti brojevi G i D koji su u neprekidnoj proporciji sa njima, i neka je A prema B kao E prema Z. Tvrdim, da će se isto onoliko brojeva koliko je u neprekidnoj proporciji umetnuto između brojeva A i B, moći umetnuti neprekidno proporcionalnih brojeva i između E i Z.
Zaista, koliko je po količini brojeva A, B, G, D uzmimo toliko najmanjih brojeva H, Q, K, L koji su u istoj razmeri sa brojevima A, B, G, D. Tada su krajnji H i L uzajamno prosti. I pošto su brojevi A, B, G, D u istoj razmeri sa brojevima H, Q, K i L a i količina brojeva A, B, G, D jednaka je količini brojeva H, Q, K i L biće, prema jednakoudaljenosti, A prema B kao H prema L. Ali je A prema B kao E prema Z, te je i H prema L kao E prema Z. No, H i L su uzajamno prosti, a uzajamno prosti su i najmanji; prema tome, najmanji brojevi mere isti broj puta brojeve, koji su sa njima u istoj razmeri, veći meri veći i manji meri manji, tj. prethodni meri prethodni, a naredni - naredni. Prema tome, H meri E isti broj puta kao što L meri Z. A koliko puta H meri E toliko puta će svaki od Q i K meriti M i N. Znači, brojevi H, Q, K i L mere isti broj puta brojeve E, M, N, Z. I prema tome su brojevi H, Q, K, L u istoj razmeri sa brojevima E, M, N, Z. Ali, H, Q, K, L su u istoj razmeri sa brojevima A, G, D, B, pa prema tome su i brojevi A, G, D, B u istoj razmeri sa brojevima E, M, N, Z. Ali brojevi A, G, D, B su neprekidno proporcionalni, onda su i brojevi E, M, N, Z neprekidno proporcionalni. Te tako, koliko je brojeva u neprekidnoj proporciji umetnuto između brojeva A i B, isto toliki broj neprekidno proporcionalnih brojeva može se umetnuti i između E i Z. A to je i trebalo dokazati.