Za proizvoljan broj razmera datih u najmanjim brojevima naći najmanje neprekidno proporcionalne brojeve u datim razmerama.

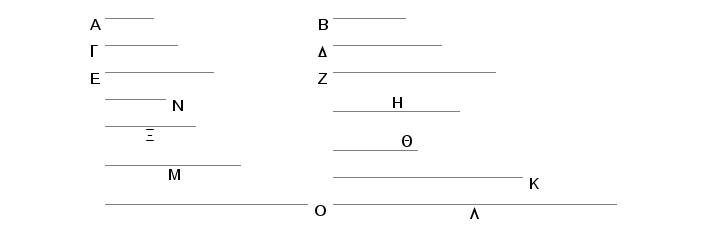
Neka su date razmere izražene najmanjim brojevima: A prema B, G prema D, i E prema Z. Treba naći najmanje brojeve u neprekidnoj proporciji u razmerama A prema B, G prema D, i E prema Z.
Uzmimo da je broj H najmanji zajednički multiplum brojeva B i G. I koliko puta B meri H, neka isto toliko puta i A meri Q; i koliko puta G meri H, neka isto toliko puta D meri K. Tada E ili meri K ili ne meri. Neka prvo E meri broj K i koliko puta E meri K, neka isto toliko puta i Z meri broj L. I, pošto, A meri Q isto toliko puta koliko B meri H, biće A prema B kao Q prema H. Iz istih razloga je i G prema D, kao H prema K, a i E prema Z kao K prema L. Prema tome, su brojevi Q, H, K i L neprekidno proporcionalni i u razmeri kao A prema B, kao G prema D, i kao E prema Z. Tvrdim da su oni i najmanji. Zaista, ako su brojevi Q, H, K, L neprekidno proporcionalni i u razmerama A prema B, G prema D i E prema Z, ali ne i najmanji, neka to onda budu brojevi N, X, M i O. Pošto je A prema B kao N prema X, a A i B su najmanji, i najmanji mere isti broj puta brojeve koji su u istoj razmeri sa njima, veći broj meri veći, a manji meri manji, tj. prethodni meri prethodni, a naredni - naredni, to A meri X. Iz istih razloga i G meri X. Prema tome, B i G mere X, znači i najmanji multiplum brojeva B i G meri X. Međutim, najmanji multiplum brojeva B i G je H; znači, i H meri X, veći broj meri manji, a to je nemoguće. Na taj način ne postoje neki brojevi manji od Q, H, K, L koji bi bili u razmerama A prema B, G prema D i E prema Z.

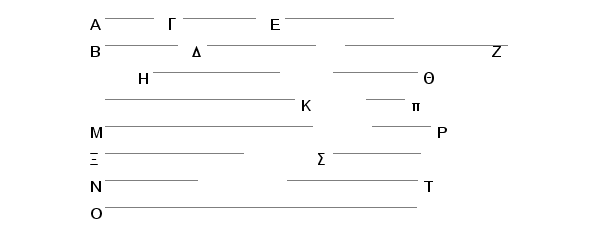
Neka sada E ne meri K. I neka je M najmanji multiplum brojeva E i K. I koliko puta K meri M, neka isto toliko puta svaki od brojeva Q, H meri svaki od brojeva N, X; a koliko puta E meri M neka toliko puta i Z meri O. Pošto Q meri N isto onoliko puta koliko H meri X, biće Q prema H kao N prema X. A ako je Q prema H, kao A prema B, biće A prema B, kao N prema X. Iz istih razloga i G je prema D kao X prema M. Sem toga, pošto E meri M isti broj puta kao što Z meri O, biće i E prema Z kao M prema O. Na ovaj način su brojevi N, X, M, O neprekidno proporcionalni i u razmerama: A prema B, G prema D i E prema Z. Tvrdim da su oni pri tome i najmanji u razmerama A prema B, G prema D, E prema Z. Ako nisu, onda postoje neki neprekidno proporcionalni brojevi u razmerama A prema B, G prema D, E prema Z, manji od brojeva N, X, M, O. Neka to budu brojevi p, P, S, T. I pošto je p prema P kao A prema B, a A prema B su najmanji, a najmanji mere brojeve koji su sa njima u istoj razmeri isti broj puta i to prethodni meri prethodni i naredni meri naredni, onda B meri P. Iz istih razloga i G meri P. Prema tome, B i G mere P, znači i najmanji multiplum brojeva B i G meri P. Ali, najmanji multiplum brojeva B i G jeste H, znači i H meri P. A pošto je H prema P kao K prema S, to K meri S. No i E meri S, znači E i K mere S. Međutim, tada i najmanji multiplum brojeva E i K meri S. Ali, najmanji multiplum brojeva E i K je M, te prema tome i M meri S, veći meri manji, a to je nemoguće. Prema tome, ne postoje neprekidno proporcionalni brojevi u razmerama A prema B, G prema D i E prema Z, koji bi bili manji od brojeva N, X, M, O. Na ovaj način su brojevi N, X, M, O najmanji neprekidno proporcionalni brojevi koji su u razmerama A prema B, G prema D, E prema Z. A to je i trebalo dokazati.