3.
Ako su neki brojevi, u proizvoljnom broju, neprekidno proporcionalni i oni su najmanji od brojeva koji su u istoj razmeri sa njima, onda su krajnji od njih uzajamno prosti.
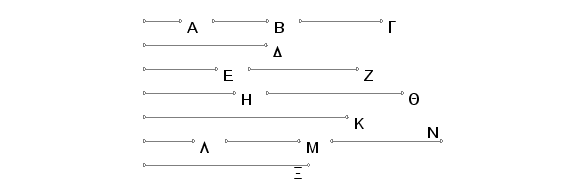
Neka su A, B, G, D neki neprekidno proporcionalni brojevi, i to najmanji od brojeva koji su u istoj razmeri sa njima. Tvrdim, da su krajnji od njih A i D uzajamno prosti.
Zaista, uzmimo dva najmanja broja, E, Z koji su u istoj razmeri sa brojevima A, B, G, D; zatim, uzmimo tri broja H, Q, K itd. dok uzeta količina brojeva ne bude jednaka količini brojeva A, B, G, D. Neka su oni uzeti i neka to budu brojevi L, M, N, X.
Pošto su E, Z najmanji od brojeva koji su u istoj razmeri sa njima, oni su uzajamno prosti. A ako svaki od brojeva E i Z množeći sam sebe proizvodi H i K, a množeći H i K proizvodi L, X to su H i K, pa i L i X, uzajamno prosti. No, pošto su A, B, G, D najmanji od brojeva koji su u istoj razmeri sa njima, a i L, M, N, X isto tako najmanji od brojeva koji su u istoj razmeri sa njima, i količina brojeva A, B, G, D je jednaka količini brojeva L, M, N i X to je svaki od brojeva A, B, G, D, jednako odgovarajućem broju od L, M, N, X. Pa prema tome, je A jednako L a D jednako X. No, L i X su uzajamno prosti pa su i A i D uzajamno prosti. A to je i trebalo dokazati.