25.
Ako su dva broja jedan prema drugom u razmeri kubnog broja prema kubnom i prvi broj je kub, onda je i drugi kub.
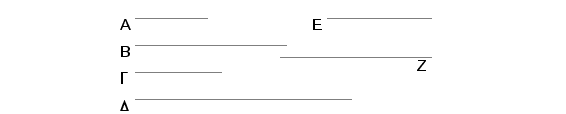
Neka su dva broja A i B jedan prema drugom u razmeri kubnog broja G prema kubnom broju D i broj A je kub. Tvrdim da je i B kub.
Zaista, pošto su G i D kubovi, G i D su slični zapreminski brojevi. Prema tome za G i D postoje dva srednje proporcionalna broja. Ali, onoliko koliko srednje proporcionalnih brojeva postoji između G i D, isto toliko postoji i između brojeva koji su u istoj razmeri sa njima. Na tj način i za brojeve A i B postoje dva srednje proporcionalna broja. Neka su umetnuti brojevi E i Z. Sad pošto su četiri broja A, E, Z, B neprekidno proporcionalni i A je kub, onda je i B kub. A to je trebalo dokazati.