Naći onoliko koliko se traži najmanjih neprekidno proporcionalnih brojeva koji su u datoj razmeri.

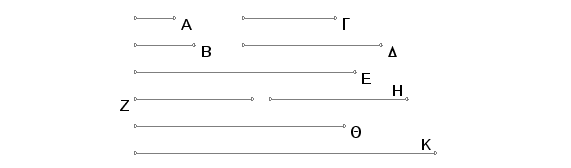
Neka je A prema B data razmera izražena pomoću najmanjih brojeva. Treba naći onoliko koliko se traži najmanjih neprekidno proporcionalnih brojeva, koji su u razmeri A prema B.
Neka se traži četiri broja i neka A pomnoženo samo sobom daje G, a pomnoženo brojem B proizvodi D. I neka B pomnoženo samo sobom daje E, a A pomnoženo brojevima G, D, E daje Z, H, Q i B pomnoženo brojem E daje K.
Pošto A pomnoženo samo sobom daje G, a pomnoženo brojem B daje D, biće A prema B kao G prema D. Dalje, pošto A pomnoženo brojem B proizvodi D, a pomnoženo samo sobom proizvodi E, to znači da brojevi A, B pomnoženi brojem B proizvode brojeve D odnosno E. Pa prema tome je A prema B kao i D prema E. Ali je A prema B kao i G prema D, znači G prema D je kao D prema E. Pošto A množeći G i D proizvodi Z i H, bić G prema D kao Z prema H. A ako je G prema D kao A prema B, biće i Z prema H kao A prema B. Pošto broj A množeći D i E proizvodi H i Q, biće D prema E kao i H prema Q. Ali je i D prema E kao A prema B. To je prema tome A prema B kao H prema Q. A pošto A i B pomnoženi sa E proizvode Q i K, biće A prema B kao i Q prema K. Ali je A prema B kao i Z prema H i kao H prema Q. I na taj način se Z odnosi prema H kao H prema Q i kao Q prema K. Znači, G, D, E i Z, H, Q, K su proporcionalni u odnosu A prema B. Tvrdim još da su oni i najmanji. Zaista, pošto su A i B najmanji od brojeva koji su u istoj razmeri sa njima, a najmanji od brojeva koji su u istoj razmeri sa njima uzajamno su prosti, biće i brojevi A i B uzajamno prosti. Iako brojevi A i B pomnoženi sami sobom proizvode odgovarajuće brojeve G i E, a pomnoženi na odgovarajući način brojevima G i E proizvode Z i K, onda su prema tome, G, E i Z, K uzajamno prosti. Ako su neki brojevi, u proizvoljnom broju, neprekidno proporcionalni i krajnji od njih uzajamno prosti, onda su to najmanji od brojeva koji su u istoj razmeri sa njima. Na ovaj način, brojevi G, D, E, i Z, H, Q, K su najmanji od brojeva koji su u istoj razmeri A prema B. A to je i trebalo dokazati.
Iz ovog je jasno da ako imamo tri broja u neprekidnoj proporciji najmanja od brojeva koji su u istoj razmeri, onda su krajnji brojevi kvadrati, a ako imamo četiri broja - krajnji brojevi su kubovi.