18.

Za dva slična površinska broja postoji srednje proporcionalan broj; i razmera površinskog broja prema sličnom površinskom broju je dva puta viša od razmere homolognih strana.

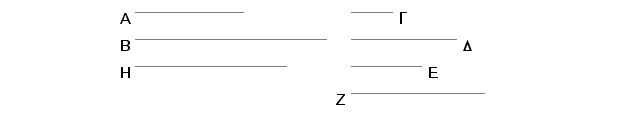
Neka su A i B dva slična površinska broja i neka su brojevi G i D strane broja A, a E i Z broja B. I pošto slični površinski brojevi imaju slične strane, biće G prema D kao E prema Z. Sada tvrdim, da za brojeve A i B postoji srednje proporcionalan broj i da je razmera A prema B dva puta viša od razmere G prema E ili od razmere D prema Z, tj. homologne strane prema homolognoj (strani).
Pošto je G prema D kao E prema Z, biće, posle permutovanja, G prema E kao D prema Z. I pošto su G i D strane površinskog broja A, onda D pomnoženo sa G daje A. Iz istih razloga i E pomnoženo sa Z daje B. Neka sad D pomnoženo sa E proizvodi H. I pošto D pomnoženo sa G proizvodi A, a pomnoženo sa E proizvodi H, biće G prema E kao A prema H. Ali, ako je G prema E kao D prema Z, biće i D prema Z kao A prema H. Zatim, pošto E pomnoženo sa D proizvodi H, a pomnoženo sa Z proizvodi B, biće D prema E kao H prema B. A dokazano je da je D prema Z kao A prema H. I prema tome je A prema H kao H prema B. Znači, brojevi A, H, B su neprekidno proporcionalni. Na ovaj način za brojeve A i B postoji srednje proporcionalni broj.
Tvrdim, da je razmera A prema B dva puta viša od razmere homologne strane prema homolognoj strani, tj. od razmere G prema E ili razmere D prema Z. Zaista, pošto su A, H, B neprekidno proporcionalni, razmera A prema B dva puta je viša od razmere A prema H. I, A je prema H kao G prema E, i kao D prema Z. Na ovaj način i razmere A prema B dva puta viša od razmere G prema E ili razmere D prema Z. A to je trebalo dokazati.