15.
Ako kubni broj meri kubni broj, onda ivica meri ivicu; i ako ivica meri ivicu, onda kub meri kub.
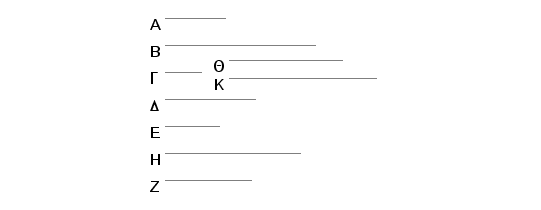
Neki kubni broj A meri kubni broj B, ivica broja A je G, i broja B je D. Tvrdim da G meri D.
Zaista, neka G pomnoženo samo sobom daje E, a D pomnoženo samo sobom daje H, i još G pomnoženo sa D daje Z, a svako od G i D pomnoženo sa Z daje Q odnosno K. Jasno je da su E, Z, H i A, Q, K, B neprekidno proporcionalni sa razmerom G prema D. I pošto su A, Q, K, B neprekidno proporcionalni, a A meri B onda A meri Q. A ako je A prema Q kao G prema D onda i G meri D.
Neka sad G meri D. Tvrdim da i A meri B.
Zaista, na osnovu istih rasuđivanja na sličan način se dokazuje da su A, Q, K, B neprekidno proporcionalni sa razmerom G prema D. I pošto G meri D, a G je prema D kao A prema Q, onda i A meri Q. Na ovaj način A meri i B. A to je trebalo dokazati.