12.
Za dva kubna broja postoje dva srednje proporcionalna broja i razmera kuba prema kubu je tri puta viša od razmere strane prema strani.
Neka su A i B dva kubna broja i strana A je G, a strana B je D. Tvrdim da za A i B postoje dva srednje proporcionalna broja i razmera A prema B je tri puta viša od razmere G prema D.
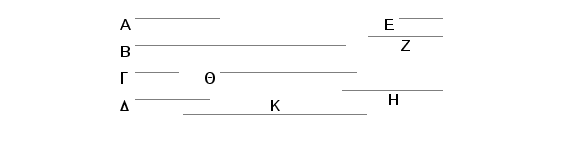
Zaista, neka G pomnoženo samu sobom daje E, pomnoženo sa D daje Z, a D pomnoženo sama sobom daje H, i Z, pomnoženo svakim od zvezdica G i D, proizvodi Q i K. Pošto je A kub, čija je strana G, i G pomnoženo samu sobom daje E, onda G pomnoženo samu sobom daje E, a pomnoženo sa E daje A. Iz istih razloga D pomnožena samo sobom daje H, a pomnoženo sa H daje B. I pošto G pomnoženo svakim od G i D daje E, odnosno Z biće G prema D kao E prema Z. Iz istih razloga je i G prema D kao Z prema H. Zatim, pošto G pomnoženo svakim od E i Z daje A, odnosno Q, biće E prema Z kao A prema Q. A ako je E prema Z kao G prema D, biće G prema D i kao A prema Q. Dalje, pošto svako G, D pomnoženo sa Z proizvodi Q odnosno K, biće G prema D kao Q prema K. Zatim, pošto D pomnoženo svakim od Z, H proizvodi K odnosno B, biće Z prema H, kao K prema B. A Z je prema H i kao G prema D. Na ovaj način, pošto je G prema D kao A prema Q i kao Q prema K i kao K prema B, to znači da za dva broja A i B postoje dva srednje proporcionalna broja Q i K.
Tvrdim još i da je razmera A prema B tri puta viša od razmere G prema D. Zaista, pošto su A, Q, K, B četiri neprekidna proporcionalna broja, biće razmera A prema B tri puta viša od razmere A prema Q. A ako je A prema Q kao G prema D, to je i razmera A prema B tri puta viša od razmere G prema D. A to je trebalo dokazati.